

初中数学人教版八年级上册第十二章 全等三角形12.3 角的平分线的性质一等奖ppt课件
展开角平分线的定义是什么?如何作出角平分线呢?
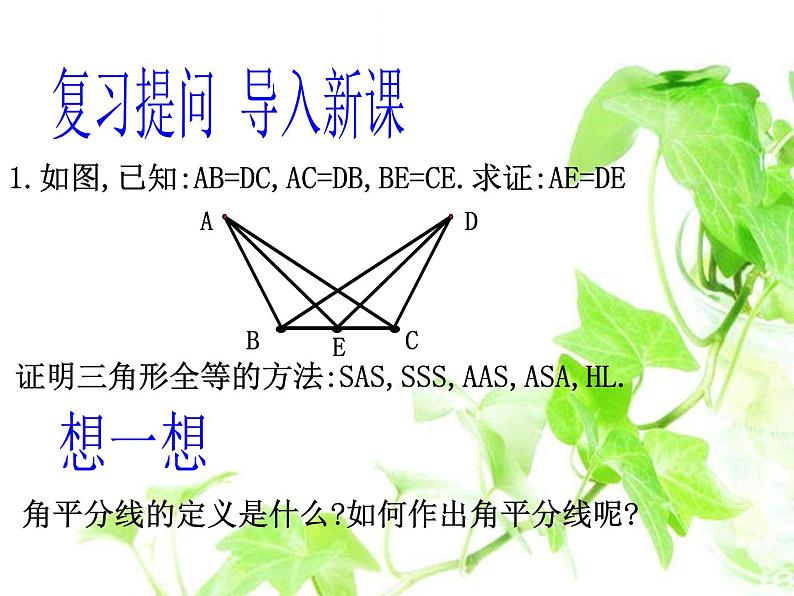
1.如图,已知:AB=DC,AC=DB,BE=CE.求证:AE=DE
证明三角形全等的方法:SAS,SSS,AAS,ASA,HL.
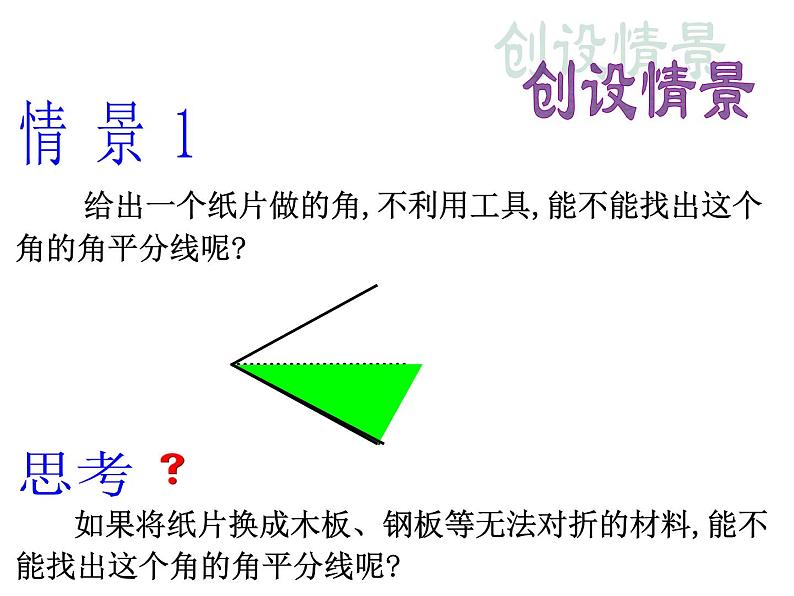
给出一个纸片做的角,不利用工具,能不能找出这个角的角平分线呢?
如果将纸片换成木板、钢板等无法对折的材料,能不能找出这个角的角平分线呢?
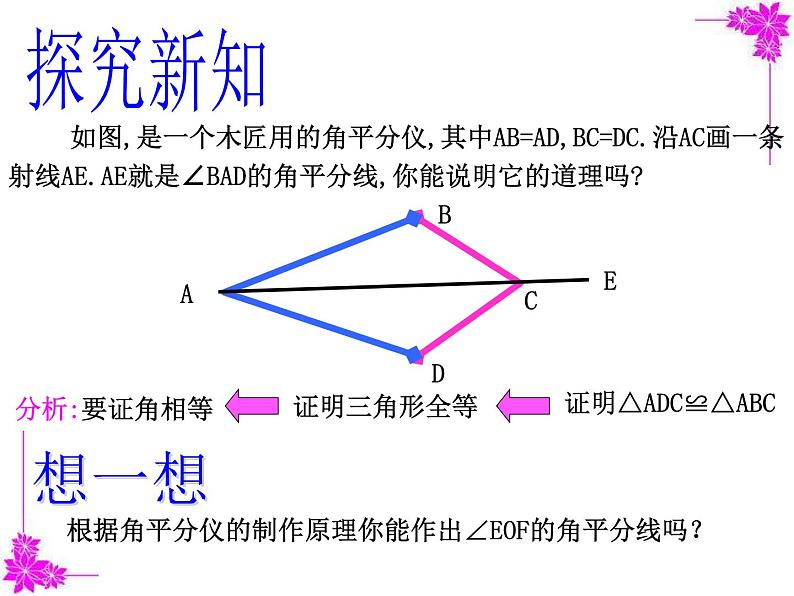
如图,是一个木匠用的角平分仪,其中AB=AD,BC=DC.沿AC画一条射线AE.AE就是∠BAD的角平分线,你能说明它的道理吗?
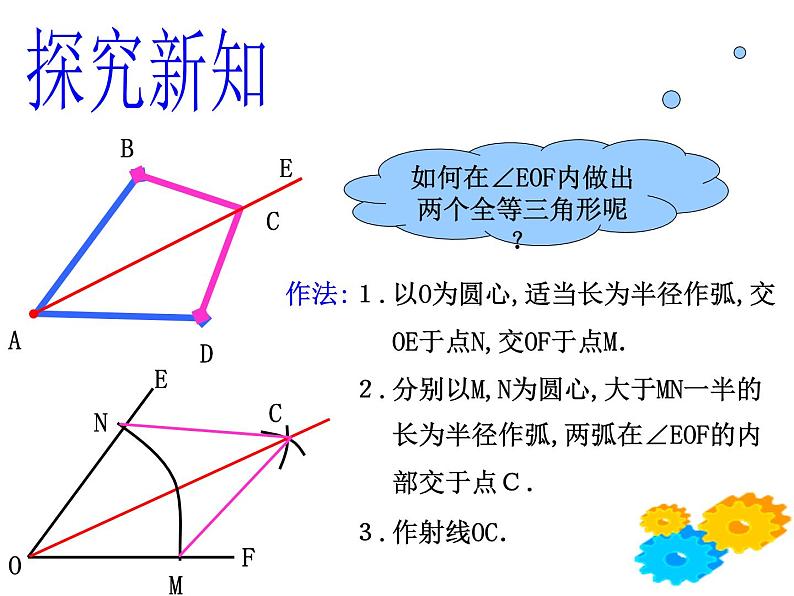
根据角平分仪的制作原理你能作出∠EOF的角平分线吗?
如何在∠EOF内做出两个全等三角形呢?
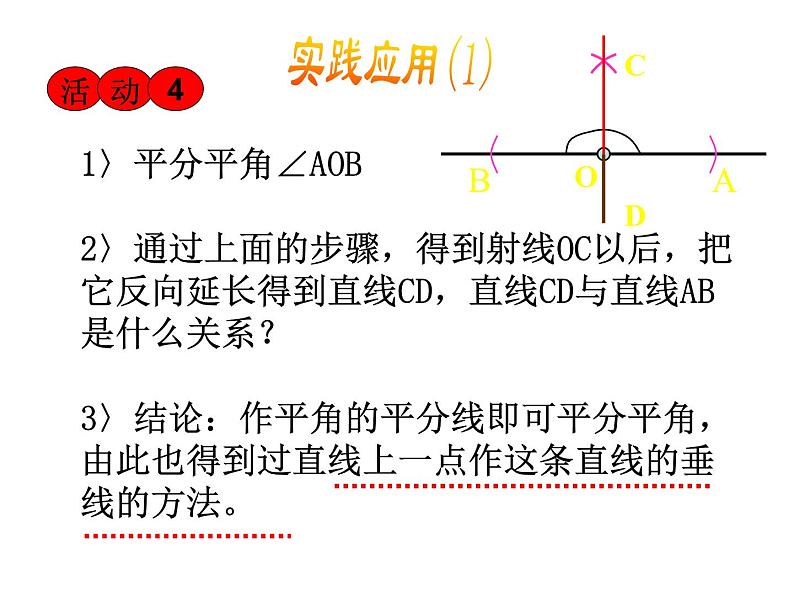
1〉平分平角∠AOB2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系? 3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
将∠AOB对折,在折痕上任取一点P,过P点再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
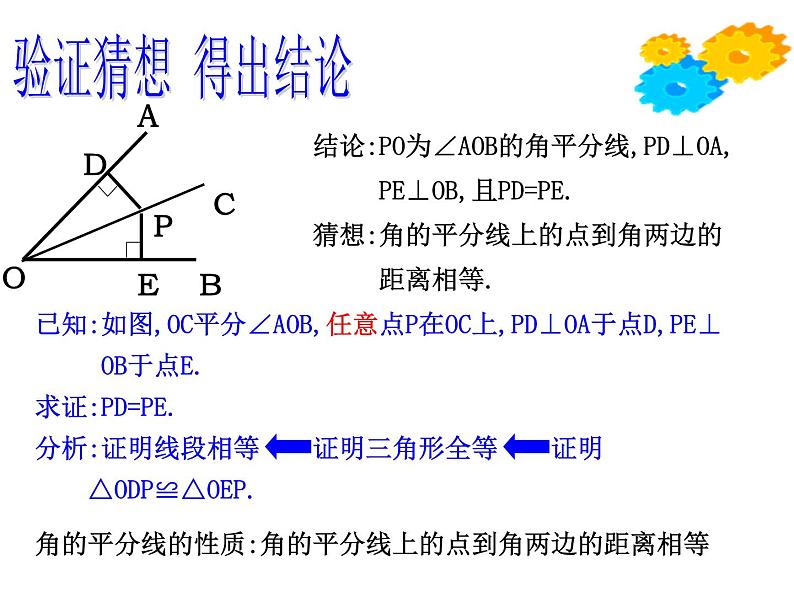
角的平分线的性质:角的平分线上的点到角两边的距离相等
结论:PO为∠AOB的角平分线,PD⊥OA, PE⊥OB,且PD=PE.猜想:角的平分线上的点到角两边的 距离相等.
证明一个几何中的命题时,要按照以下步骤:
1、明确命题中的已知和求证;2、根据题意,画出图形,并用数学符号表示已知和求证3、经过分析,找出由已知推出求证的途径,写出证明过程。
思考:要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)
∵PD⊥OA,PE⊥OB, 且PD=PE∴OP是∠AOB的平分线
在一个角的内部,到一个角的两边距离相等的点是否在这个角的平分线上?
角平分线性质的逆定理(角平分线的判定):在一个角的内部,到一个角的两边距离相等的点,在这个角的平分线上。
例1.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,且BE=CF。求证:AD是△ABC的角平分线。
证明:过点P作PD,PE,PF分别垂直于AB,BC,AC 于D,E,F. ∵ BM是△ABC的角平分线, 点P在BM上, ∴ PD=PE. 同理 PE=PF. ∴ PD=PE=PF.即点P到三边AB,BC,CA的距离相等.
例2.如图,△ABC的角平分线BM,CN相交于点P. 求证:点P到三边AB,BC,CA的距离相等.
例1.尺规作图,做下列角的角平分线.
1.如图,E是∠AOB的角平分线OC上的一点,EM⊥OB垂足为M, 且EM=3cm,求点E到OA的距离.
2.已知:如图,在△ABC中,AD是它的角平分线,且 BD=CD, DE⊥AB,DF⊥AC垂足分别是E,F. 求证:EB=FC.
1.如何做一个已知角的角平分线?2.角平分线的性质是什么?3.你会用角平分线的性质证明线段相等吗?
必做题:P110 T1 T2开放题:如图所示,AC,BC是公园的两道垂直的围墙,AD是公园里的一排树,AB是一条路,AD正好平分∠BAC,并且BC=10m,BD=6m,工作人员想从D点修一条路到达AB所在的路上,那么怎么修最近,要修多少米?
§13.3 角的平分线的性质复习引入 角平分线的做法 例题讲解 情景猜想 角平分线的性质 课堂小结
人教版八年级上册12.3 角的平分线的性质优秀课件ppt: 这是一份人教版八年级上册12.3 角的平分线的性质优秀课件ppt,共13页。PPT课件主要包含了学习目标,线段PC的长,高效预习,小组研习,证一证,说一说,反馈练习等内容,欢迎下载使用。
人教版12.3 角的平分线的性质精品课件ppt: 这是一份人教版12.3 角的平分线的性质精品课件ppt,共20页。PPT课件主要包含了情境问题,探究新知,实践应用1,3验证猜想,用数学语言表述,实践应用2,小结与作业,角平分线的性质等内容,欢迎下载使用。
初中数学人教版八年级上册12.3 角的平分线的性质优质课ppt课件: 这是一份初中数学人教版八年级上册12.3 角的平分线的性质优质课ppt课件,共30页。PPT课件主要包含了知识回顾,定义重合法,SSS,SAS,ASA,AAS,尺规作角的平分线,说一说,角平分线的性质,不必再证全等等内容,欢迎下载使用。













