数学沪科版20.2 数据的集中趋势与离散程度获奖课件ppt

这是一份数学沪科版20.2 数据的集中趋势与离散程度获奖课件ppt，共35页。PPT课件主要包含了本节课你有什么收获等内容，欢迎下载使用。

绘制频数分布直方图的一般步骤：
并把第一组的起点定为比最小的数据稍小一点的数.
一般地把表示分点的数比原数据多取一位小数，
绘出相应的长方形条，
纵轴表示频数，
(1) 计算这批数据中最大数和最小数的差.
(2) 决定组距和组数
每个小组的两个端点间的距离.
称为这个组的频数。
我们把一批数据中
落在某个小组内数据的个数
画出相互垂直的两条直线，
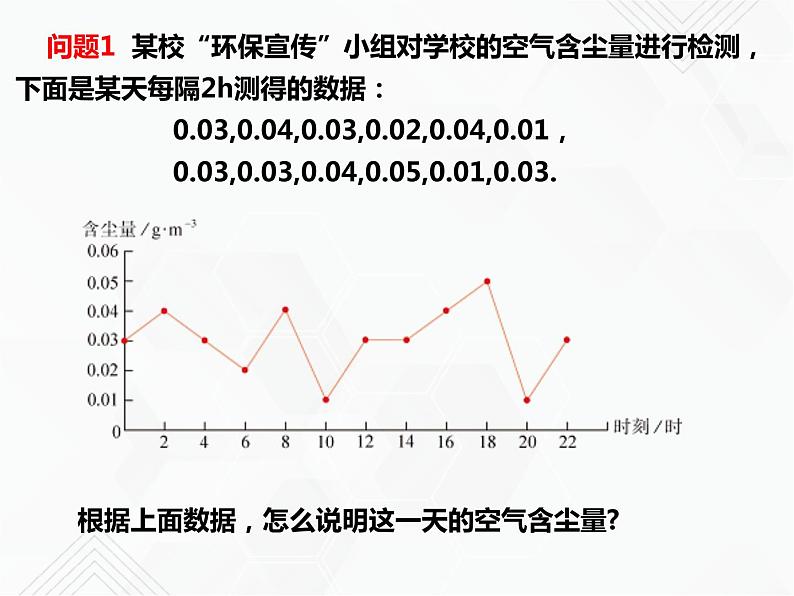
根据上面数据，怎么说明这一天的空气含尘量?
问题1 某校“环保宣传”小组对学校的空气含尘量进行检测，下面是某天每隔2h测得的数据： 0.03,0.04,0.03,0.02,0.04,0.01， 0.03,0.03,0.04,0.05,0.01,0.03.
思考 在小学我们对平均数有所认识,你能简单的说出平均数的概念吗?
用来反映该日空气含尘量的一般状况.
计算上述数据的平均数：
×(0.03+0.04+0.03+0.02+0.04+0.01+0.03
+0.03+0.04+0.05+0.01+0.03)
我们说学校这一天的空气含尘量平均为0.03g/m3.
把这个平均数作为这组数据的一个代表，
所得的商，
简称平均数或均数.
来作为刻画它的集中趋势的一种方法；
一般的，如果有n个数据
x1，x2，x3，···，xn
（x1+x2+x3+···+xn）
就是这组数据的平均数，
用“ ”表示，
平均数是反映数据的平均水平的一个特征量.
一是将评委评分的平均数作为最后得分；
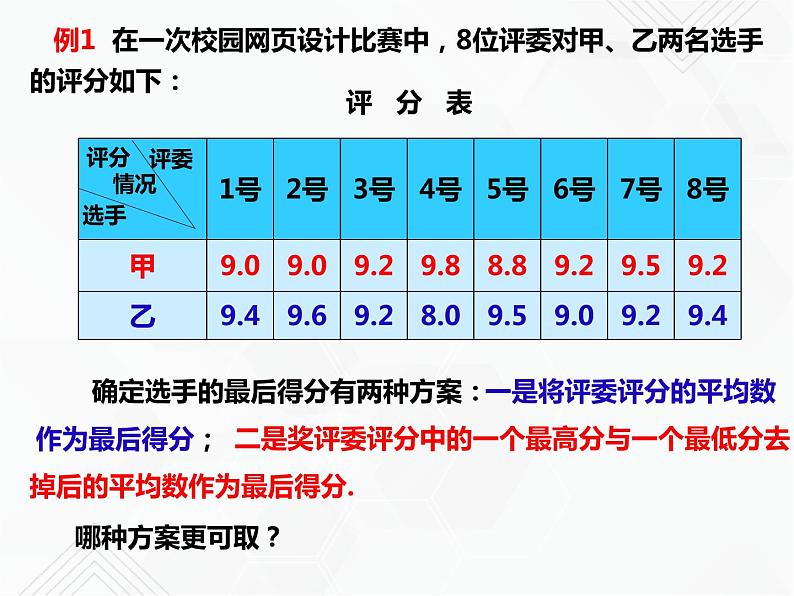
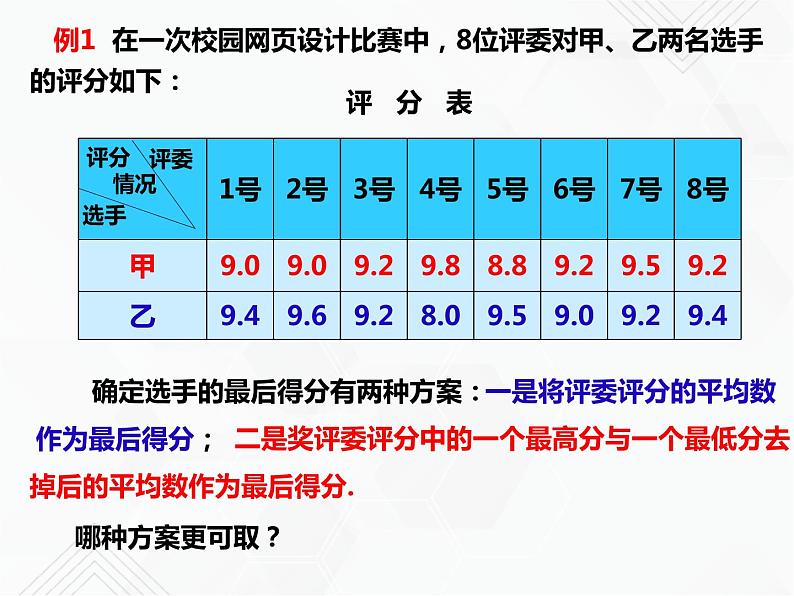
例1 在一次校园网页设计比赛中，8位评委对甲、乙两名选手的评分如下：
确定选手的最后得分有两种方案：
二是奖评委评分中的一个最高分与一个最低分去掉后的平均数作为最后得分.
当一组数据大部分都在某一常数a附近上下波动时，
（ ）
其中a表示各个数据中较“整”的数，
分别表示各个数据与a的差,
（8.8+9.0×2+9.2×3+9.5+9.8）
（8.0+9.0+9.2×2+9.4×2+9.5+9.6）
这时，甲的成绩比乙高.
按方案二计算甲、乙的最后得分为
（9.0×2+9.2×3+9.5）
（9.0+9.2×2+9.4×2+9.5）
这时，乙的成绩比甲高.
按方案一计算甲、乙的最后得分为
若这组数据中的一个数据变小，
如果这组数据中的一个数据变大，
我们发现有5位评委对甲的评分不高于乙，
将上面的得分与表中的数据相比较，
方案二的结果表明乙的成绩比甲的高，
这表明多数人认为乙的成绩比较好.
因此，方案二评定选手的最后得分比较可取.
与大多数评委的观点相符.
1、通过对上题的解决，你能说出平均数的大小与什么有关吗？
平均数的大小与一组数据的每个数据都有关系，
对应练习：个体户张某经营一家餐馆，下面是该餐馆所有工作人员200年10月份的工资：
张某： 4000元； 会计： 700元； 厨师甲：1000元
厨师乙： 900元； 杂工甲：580元； 杂工乙：560元
服务员甲：620元；服务员乙：600元；服务员丙：580元
(1) 计算他们的平均工资，这个平均工资能否反映餐馆加工在这个月收入的一般水平？
(2) 不计张某的工资，再求餐馆员工的月平均工资，这个平均工资能代表一般水平吗？
因为员工中工资最高的厨师甲的月收入1000元也小于这个平均数.
解：(1) 餐馆全体员工的月平均工资为
1060元不能代表餐馆员工在这个月的月收入的一般水平，
692.5元能代表餐馆员工在这个月的月收入的一般水平。
思考：通过这个问题，你能说出平均数有什么缺点吗？
(2) 员工的月平均工资为：
只计算余下的数据的平均数，
用平均数作为一组数据的代表，
想一想怎样避免这个缺点？
如某些评奖比赛的计分，通常去掉一个最高分和一个最低分.
容易受到个别极端数值的影响.
为了消除这种现象，可将少数极端数据去掉，
并把所得的结果作为全部数据的平均数.
例 2 某校在招聘新教师时以考评成绩确定人选. 甲、乙两位高校毕业生的各项考评成绩如下表：
(1) 如果学校将教学设计、课堂教学和答辩按1：3：1的比例来计算各人的考评成绩，那么谁会被录用?
90×1+85×3+90×1
80×1+92×3+83×1
(2)如果按教学设计占30%、课堂教学占50%、答辩占20%来计算各人的成绩，那么谁会被录用？
90×30%+85×50%+90×20%
80×30%+92×50%+83×20%
各个指标的重要程度不一样，考评的结果也就不同.
上例中是用什么来表示各个指标的重要程度？
(1)是用各项所占比例的形式来表示各个指标的重要程度的.
(2)是用各项所占百分比的形式来表示各个指标的重要程度的.
它们都是用来衡量各项考评成绩在总评分中所占权重”，“权重”不一样，结果就不一样.
这n个数据的加权平均数.
在总结果中的比重(如例2)，
一般地，对上面的求平均数，可统一用下面的公式：
我们称其为各数据的权，
其中f1，f2，f3，…，fk
x1，x2，x3，…，xk
出现的次数(如例1)，
表示数据x1，x2，x3，…，xk
通过例2，我们可以看出数据的权能反映数据的相对“重要程度”.
f1=1，f2=1，f3=1，…，fk=1时，
公式②和公式①有什么关系？
公式①是公式②的一种特殊形式，
（x1+x2+x3+········+xn）
2、若m个数的平均数为x，n个数的平均数为y，则这(m+n)个数的平均数是（ ）
1、某次考试，5名学生的平均分是82，除甲外，其余4名学生的平均分是80，那么甲的得分是（ ） A.84 B. 86 C. 88 D. 90
3、李大伯有一片果林，共有80棵果树．某日，李大伯开始采摘今年第一批成熟的果子，他随机选取2棵果树共摘得10个果子，质量分别为（单位：㎏）：0.28，0.26，0.24，0.23，0.25，0.24，0.26，0.26，0.25，0.23．以此估算，李大伯收获的这批果子的单个质量和总质量分别约为（　　） ㎏，200 ㎏ B.2.5 ㎏，100 ㎏ ㎏，100 ㎏ D.2.5 ㎏，200 ㎏
4、已知:x1,x2,x3,…, x10的平均数是a，x11,x12,x13,… ,x30的平均数是b，则x1,x2,x3,… ,x30的平均数（     ）
A.(a+b)   
5、若x1，x2，x3，···，xn的平均数为 ，则：
(1) nx1，nx2，nx3，···，nxn的平均数为 .
(2) x1+b，x2+b，x3+b，···，xn+b的平均数为 .
(3) nx1+b，nx2+b，nx3+b，···，nxn+b的平均数为 .
拓展练习： 若x1,x2,…, xn 的平均数为 ，y1,y2,…, yn 的平均数为 ，则 x1+y1，x2+y2，x3+y3，···，xn+yn 的平均数为 .
6.一家公司打算招聘一名英文翻译，对甲、乙两名应试者进行了听、说、读、写的英语水平测试，他们各项的成绩（百分制）如下：
如果这家公司想招一名口语能力较强的翻译，听、说、读、写成绩按照3：3：2：2的比确定，计算两名应试者的平均成绩(百分制).从他们的成绩看，应该录取谁？
85×3＋83×3＋78×2＋75×2 3＋3＋2＋2
73×3＋80×3＋85×2＋82×2 3＋3＋2＋2
显然甲的成绩比乙的高，所以从成绩看，应该录取甲．
听、说、读、写的成绩按照3：3：2：2的比确定.
7.一次演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分，各项成绩均按百分制，然后再按演讲内容占50％、演讲能力占40％、演讲效果占10％的比例，计算选手的综合成绩（百分制）．进入决赛的前两名选手的单项成绩如下表所示：
解：选手A的最后得分是
85×50％＋95×40％＋95×10％
95×50％＋85×40％＋95×10％
由上可知选手B获得第一名，选手A获得第二名．
8、小林、小红两位同学英语各单项测试成绩如下：
若听力、阅读、写作三项成绩分别按15％，50％，35％计入总分，谁的总成绩好？若分别按35％，50％，15％呢？
若按15％，50％，35％计入总分：
若按35％，50％，15％计入总分：
9.小明同学在初二年级第一学期的数学成绩如下表格, 请按图示的平时、期中、期末的权重，计算小明同学的学期总评成绩.
先计算小明的平时成绩:
(89+78+85)÷3
再计算小明的总评成绩:
84×10%+ 90×30%+ 87×60%
= 87.6 (分)
x1，x2，x3，···，xn表示各个数据.
其中n表示数据的总个数，
② 当一组数据大部分都在某一常数a附近上下波动时，
2、加权平均数计算方法：
一般地，对上面的加权平均数，可统一用下面的公式：
求一组数据的平均数，当数据很多时，用笔算比较麻烦，这是用计算器就很方面。只要按着指定的方法将各个数据依次输入计算器，即可直接得出结果。下面我们以例1中求选手甲的平均数为例加以说明.