初中数学沪科版八年级下册20.2 数据的集中趋势与离散程度优质ppt课件

这是一份初中数学沪科版八年级下册20.2 数据的集中趋势与离散程度优质ppt课件，共25页。PPT课件主要包含了问题引入，小明说谎了吗，合作探究，中位数与众数，分组讨论，中位数和众数的定义，和35，想一想，练一练，归纳总结等内容，欢迎下载使用。

1. 数学期中考试，小明同学得了 78 分. 全班共 30 人，其他同学的成绩为 1 个100 分， 4 个 90 分， 22 个 80 分，以及一个 2 分和一个 10 分. 小明回家告诉妈妈说，他这次成绩处于班级“中上水平”.
思考：小王回忆十年前大学毕业后找工作的经历，开始想找一份月薪在 1700 元以上的工作，那天他看见某公司门口的招聘广告，上面写着：现因业务需要招员工一名，有意者欢迎前来应聘，当时小王走了进去……
我们好几人工资都是 1800 元.
我公司员工的收入很高，月平均工资为 2700 元.
你们公司员工收入到底怎样呢？
我的工资是 1900 元，在公司中算中等收入.
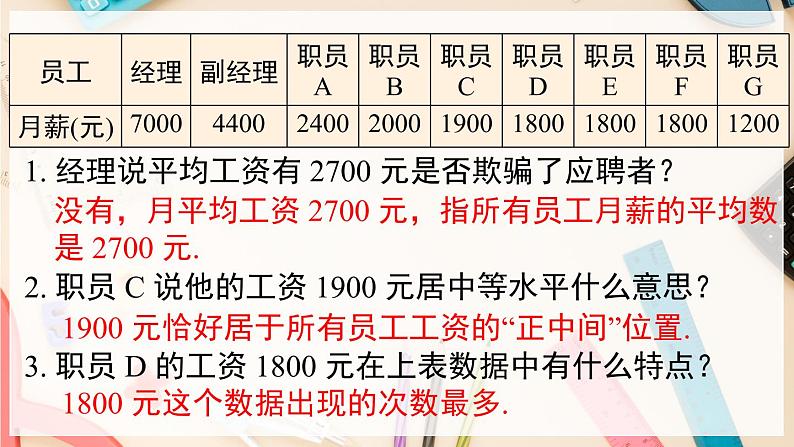
1. 经理说平均工资有 2700 元是否欺骗了应聘者？
2. 职员 C 说他的工资 1900 元居中等水平什么意思？
3. 职员 D 的工资 1800 元在上表数据中有什么特点？
没有，月平均工资 2700 元，指所有员工月薪的平均数是 2700 元.
1900 元恰好居于所有员工工资的“正中间”位置.
1800 元这个数据出现的次数最多.
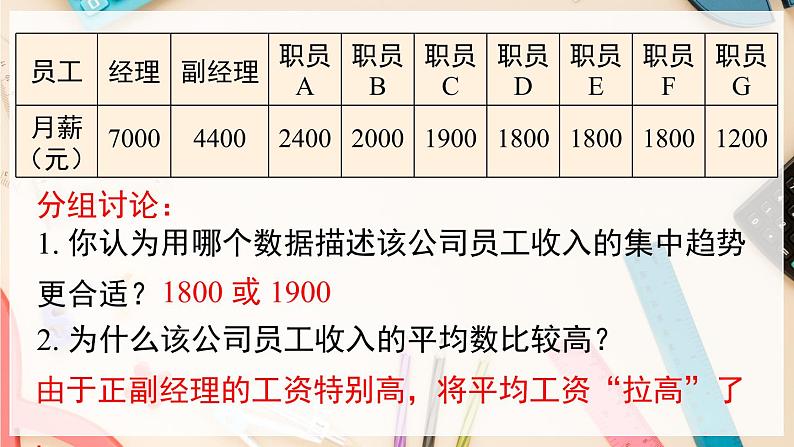
1. 你认为用哪个数据描述该公司员工收入的集中趋势更合适？2. 为什么该公司员工收入的平均数比较高？
由于正副经理的工资特别高，将平均工资“拉高”了.
1800 或 1900
一组数据中出现次数最多的数据叫做这组数据的众数.
一般地，当将一组数据按大小顺序排列后，位于正中间的一个数据（当数据的个数是奇数时）或正中间两个数据的平均数（当数据的个数是偶数时）叫做这组数据的中位数.
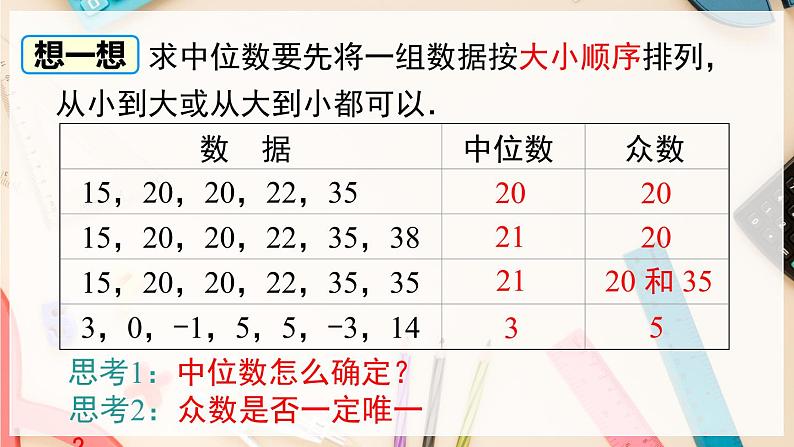
求中位数要先将一组数据按大小顺序排列，从小到大或从大到小都可以．
思考2：众数是否一定唯一？
思考1：中位数怎么确定？
将一组数据按照由小到大（或由大到小）的顺序排列： 如果数据的个数是奇数，那么位于正中间位置的数为这组数据的中位数； 如果数据的个数是偶数，那么正中间两个数据的平均数为这组数据的中位数．
如果一组数据中有极端数据，中位数比平均数更能合理地反映该组数据的整体水平．
思考：中位数有何意义？
下面两组数据的中位数是多少？
（1）5，6，2，3，2；
（2）5，6，2，4，3，5.
提示：确定中位数要先排序、看奇偶，再计算.
解：（1）中位数是 3.
（2）中位数是 4.5.
（1）一组数据中可能没有众数，如 1，2，3，4，6，5 中没有众数.
（2）一组数据的众数可能不止一个，如 1，1，2，3，3，5 中众数是 1 和 3.
（3）众数是一组数据中出现次数最多的数据而不是最多的次数，如 1，1，1，2，2，5 中众数是 1 而不是 3.
都反映数据的集中趋势，能从不同角度提供信息.
平均数、中位数和众数有哪些特征和优缺点?
平均数能充分利用数据提供的信息，它的使用最为广泛，能刻画一组数据整体的平均状态，但不能反映个体性质，易受极端值（即一组数据中与其余数据差异很大的数据）的影响.
中位数代表了这组数据数值大小的“中点”，不易受极端值影响，但不能充分利用所有数据的信息.
众数反映一组数据中出现次数最多的数据. 一组数据中，众数可能不止一个，也可能没有.
例1 在一次男子马拉松长跑比赛中，抽得 12 名选手所用的时间（单位：min）如下：136 140 129 180 124 154146 145 158 175 165 148（1）样本数据（12 名选手的成绩）的中位数是多少？
解：先将样本数据按照由小到大的顺序排列： __________________________________ __________________________________ 这组数据的中位数是__________________________的平均数，即答：样本数据的中位数是______min.
124129136140145146148154158165175180
处于中间的两个数 146 和 148
____________.
(2) 一名选手的成绩是 142 min，他的成绩如何？
(3) 由（1）知样本数据的中位数为______min，它的意义是：这次马拉松比赛中，大约有_________选手的成绩快于 147 min，有______选手的成绩慢于 147 min. 这名选手的成绩是 142 min，快于中位数________，因此可以推测他的成绩比__________选手的成绩好.
例2 已知一组数据 10，10，x，8 (由大到小排列) 的中位数与平均数相等，求 x 值及这组数据的中位数.
解：∵ 10，10，x，8 的中位数与平均数相等， ∴ (10 + x)÷2＝ (10 + 10 + x + 8)÷4. ∴ x＝8. (10 + x)÷2＝9. ∴ 这组数据的中位数是 9.
一组数据 18，22，15，13，x，7，它的中位数是 16，则 x 的值是_____.
分析：这组数据有 6 个，中位数是中间两个数的平均数. 因为 7 < 13 < 15 < 16 < 18 < 22，所以中间两个数必须是 15，x，故 (15 + x)÷2 = 17，即 x = 17.
例3 一家鞋店在一段时间内销售了某种女鞋 30 双，各种尺码鞋的销售量如表所示.你能根据表中的数据为这家鞋店提供进货建议码？
解：由上表看出，在鞋的尺码组成的数据中，_______是这组数据的众数，它的意义是：_______cm 的鞋销量最大. 因此可以建议鞋店多进_______cm 的鞋.
思考：你还能为鞋店进货提出哪些建议？
下面的扇形图描述了某种运动服的 S 号、M 号、L 号、XL 号、XXL 号在一家商场的销售情况. 请你为这家商场提出进货建议.
解：因为众数是 M 号，所以建议商场多进 M 号的运动服，其次是进 S 号，再其次进 L 号，少进 XXL号的运动服.
1. 某公司 56 名员工的月工资统计如下：求该公司员工月工资的平均数、中位数和众数.
解：平均数是 1000，
2. 若数据 80、81、79、68、75、78、x、82 的众数是 81，则（ ） A. x = 79 B. x = 80 C. x = 81 D. x = 823.“十•一”黄金周期间，某风景区在 7 天假期中每天上山旅游的人数统计如下表：其中中位数和众数分别是（ ） A.1.2，2 B.2，2.5 C.2，2 D.1.2，2.5
4. 某公司有 15 名员工，他们所在的部门及相应每人所创的年利润（万元/人·年）如下表所示：
根据表中提供的信息填空：1. 该公司每人所创年利润的平均数是( )万元，中位数是( )万元，众数是( )万元.2.你认为应该使用平均数还是中位数来描述该公司每人所创年利润的一般水平？
5. 某校男子足球队的年龄分布如下面的条形图所示. 请找出这些队员年龄的平均数、众数、中位数，并解释它们的意义.
分析：总的年龄除以总的人数就是平均数；出现次数最多的那个数，称为这组数据的众数；中位数一定要先排好顺序，然后再根据奇数或偶数个来确定中位数，若数据是奇数个，则正中间的数字即为所求；若是偶数个，则求中间两位数的平均数.
解：这些队员年龄的平均数是(13×2+14×6+15×8+16×3+17×2+18×1)÷22=15(岁)，众数是 15 岁，中位数是 15 岁.
意义：由平均数是 15 可说明队员们的平均年龄为 15 岁；由众数是 15 可说明大多数队员的年龄为 15 岁；由中位数是 15 可说明有一半队员的年龄大于或等于15岁，有一半队员的年龄小于或等于15岁.