初中数学人教版九年级下册27.2.2 相似三角形的性质优秀学案

这是一份初中数学人教版九年级下册27.2.2 相似三角形的性质优秀学案，共8页。学案主要包含了学习目标，要点梳理，典型例题，思路点拨，总结升华，答案与解析等内容，欢迎下载使用。




【学习目标】


1、探索相似三角形的性质，能运用性质进行有关计算；


2、通过典型实例认识现实生活中物体的相似，能运用图形相似的知识解决一些简单的实际问题（如何把实际问题抽象为数学问题）.


【要点梳理】


要点一、相似三角形的性质


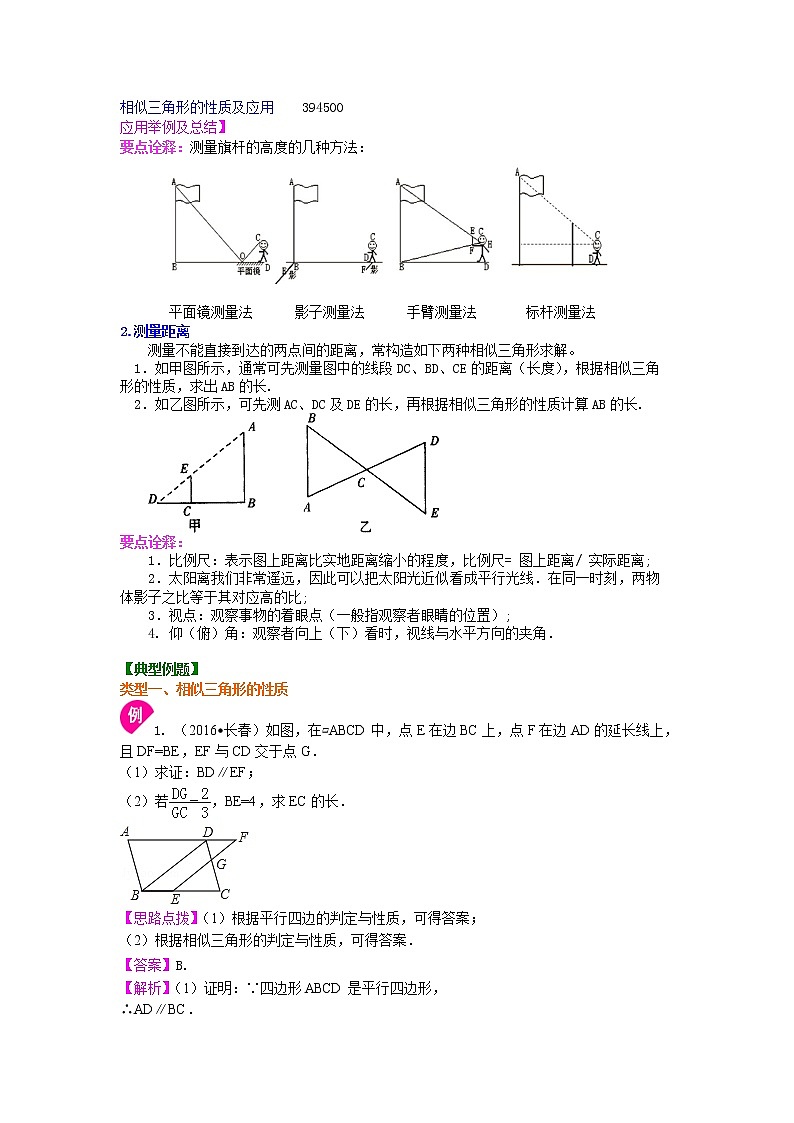
相似三角形的性质及应用 394500


相似形的性质】


1．相似三角形的对应角相等，对应边的比相等.


2. 相似三角形中的重要线段的比等于相似比.


相似三角形对应高，对应中线，对应角平分线的比都等于相似比.


要点诠释：要特别注意“对应”两个字，在应用时，要注意找准对应线段.


3. 相似三角形周长的比等于相似比


∽，则


由比例性质可得：





4. 相似三角形面积的比等于相似比的平方


∽，则分别作出与的高和，则























要点诠释：相似三角形的性质是通过比例线段的性质推证出来的.


要点二、相似三角形的应用


1.测量高度


测量不能到达顶部的物体的高度，通常使用“在同一时刻物高与影长的比例相等”的原理解决.


相似三角形的性质及应用 394500


应用举例及总结】


要点诠释：测量旗杆的高度的几种方法：























平面镜测量法 影子测量法 手臂测量法 标杆测量法


2.测量距离


测量不能直接到达的两点间的距离，常构造如下两种相似三角形求解。


1．如甲图所示，通常可先测量图中的线段DC、BD、CE的距离（长度），根据相似三角形的性质，求出AB的长.


2．如乙图所示，可先测AC、DC及DE的长，再根据相似三角形的性质计算AB的长.





要点诠释：


1．比例尺：表示图上距离比实地距离缩小的程度，比例尺= 图上距离/ 实际距离;


2．太阳离我们非常遥远，因此可以把太阳光近似看成平行光线．在同一时刻，两物体影子之比等于其对应高的比;


3．视点：观察事物的着眼点（一般指观察者眼睛的位置）;


4. 仰（俯）角：观察者向上（下）看时，视线与水平方向的夹角．





【典型例题】


类型一、相似三角形的性质


1. （2016•长春）如图，在▱ABCD中，点E在边BC上，点F在边AD的延长线上，且DF=BE，EF与CD交于点G．


（1）求证：BD∥EF；


（2）若=，BE=4，求EC的长．





【思路点拨】（1）根据平行四边的判定与性质，可得答案；


（2）根据相似三角形的判定与性质，可得答案．


【答案】B.


【解析】（1）证明：∵四边形ABCD是平行四边形，


∴AD∥BC．


∵DF=BE，


∴四边形BEFD是平行四边形，


∴BD∥EF；


（2）∵四边形BEFD是平行四边形，


∴DF=BE=4．


∵DF∥EC，


∴△DFG∽CEG，


∴=，


∴CE==4×=6．


【总结升华】本题考查了相似三角形的判定与性质，利用了平行四边形的判定与性质，相似三角形的判定与性质．


举一反三


【变式】在锐角△ABC中，AD,CE分别为BC,AB边上的高，△ABC和△BDE的面积分别等于18和2，DE=2,求AC边上的高.


【答案】过点B做BF⊥AC,垂足为点F，


∵AD,CE分别为BC,AB边上的高，


∴∠ADB=∠CEB=90°，


又∵∠B=∠B，


∴Rt△ADB∽Rt△CEB,


∴,


且∠B=∠B，


∴△EBD∽△CBA,


∴,


∴,


又∵DE=2，


∴AC=6，


∴





2.已知：如图，在△ABC与△CAD中，DA∥BC，CD与AB相交于E点，


且AE︰EB=1︰2，EF∥BC交AC于F点，△ADE的面积为1，求△BCE和△AEF的面积．





【答案与解析】∵DA∥BC，


∴△ADE∽△BCE．


∴S△ADE:S△BCE=AE2:BE2．


∵AE︰BE=1:2，


∴S△ADE:S△BCE=1:4．


∵S△ADE=1，


∴S△BCE=4．


∵S△ABC:S△BCE=AB:BE=3:2，


∴S△ABC=6．


∵EF∥BC，


∴△AEF∽△ABC．


∵AE:AB=1:3，


∴S△AEF:S△ABC=AE2:AB2=1:9．


∴S△AEF==．


【总结升华】注意，同底(或等底)三角形的面积比等于该底上的高的比；同高(或等高)三角形的面积比等于对应底边的比．当两个三角形相似时，它们的面积比等于对应线段比的平方，即相似比的平方．


举一反三：


相似三角形的性质及应用 394500


例题分析2】


【变式】如图，已知中，，，，，点在上， (与点不重合)，点在上.


(1)当的面积与四边形的面积相等时，求的长.


(2)当的周长与四边形的周长相等时，求的长.

















【答案】 (1)∵，








∽








.


(2)∵的周长与四边形的周长相等.





=6，





∽











.

















类型二、相似三角形的应用


3.（2015春•江津区校级月考）如图，直立在B处的标杆AB=2.4m，直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上（点F，B，D也在同一条直线上）．已知BD=8m，FB=2.5m，人高EF=1.5m，求树高CD．





【答案与解析】解：过E作EH⊥CD交CD于H点，交AB于点G，如下图所示：


由已知得，EF⊥FD，AB⊥FD，CD⊥FD，


∵EH⊥CD，EH⊥AB，


∴四边形EFDH为矩形，


∴EF=GB=DH=1.5米，EG=FB=2.5米，GH=BD=8米，


∴AG=AB﹣GB=2.4﹣1.5=0.9米，


∵EH⊥CD，EH⊥AB，


∴AG∥CH，


∴△AEG∽△CEH，


∴=，


∴=，


解得：CH=3.78米，


∴DC=CH+DH=3.78+1.5=5.28米．


答：故树高DC为5.2米．





【总结升华】本题考查了相似三角形在实际问题中的运用，关键是正确作出辅助线，构造出相似三角形．


举一反三：


【变式】已知：如图，阳光通过窗口照射到室内，在地面上留下1.5m宽的亮区DE.亮区一边到窗下的墙脚距离CE=1.2m，窗口高AB=1.8m，求窗口底边离地面的高度BC.





【答案】作EF⊥DC交AD于F.





∵AD∥BE，∴


又∵，


∴，


∴.


∵AB∥EF， AD∥BE，


∴四边形ABEF是平行四边形，


∴EF=AB=1.8m.


∴m.


4.（2015•齐齐哈尔）如图，正方形ABCB1中，AB=1．AB与直线l的夹角为30°，延长CB1交直线l于点A1，作正方形A1B1C1B2，延长C1B2交直线l于点A2，作正方形A2B2C2B3，延长C2B3交直线l于点A3，作正方形A3B3C3B4，…，依此规律，则A2014A2015= ．





【思路点拨】本题考查相似三角形的判定与性质以及正方形的性质，根据已知条件得到A1B1=，AA1=2，同理：A2A3=2（）2，A3A4=2（）3，从而找出规律答案即可求出．菁优


【答案与解析】2（）2014


解：∵四边形ABCB1是正方形，


∴AB=AB1，AB∥CB1，


∴AB∥A1C，


∴∠CA1A=30°，


∴A1B1=，AA1=2，


∴A1B2=A1B1=，


∴A1A2=2，


同理：A2A3=2（）2，


A3A4=2（）3，


…


∴AnAn+1=2（）n，


∴A2014A2015=2（）2014，


故答案为：2（）2014．


【总结升华】本题是相似性质的运用与找规律相结合的一道题，要注意从特殊到一般形式的变换规律.