初中数学苏科版八年级上册第三章 勾股定理3.1 勾股定理精品课件ppt

这是一份初中数学苏科版八年级上册第三章 勾股定理3.1 勾股定理精品课件ppt，共16页。PPT课件主要包含了1勾股定理，SA+SBSC，议一议，练一练等内容，欢迎下载使用。

八年级数学（上册）•苏科版
相传2500年前，毕达哥拉斯有一次在朋友家里做客时，发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系．
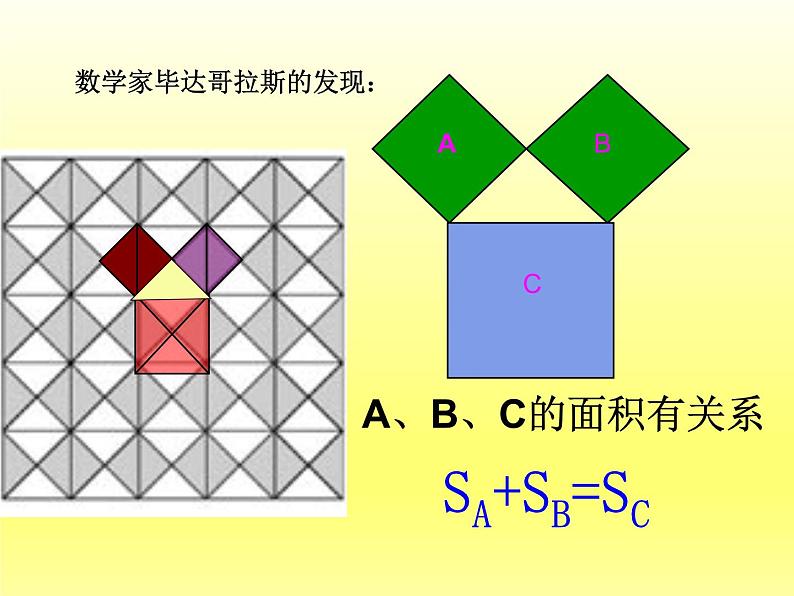
　　数学家毕达哥拉斯的发现：
A、B、C的面积有关系
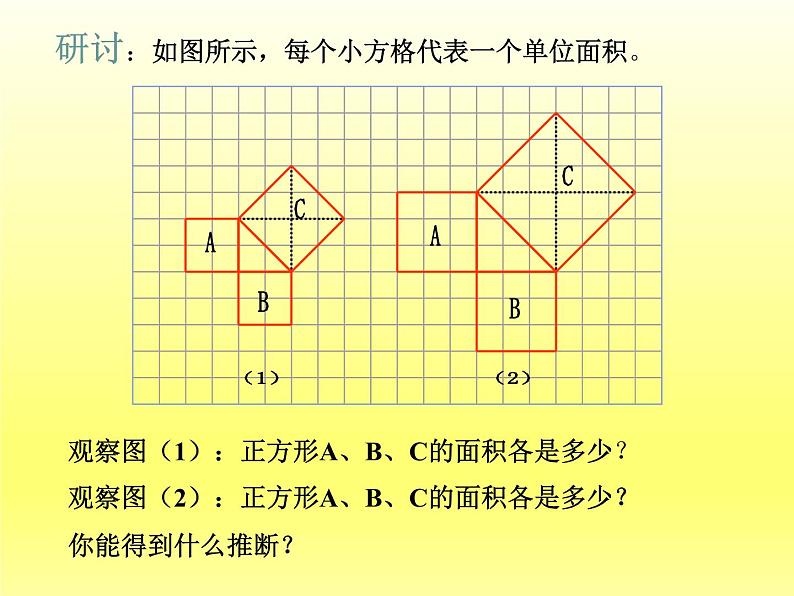
研讨：如图所示，每个小方格代表一个单位面积。
观察图（1）：正方形A、B、C的面积各是多少？
观察图（2）：正方形A、B、C的面积各是多少？
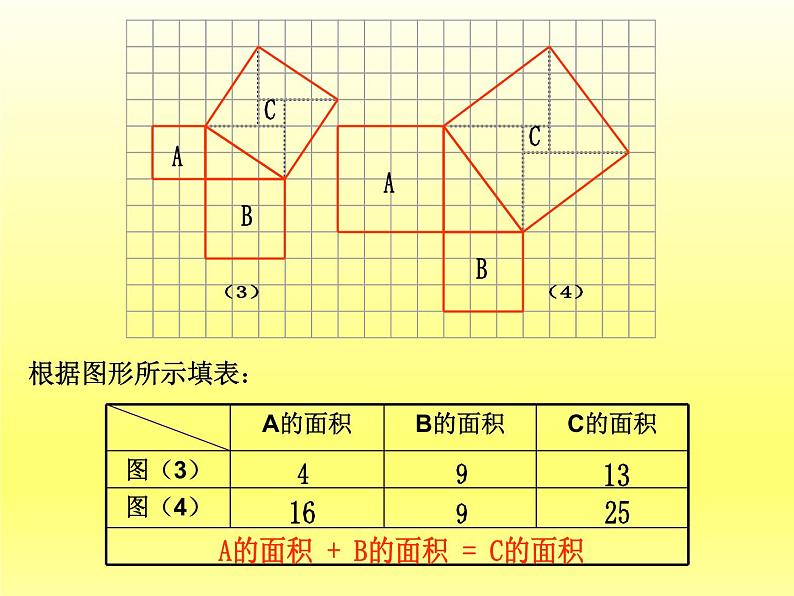
A的面积 + B的面积 = C的面积
正方形A的面积+正方形B的面积=正方形C的面积
（正方形的面积可以表示为边长的平方）
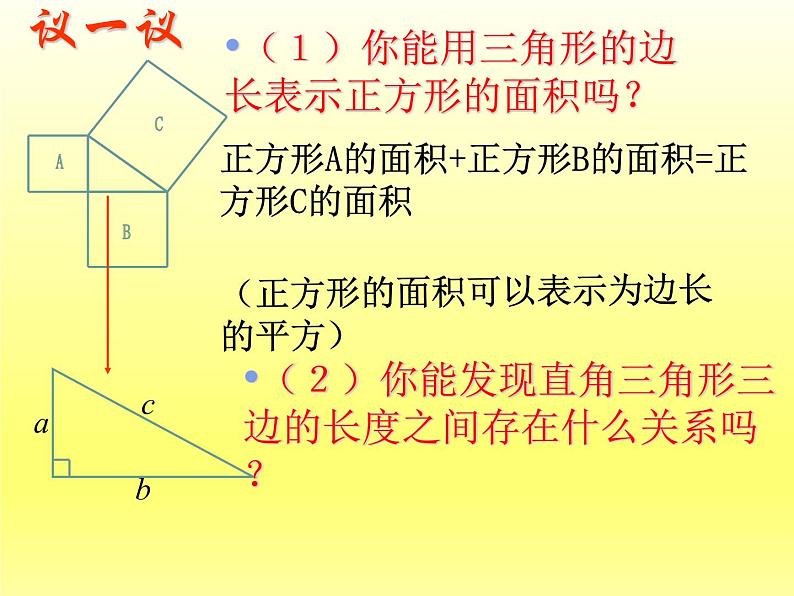
（１）你能用三角形的边长表示正方形的面积吗？
（２）你能发现直角三角形三边的长度之间存在什么关系吗？
如果直角三角形的两直角边分别为a，b ，斜边为c，那么
勾股定理（毕达哥拉斯定理）
例1、已知Rt△ABC中, ∠C=90°,BC= a ,AC= b ,AB=c已知a=6, b=8,求c;已知a =15 , c =17,求 b; 已知c = 13 ,b= 5,求a;(4)已知c=15 ,a:b=3:4,求 a,b.
1．求下列图中未知数x、y、z的值：
2．求下列直角三角形中未知边的长：
3.1　勾股定理（1）
3．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm,则正方形A，B，C，D的面积之和为___________cm2。
　　做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱，一根长为70厘米的木棒能否放入，为什么？试用今天学过的知识说明．
　　受台风格美影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？
已知, 折叠长方形的一边AD,使如图所示,折叠长方形的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,求EC的长