

湖北竹溪县丰溪中学2019—2020学年八年级数学期末学业水平检测试题(word版有答案)
展开2019—2020学年度第一学期期末学业水平检测
八年级数学试题
温馨提示:
1. 本试卷分第Ⅰ卷和第Ⅱ卷两部分,共8页。满分150分。考试用时120分钟。
2.答卷前,考生务必用0.5毫米黑色签字笔将自己的学校、班级、姓名填写在答题卡规定的位置上。
3.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。答案不能答在试题卷上。
4. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。
第Ⅰ卷(选择题,共36分)
一、选择题:本大题共12个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑.每小题涂对得3分,满分36分.
1.下列二次根式中,不能与合并的是
A.2 B. C. D.
2.因式分解,其中、、都为整数,则这样的的最大值是
A.1 B.4 C.11 D.12
3.下列运算正确的是
A. B.
C. D.
4.如果将分式(,均为正数)中字母的,的值分别扩大为原来的3倍,那么分式的值
A.扩大为原来的3倍 B.不变 C.缩小为原来的 D.扩大为原来的9倍
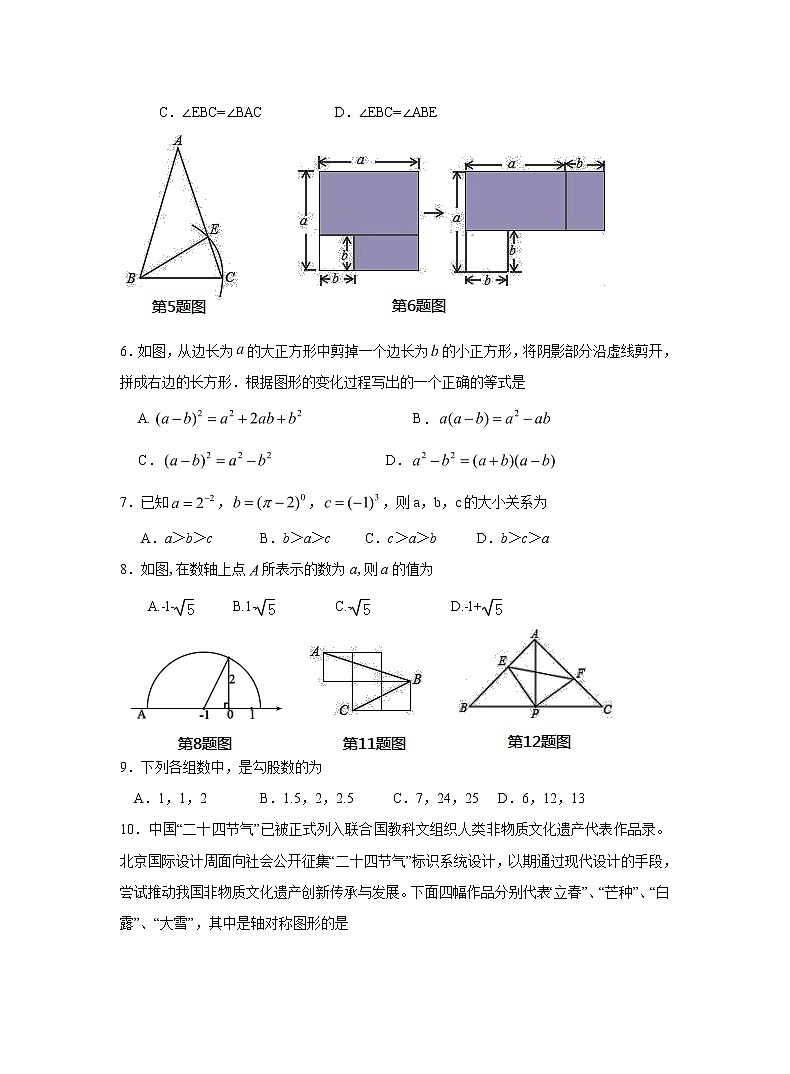
5.如图,已知等腰三角形,.若以点为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是
A.AE=EC B.AE=BE
C.∠EBC=∠BAC D.∠EBC=∠ABE
6.如图,从边长为的大正方形中剪掉一个边长为的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形.根据图形的变化过程写出的一个正确的等式是
A. B.
C. D.
7.已知,,,则a,b,c的大小关系为
A.a>b>c B.b>a>c C.c>a>b D.b>c>a
8.如图,在数轴上点所表示的数为a,则a的值为
A.﹣1﹣ B.1﹣ C.﹣ D.﹣1+
9.下列各组数中,是勾股数的为
A.1,1,2 B.1.5,2,2.5 C.7,24,25 D.6,12,13
10.中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录。北京国际设计周面向社会公开征集“二十四节气”标识系统设计,以期通过现代设计的手段,尝试推动我国非物质文化遗产创新传承与发展。下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是
11.如图是一个棱长为1的正方体的部分侧面展开图,点A,B,C是展开后小正方形的顶点,连接AB,BC,则∠ABC的大小是( )
A.60° B.50° C.45° D.30°
12.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE,PF分别交AB,AC于点E,F,给出下列四个结论:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四边形AEPF,上述结论正确的有
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷(非选择题,共114分)
二、填空题:本大题共8个小题,每小题5分,满分40分.
13.诺贝尔生理学或医学奖得主中国科学家屠呦呦,发现了一种长度约为0.000000456毫米的病毒,把0.000000456用科学记数法表示为 .
14.分解因式:3x2﹣12xy+12y2= .
15. 如图,在Rt△ABC中,∠B=90°,分别以点A,C为圆心,大于AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D,E,连接AE.当AB=3,BC=4时,则△ABE的周长为 .
16.若是一个完全平方式,那么= .
17.若二次根式与相等,则 , .
18. 关于的分式方程的解为正数,则的取值范围是
___________.
19.如图,,,如果射线上的点满足△OCE是等腰三角形,那么∠OEC的度数为 .
20.我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为,,,则该三角形的面积为S=.现已知△ABC的三边长分别为1,2,,则△ABC的面积为________.
三、解答题:本大题共7个小题,满分74分.解答时请写出必要的演推过程.
21.(本小题满分8分)
如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.
(1)求证:BD=CE;
(2)若AD=BD=DE,求∠BAC的度数.
22.(本小题满分8分)
如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
(1)请画出△ABC关于轴成轴对称的图形△,并写出、、 的坐标;
(2)在y轴上找一点,使的值最小,请画出点的位置.
23.(本小题满分10分)
如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”.
(1)下列分式:①;②;③;④.其中是“和谐分式”的是 (填写序号即可);
(2)若a为正整数,且为“和谐分式”,请写出a的值 ;
(3)在分式运算中,我们也会用到判断和谐分式时所需要的知识,请你用所学知识,化简
24.(本小题满分10分)
中国北京已获得2022年第24届冬季奥林匹克运动会举办权,北京也将创造历史,成为第一个既举办过夏奥会又举办冬奥会的城市。张家口也成为本届冬奥会的协办城市,为此,中国设计了第一条采用我国自主研发的北斗卫星导航系统的智能化高速铁路——京张高铁,作为2022年北京冬奥会重要交通保障设施。已知北京至张家口铁路,铁路全长约180千米.按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求高铁列车的平均行驶速度.
25.(本小题满分12分)
(1)如图1是一个重要公式的几何解释.请你写出这个公
式: ;
(2)如图2,已知,,且三点共线.
试证明;
(3)勾股定理是几何学中的明珠,千百年来,人们对它的证明趋之若骛,有资料表明,关于勾股定理的证明方法已有500余种。课本中介绍了比较有代表性的赵爽弦图。
伽菲尔德(Garfield,1881年任美国第20届总统)利用图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),请你写出该证明过程.
26.(本小题满分12分)
黑白双雄,纵横江湖;双剑合璧,天下无敌,这是武侠小说中的常见描述,其意思是指两个人合在一起,取长补短,威力无比,在二次根式中也常有这种相辅相成的“对子”,如:,,它们的积中不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解:
,.
像这样通过分子、分母同乘一个式子把分母中的根号化去的方法,叫做分母有理化。
解决问题:
(1)的有理化因式是 ;
将 分母有理化得 ;
.
27.(本小题满分14分)
通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形。如果我们新定义一种三角形——两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形。
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
(填“是”或不是);
(2)若某三角形的三边长分别为1、、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
(3)在中,两边长分别为,且,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
答案
一、选择题
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
C | C | B | B | C | D | B | A | C | D | C | C |
二、填空题
- ; 14. ; 15. 7; 16. ;
- 1 , 1; 18.; 19.; 20. 1 ;
三.解答题
- (1)过点A作AF⊥BC于F.……………1分
∵AB=AC,AD=AE.
∴BF=CF,DF=EF.……………………3分
∴BD=CE.……………………………4分
(2)∵AD=DE=AE
∴△ADE是等边三角形,∴∠DAE=∠ADE=60°.………5分
∵AD=BD,∴∠DAB=∠DBA.
∴∠DAB=∠ADE=30°.…………………………………6分
同理可求得∠EAC=30°,∴∠BAC=120°. ……………8分
22.解:(1)如图所示,△即为所求,
由图知,的坐标为(1,﹣1)、的坐标为(4,﹣2)、的坐标为(3,﹣4);
(2)如图所示,点即为所求.
评分标准:画出图形得2分,每写对一个坐标得1分;找对点位置得3分.
23.解:(1)②分式,不可约分,
∴分式是和谐分式,
故答案为:②; ……………2分
(2)∵分式为和谐分式,且a为整数,
∴ (每写对一个数值得1分) ……………5分
(3)
……………10分
24.
……………3分
……………7分
………9分
答:高铁列车的平均行驶速度为270千米/时. ……………10分
25.⑴ 这个公式为. ……………2分
⑵ ∵,∴.
.
由于点共线,
所以. ……………6分
⑶ 梯形的面积为
;
另一方面,梯形可分成三个直角三角形,其面积又可以表示成
∴,即 ……………12分
- (1); ; (每空2分)……………4分
(3)
又
……………12分
- (1)是; ……………2分
(2)
该三角形一定是奇异三角形. ……………4分
(3) ,
;
,
,
,
. ……………8分
拓展:,
,
,
,
,
,
. …………14分








