初中数学人教版七年级上册第三章 一元一次方程综合与测试精品同步练习题

这是一份初中数学人教版七年级上册第三章 一元一次方程综合与测试精品同步练习题，共8页。试卷主要包含了列方程解应用题等内容，欢迎下载使用。

追击与相遇类专项练（一）





1．A，B两地相距340千米，已知甲车的速度为60千米/小时，乙车的速度为80千米/小时．


（1）如果甲车从A地向B地先开出1小时后，乙车从B地出发，两车相向而行，乙车出发多少小时后两车相遇？


（2）如果（1）中两车相遇半小时后，乙车返回追赶甲车，能否在甲车到达B地前追上？











2．家住山脚下的孔明同学想从家出发登山游玩，据以往的经验，他获得如下信息：


（1）他下山时的速度比上山时的速度每小时快1千米；


（2）他上山2小时到达的位置，离山顶还有1千米；


（3）抄近路下山，下山路程比上山路程近2千米；


（4）下山用1个小时；


根据上面信息，他作出如下计划：


（1）在山顶游览1个小时；


（2）中午12：00回到家吃中餐．


若依据以上信息和计划登山游玩，请问：孔明同学应该在什么时间从家出发？














3．甲乙两人骑自行车，同时从相距65千米的AB两地相向而行，甲速度为17.5千米一小时，乙速度15千米一小时，几小时后，甲乙两人相距32.5千米？











4．列方程解应用题：


A、B两城相距720千米，普快列车从A城出发120千米后，特快列车从B城开往A城，6小时后两车相遇，若普快列车的速度是特快列车速度的，求两车的速度．














5．甲、乙两站路程为360km，一列慢车从甲站开出，每小时行48km，一列快车从乙站开出，每小时行72km．


（1）两车同时开出，相向而行，多少小时相遇？


（2）若慢车先开出20分钟，快车再出发，两车同向而行，快车多少时间追上慢车？

















6．一架飞机在两城之间飞行，风速为24千米/小时，顺风飞行需2小时，逆风飞行需要3小时．


（1）求无风时飞机的飞行速度；


（2）求两城之间的距离．

















7．甲、乙两汽车站相距190km，一辆汽车以30km/h的速度从甲地开往乙地，出发2h后，一辆摩托车以50km/h的速度也从甲地开往乙地，摩托车需要多长时间才能追上汽车？








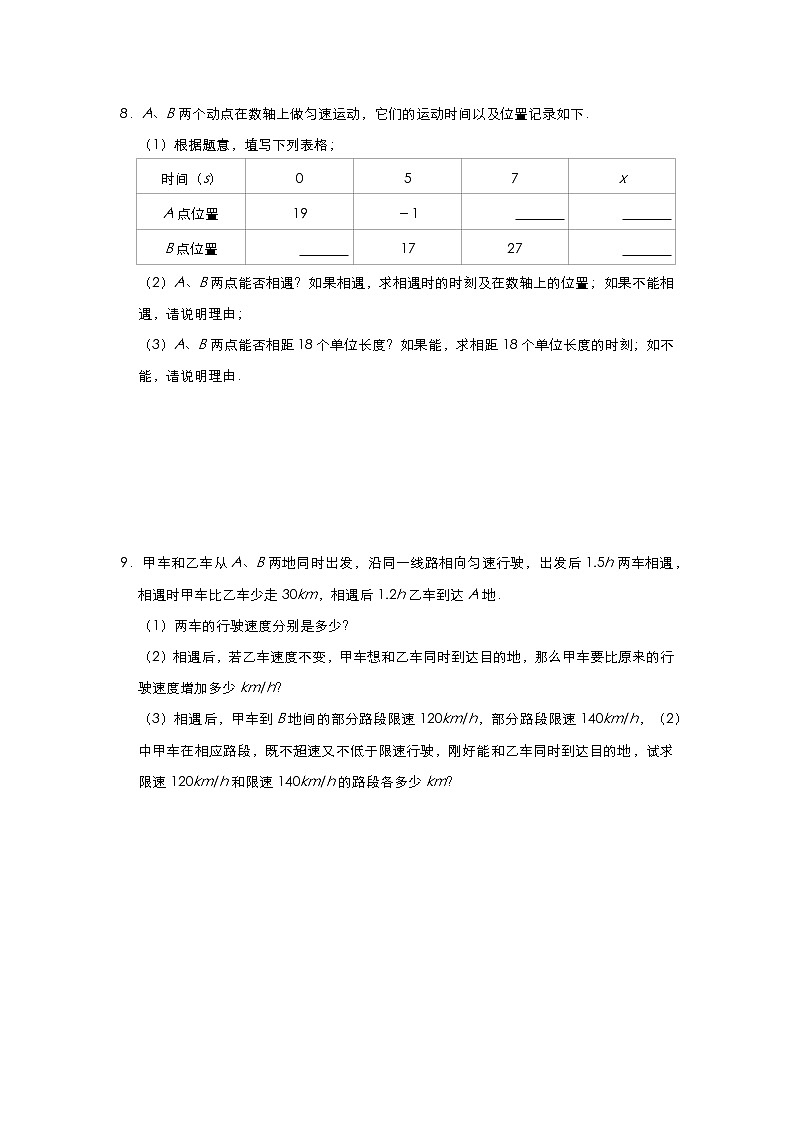
8．A、B两个动点在数轴上做匀速运动，它们的运动时间以及位置记录如下．


（1）根据题意，填写下列表格；


（2）A、B两点能否相遇？如果相遇，求相遇时的时刻及在数轴上的位置；如果不能相遇，请说明理由；


（3）A、B两点能否相距18个单位长度？如果能，求相距18个单位长度的时刻；如不能，请说明理由．

















9．甲车和乙车从A、B两地同时出发，沿同一线路相向匀速行驶，出发后1.5h两车相遇，相遇时甲车比乙车少走30km，相遇后1.2h乙车到达A地．


（1）两车的行驶速度分别是多少？


（2）相遇后，若乙车速度不变，甲车想和乙车同时到达目的地，那么甲车要比原来的行驶速度增加多少km/h？


（3）相遇后，甲车到B地间的部分路段限速120km/h，部分路段限速140km/h，（2）中甲车在相应路段，既不超速又不低于限速行驶，刚好能和乙车同时到达目的地，试求限速120km/h和限速140km/h的路段各多少km？























10．某校综合实践小分队成一列在野外拓展训练，在队伍中的队长数了一下他前后的人数，发现他前面人数是他后面的三倍，他往前超了5位队友后，发现他前面的人数和他后面的人数一样多．问：


（1）这列队伍一共有多少名学生？


（2）这列队伍要过一座240米的大桥，为拓展训练和安全需要，相邻两个学生保持相同的间距，队伍行进速度为3米/秒，从第一位学生刚上桥到全体通过大桥用了90秒时间，请问相邻两个学生间距离为多少米（不考虑学生身材的大小）？





















































参考答案


1．解：（1）乙车出发x小时后两车相遇，


根据题意得：（60+80）x+60＝340


解得：x＝2，


答：乙车出发2小时后两车相遇；


（2）乙车追上甲车需y小时，


根据题意得：（80﹣60）y＝0.5（80+60），


解得：y＝3.5，


而甲车还需﹣3.5＝小时到达B地，


答：两车相遇半小时后，乙车返回追赶甲车，不能在甲车到达B地前追上．


2．解：设上山的速度为v，下山的速度为（v+1），则


2v+1＝v+1+2，


解得 v＝2．


即上山速度是2千米/小时．


则下山的速度是3千米/小时，山高为5千米．


则计划上山的时间为：5÷2＝2.5（小时），


计划下山的时间为：1小时，


则共用时间为：2.5+1+1＝4.5（小时），


所以出发时间为：12：00﹣4小时30分钟＝7：30．


答：孔明同学应该在7点30分从家出发．


3．解：设经过x小时，甲、乙两人相距32.5千米．有两种情况：


①两人没有相遇相距32.5千米，那么两人共同走了（65﹣32.5）千米，


根据题意可以列出方程x（17.5+15）＝65﹣32.5，


解得x＝1；


②两人相遇后相距32.5千米，那么两人共同走了（65+32.5）千米，


根据题意可以列出方程x（17.5+15）＝65+32.5，


解得x＝3．


答：经过1或3小时，甲、乙两人相距32.5千米．


4．解：设特快列车速度为x千米/时，则普快列车的速度为x千米/时，由题意，得


120+6（x+x）＝720，


解得：x＝60，


∴普快列车的速度为×60＝40千米/时．


答：特快列车速度为60千米/时，则普快列车的速度为40千米/时．


5．解：（1）设两车同时开出相向而行，经x小时相遇，即


72x+48x＝360，


解得：x＝3．


答：经过3小时两车相遇．





（2）设快车行驶y小时追上慢车；根据题意有：


48（y+）+360＝72y，


解得：y＝．


答：快车小时追上慢车．


6．解：（1）设无风时飞机的飞行速度为x千米/小时，由题意得


2（x+24）＝3（x﹣24）


解得：x＝120


答：无风时飞机的飞行速度是120千米/时；


（2）2（x+24）＝288千米


答：两城之间的距离是288千米．


7．解：设摩托车需要x小时长时间才能追上汽车，依题意有


（50﹣30）x＝30×2，


解得x＝3．


故摩托车需要3小时长时间才能追上汽车．


8．解：（1）填表如下：


（2）根据题意可得：﹣4x+19＝5x﹣8


解得：x＝3．


答：相遇的时刻为3秒，在数轴上的位置为7；


（3）根据题意可得：﹣4x+19﹣（5x﹣8）＝18


解得：x＝1；


根据题意可得：5x﹣8﹣（﹣4x+19）＝18


解得：x＝5．


综上所述，x＝1或5时，A、B两点能否相距18个单位长度．


9．（1）解：设乙车速度为vkm/h，依题意有


1.2v＝1.5v﹣30，


解得：v＝100，


则甲车的速度为：，


即．


答：乙的速度为：100km/h，甲的速度为：80km/h；





（2）设甲车的行驶速度比原来增加akm/h，则有：


（80+a）×1.2＝100×1.5，


解得：a＝45．


答：甲车要比原来的行驶速度增加45km/h；





（3）设限速120km/h的路段长xkm，则限速140km/h的路段长（150﹣x）km，


则依题意有，


解得：x＝108，150﹣x＝42．


答：限速120km/h路段长108km，限速140km/h的路段42km．


10．解：（1）设开始队长后面有x名学生，由题意得


x+5＝3x﹣5，


解得x＝5，


共有学生4x+1＝21（名）


答：这列队伍一共有21名学生；





（2）设相邻两个学生间距离为y米，由题意得


20y+240＝3×90，


解得 y＝1.5


答：相邻两个学生间距离为1.5米．


时间（s）
0
5
7
x
A点位置
19
﹣1


B点位置

17
27

时间（s）
0
5
7
x
A点位置
19
﹣1
﹣9
﹣4x+19
B点位置
﹣8
17
27
5x﹣8