初中数学人教版九年级上册第二十四章 圆综合与测试精品测试题

这是一份初中数学人教版九年级上册第二十四章 圆综合与测试精品测试题，共18页。试卷主要包含了50，5°，等内容，欢迎下载使用。

难度系数：0.50


一．选择题


1．如图，点A，B，C都在⊙O上，∠A＝∠B＝20°，则∠AOB等于（ ）





A．40°B．60°C．80°D．100°


2．下列说法中，不正确的个数是（ ）


①直径是弦；②经过圆内一定点可以作无数条直径；③平分弦的直径垂直于弦；④过三点可以作一个圆；⑤过圆心且垂直于切线的直线必过切点．


A．1个B．2个C．3个D．4个


3．⊙O的半径为3，锐角三角形ABC内接于⊙O，且BC＝3．则∠A的度数为（ ）


A．30°B．150°C．30°或150°D．不能确定


4．若圆锥的底面半径为2，母线长为5，则圆锥的侧面积为（ ）


A．5πB．10π C．20π D．40π


5．如图，AD是半圆的直径，点C是弧BD的中点，∠ADC＝55°，则∠BAD等于（ ）





A．50°B．55°C．65°D．70°


6．如图，⊙O的直径AB＝6，若∠BAC＝50°，则劣弧AC的长为（ ）





A．2πB．C．D．


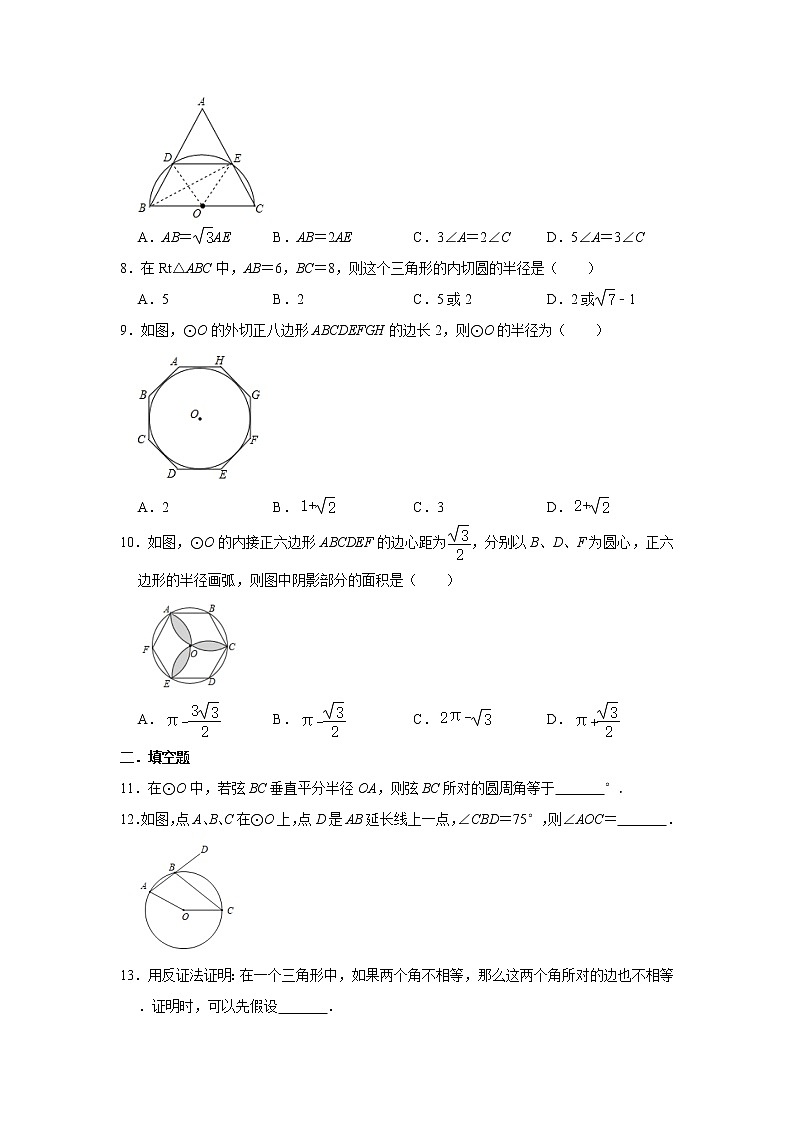
7．如图，在△ABC中，以边BC为直径做半圆，交AB于点D，交AC于点E，连接DE，若＝2＝2，则下列说法正确的是（ ）





A．AB＝AEB．AB＝2AEC．3∠A＝2∠CD．5∠A＝3∠C


8．在Rt△ABC中，AB＝6，BC＝8，则这个三角形的内切圆的半径是（ ）


A．5B．2C．5或2D．2或﹣1


9．如图，⊙O的外切正八边形ABCDEFGH的边长2，则⊙O的半径为（ ）





A．2B．C．3D．


10．如图，⊙O的内接正六边形ABCDEF的边心距为，分别以B、D、F为圆心，正六边形的半径画弧，则图中阴影部分的面积是（ ）





A．B．C．D．


二．填空题


11．在⊙O中，若弦BC垂直平分半径OA，则弦BC所对的圆周角等于 °．


12．如图，点A、B、C在⊙O上，点D是AB延长线上一点，∠CBD＝75°，则∠AOC＝ ．





13．用反证法证明：在一个三角形中，如果两个角不相等，那么这两个角所对的边也不相等．证明时，可以先假设 ．


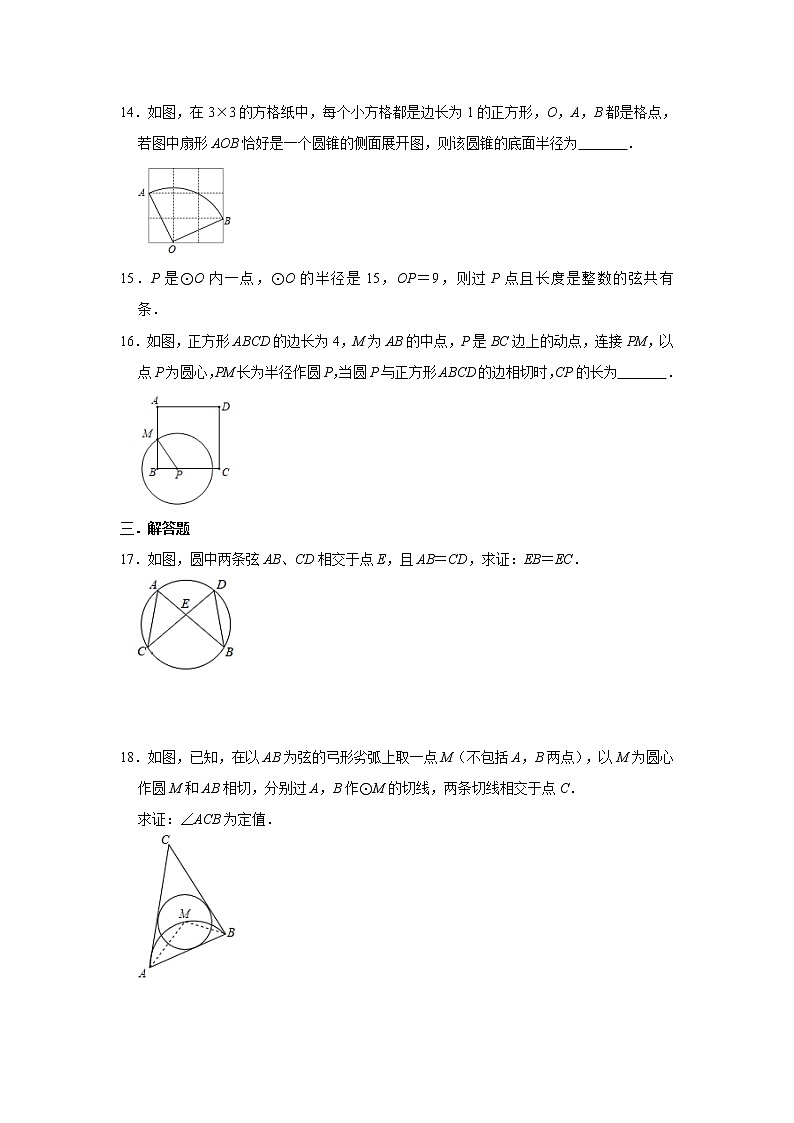
14．如图，在3×3的方格纸中，每个小方格都是边长为1的正方形，O，A，B都是格点，若图中扇形AOB恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为 ．





15．P是⊙O内一点，⊙O的半径是15，OP＝9，则过P点且长度是整数的弦共有 条．


16．如图，正方形ABCD的边长为4，M为AB的中点，P是BC边上的动点，连接PM，以点P为圆心，PM长为半径作圆P，当圆P与正方形ABCD的边相切时，CP的长为 ．





三．解答题


17．如图，圆中两条弦AB、CD相交于点E，且AB＝CD，求证：EB＝EC．











18．如图，已知，在以AB为弦的弓形劣弧上取一点M（不包括A，B两点），以M为圆心作圆M和AB相切，分别过A，B作⊙M的切线，两条切线相交于点C．


求证：∠ACB为定值．








19．如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O点D．点E在⊙O上．


（1）若∠AOC＝40°，求∠DEB的度数；


（2）若OC＝3，OA＝5，求AB的长．











20．如图，在△ABC中，AB＝AC＝2，BC＝4，⊙O是△ABC的外接圆．


（1）求⊙O的半径；


（2）若在同一平面内的⊙P也经过B、C两点，且PA＝2，请直接写出⊙P的半径的长．














21．如图所示，AB是圆O直径，OD⊥弦BC于点F，且交⊙O于点E，若∠AEC＝∠ODB．


（1）判断直线BD和圆O的位置关系，并给出证明；


（2）当CE＝5，BC＝8时，求圆O的半径．

















22．如图，已知四边形ABCD内接于圆O，连结BD，∠BAD＝105°，∠DBC＝75°


（1）求证：BD＝CD；


（2）若圆O的半径为3，求的长．








23．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．


（1）判断直线DE与⊙O的位置关系，并说明理由；


（2）如果AB＝5，BC＝6，求DE的长．








24．如图，⊙O为△ABC的外接圆，D为OC与AB的交点，E为线段OC延长线上一点，且∠EAC＝∠ABC．


（1）求证：直线AE是⊙O的切线．


（2）若D为AB的中点，CD＝6，AB＝16


①求⊙O的半径；


②求△ABC的内心到点O的距离．





参考答案


一．选择题


1．解：连接OC．


∵OB＝OC，


∴∠B＝∠BCO，


同理，∠A＝∠ACO


∴∠ACB＝∠A+∠B＝40°，


∴∠AOB＝2∠ACB＝80°．


故选：C．





2．解：①直径是特殊的弦．所以①正确，不符合题意；


②经过圆心可以作无数条直径．所以②不正确，符合题意；


③平分弦（不是直径）的直径垂直于弦．所以③不正确，符合题意；


④过不在同一条直线上的三点可以作一个圆．所以④不正确，符合题意；


⑤过圆心且垂直于切线的直线必过切点．所以⑤正确，不符合题意．


故选：C．


3．解：如图，锐角三角形ABC内接于⊙O，





∵⊙O的半径为3，BC＝3．


∴OB＝OC＝BC＝3，


∴△OBC是等边三角形，


∴∠BOC＝60°，


∴∠A＝BOC＝30°，


∴∠A的度数为30°，


故选：A．


4．解：圆锥的侧面积为：π×2×5＝10π．


故选：B．


5．解：连接OB，OC


∵∠ADC＝55°，


∴∠AOC＝2∠ADC＝110°，


∴弧AC＝110°，


∵AD是半圆的直径，


∴∠COD＝70°，


∵C是弧BD的中点，


∴∠BOD＝2∠COD＝140°，


∴∠BAD＝∠BOD＝70°，


故选：D．





6．解：如图，连接CO，


∵∠BAC＝50°，AO＝CO＝3，


∴∠ACO＝50°，


∴∠AOC＝80°，


∴劣弧AC的长为＝，


故选：D．





7．解：∵＝2＝2，


∴∠BOD＝∠EOC＝∠DOE，


∵∠BOD+∠EOC+∠DOE＝180°，


∴∠BOD＝∠EOC＝45°，∠DOE＝90°，


∵OB＝OD，


∴∠OBD＝∠ODB＝67.5°，


同理，∠OEC＝∠OCE＝67.5°，


∴∠A＝45°，


∵BC为直径，


∴∠AEB＝∠CEB＝90°，


∴AB＝AE，故A、B错误；


3∠A＝135°，2∠C＝135°，


∴3∠A＝2∠C，C正确；


5∠A＝225°，3∠C＝202.5°，


∴5∠A≠3∠C，D错误；


故选：C．


8．解：设直角三角形ABC内切圆的圆心为点I，半径为r，


三边上的切点分别为D、E、F，


连接ID、IE、IF，


得正方形，则正方形的边长即为r，


如图所示：





当BC为直角边时，


AC＝＝10，


根据切线长定理，得


AD＝AF＝AB﹣BD＝6﹣r，


CE＝CF＝BC﹣BE＝8﹣r，


∴AF+FC＝AC＝10，


即6﹣r+8﹣r＝10，解得r＝2；


当BC为斜边时，


AC＝＝2，


根据切线长定理，得


BD＝BF＝6﹣r，


CE＝CF＝2﹣r，


∴BC＝BF+CF＝6﹣r+2﹣r＝8，


解得r＝﹣1．


答：这个三角形的内切圆的半径是2或﹣1．


故选：D．


9．解：设DE与⊙O相切于点N，连接OD、OE、ON，作DM⊥OE于M，如图所示：


则ON⊥DE，DE＝2，OD＝OE，∠DOE＝＝45°，


∵DM⊥OE，


∴△ODM是等腰直角三角形，


∴DM＝OM，OE＝OD＝DM，


设OM＝DM＝x，则OD＝OE＝x，EM＝OE﹣OM＝（﹣1）x，


在Rt△DEM中，由勾股定理得：x2+（﹣1）2x2＝22，


解得：x2＝2+，


∵△ODE的面积＝DE×ON＝OE×DM，


∴ON＝＝＝＝+1，


即⊙O的半径为：1+；


故选：B．





10．解：如图，连接OB，OA，作OM⊥AB于点M，则OM＝．


∵∠AOB＝＝60°，AO＝OB，


∴BO＝AB＝AO，AM＝AB＝AO，OM＝，


∴，


∴AO＝1，


∴BO＝AB＝AO＝1，


∴S△AOB＝AB×OM＝×1×＝，


∵S扇形AOB＝＝，


∴阴影部分面积是：（﹣）×6＝π﹣．


故选：A．





二．填空题


11．解：如图，





∵弦BC垂直平分半径OA，


∴OD：OB＝1：2，


∴∠BOD＝60°，


∴∠BOC＝120°，


∴弦BC所对的圆周角等于60°或120°．


故答案为：60°或120°．


12．解：在优弧AC上取点E，连接AE，CE，





∵∠ABC＝180°﹣∠E，∠ABC＝180°﹣∠CBD，∠CBD＝75°，


∴∠E＝∠CBD＝75°．


∴∠AOC＝2∠E＝150°，


故答案为：150°．





13．解：反证法证明：在一个三角形中，如果两个角不相等，那么这两个角所对的边也不相等．


证明时，可以先假设这两个角所对的边相等，


故答案为：这两个角所对的边相等．


14．解：∵每个小方格都是边长为1的正方形，


∴AO＝＝，


∵∠AOB＝90°，


∴＝2πr，


∴r＝．


故答案是：．


15．解：如图示，


作AB⊥OP于P，


AP＝BP，


在Rt△AOP中，OP＝9，OA＝15，


AP＝＝12，


∴AB＝24，


故过点P的弦的长度在24和30之间，根据圆的对称性可得，二者之间的每个整数值的弦各2条，共10条，


所以过点P的弦中长度为整数的弦的条数为10+2＝12条．


故答案为12．





16．解：如图1中，当⊙P与直线CD相切时，设PC＝PM＝x．





在Rt△PBM中，∵PM2＝BM2+PB2，


∴x2＝22+（4﹣x）2，


∴x＝2.5，


∴CP＝2.5；


如图2中当⊙P与直线AD相切时．设切点为K，连接PK，则PK⊥AD，四边形PKDC是矩形．





∴PM＝PK＝CD＝2BM，


∴BM＝2，PM＝4，


在Rt△PBM中，PB＝＝2，


∴CP＝BC﹣PB＝4﹣2．


综上所述，CP的长为2.5或4﹣2．


故答案是：2.5或4﹣2．


三．解答题


17．证明：如图，连接AD，


∵AB＝CD，


∴＝，


∴﹣＝﹣，即＝，


∴∠BAD＝∠CDA，


∴AE＝DE，


又∵AB＝CD，


∴AE＝CE．





18．证明：连接AM，BM，


由题意得：M是内心，


∴AM平分∠CAB，BM平分∠ABC，


∴∠CAM＝∠BAM，∠CBM＝∠ABM，


∴∠AMB＝180°﹣∠BAM﹣∠ABM，


∴∠BAM+∠ABM＝180°﹣∠AMB，


△ABC中，∠C＝180°﹣（∠CAB+∠ACB）＝180°﹣2∠BAM﹣2∠ABM＝180°﹣2（180°﹣∠AMB）＝2∠AMB﹣180°，


∵所在圆是个定圆，弦AB和半径都是定值，


∴∠AMB为定值，


∴∠ACB为定值2∠AMB﹣180°．


19．解：（1）∵AB是⊙O的一条弦，OD⊥AB，


∴弧AD＝弧BD，


∴∠DEB＝∠AOC＝×40°＝20°；


（2）∵AB是⊙O的一条弦，OD⊥AB，


∴AC＝BC，即AB＝2AC，


在Rt△AOC中，AC＝＝＝4，


则AB＝2AC＝8．


20．解：（1）过点A作AD⊥BC，垂足为D，连接OB、OC，


∵AB＝AC，AD⊥BC，


∴AD垂直平分BC，


∵OB＝OC，


∴点O在BC的垂直平分线上，即O在AD上，


∵BC＝4，


∴BD＝BC＝2，


∵在Rt△ABD中，∠ADB＝90°，AB＝2，


∴AD＝＝6，


设OA＝OB＝r，则OD＝6﹣r．


∵在Rt△OBD中，∠ODB＝90°，


∴OD2+BD2＝OB2，即（6﹣r）2+22＝r2．


解得r＝，


即⊙O的半径为，


（2）当⊙P也经过B、C两点，


则设PB＝r，


PA＝2，则PD＝6﹣2＝4或6+2＝8，


BD＝2，


∴PB＝＝2


或PB＝＝2．


所以⊙P的半径的长为2或2．





21．解：（1）直线BD和⊙O相切．


证明：∵∠AEC＝∠ODB，∠AEC＝∠ABC，


∴∠ABC＝∠ODB，


∵OD⊥BC，


∴∠DBC+∠ODB＝90°，


∴∠DBC+∠ABC＝90°，


∴∠DBO＝90°，


∴直线BD和⊙O相切；


（2）∵OD⊥BC，BC＝8，


∴BF＝CF＝4，


在Rt△CEF中，EF＝＝3，


设圆O的半径为r，则OF＝r﹣3，


在Rt△OBF中，OB2＝OF2+BF2，即r2＝（r﹣3）2+42，


解得，r＝，即圆O的半径为．


22．（1）证明：∵四边形ABCD内接于圆O，


∴∠C＝180°﹣∠BAD＝75°，


∵∠DBC＝75°，


∴∠DBC＝∠C，


∴DB＝DC；


（2）解：连接OB、OC，


∵∠DBC＝∠C＝75°，


∴∠BDC＝30°，


由圆周角定理得，∠BOC＝2∠BDC＝60°，


∴的长＝＝π．





23．解：（1）相切，理由如下：


连接AD，OD，


∵AB为⊙O的直径，


∴∠ADB＝90°．


∴AD⊥BC．


∵AB＝AC，


∴CD＝BD＝BC．


∵OA＝OB，


∴OD∥AC．


∴∠ODE＝∠CED．


∵DE⊥AC，


∴∠ODE＝∠CED＝90°．


∴OD⊥DE．


∴DE与⊙O相切．





（2）由（1）知∠ADC＝90°，


∴在Rt△ADC中，由勾股定理 得


AD＝＝4．


∵SACD＝AD•CD＝AC•DE，


∴×4×3＝×5DE．


∴DE＝．


24．解：（1）证明：连接AO，并延长AO交⊙O于点F，连接CF





∵AF是直径


∴∠ACF＝90°


∴∠F+∠FAC＝90°，


∵∠F＝∠ABC，∠ABC＝∠EAC


∴∠EAC＝∠F


∴∠EAC+∠FAC＝90°


∴∠EAF＝90°，且AO是半径


∴直线AE是⊙O的切线．


（2）①如图，连接AO，





∵D为AB的中点，OD过圆心，


∴OD⊥AB，AD＝BD＝AB＝8，


∵AO2＝AD2+DO2，


∴AO2＝82+（AO﹣6）2，


∴AO＝，


∴⊙O的半径为；


②如图，作∠CAB的平分线交CD于点H，连接BH，过点H作HM⊥AC，HN⊥BC，





∵OD⊥AB，AD＝BD


∴AC＝BC，且AD＝BD


∴CD平分∠ACB，且AH平分∠CAB


∴点H是△ABC的内心，且HM⊥AC，HN⊥BC，HD⊥AB


∴MH＝NH＝DH


在Rt△ACD中，AC＝＝＝BC，


∵S△ABC＝S△ACH+S△ABH+S△BCH，


∴×16×6＝×10×MH+×16×DH+×10×NH，


∴DH＝，


∵OH＝CO﹣CH＝CO﹣（CD﹣DH），


∴OH＝﹣（6﹣）═5．