数学七年级下册6.2 立方根图文课件ppt

这是一份数学七年级下册6.2 立方根图文课件ppt，共23页。PPT课件主要包含了算一算，填一填，作业设计，或±1，一双基练习，二创新提升，三探究拓展等内容，欢迎下载使用。

劳动节即将来临,学生们纷纷向他们敬爱的老师表达心意,刘老师所任教的两个班的课代表一同前往老师办公室,他们手中捧着两个形状、大小一模一样的礼盒,并对老师说:“我代表我班的同学向老师敬礼,并以此小礼物代表我们对老师的敬意.”说完,两个课代表相视一笑,请老师猜一猜里面装的东西是否一样,里面物体的体积是否一样.老师知道,他们葫芦里肯定又要卖什么药,就郑重其事地说出两个盒子的大小虽然一样,但里面所装的物体的形状肯定不一样.虽然它们的体积相同,但一定有其他不同的地方.
一、创设情境,导入新课
刘老师打开纸盒一看，发现里面装的果然是两个不同形状的水晶一样的透明饰物，一个是圆球形的,一个是正方体形的,并且盒子里面各有一张纸条,内容为“经过测算,其体积为125 cm3”.
同学们,你们知道这两个饰物除了形状不同以外还有什么不同吗?
你能求出球的半径和正方体的棱长吗?
球的半径与正方体的棱长
二、师生互动,课堂探究
(一)提出问题,引发讨论
我们发现,求立方运算时,当底数互为相反数时,其立方值也是一对互为相反数的数,这与平方运算不同,平方运算的底数互为相反数时,其平方值相等,故一个正数的平方根有两个值,但一个正数的立方根却只有一个值,什么是立方根呢?
负数有立方根,并且其立方根仍为负数.
类似平方根的定义可知,若x3=a,则x为a的立方根,记为a,读作三次根号a.负数没有平方根,负数有无立方根呢?
2.开平方与平方互为逆运算,同样开立方与立方也互为逆运算.
8的立方根为 ,记为 ；-8的立方根为 ,记为 .
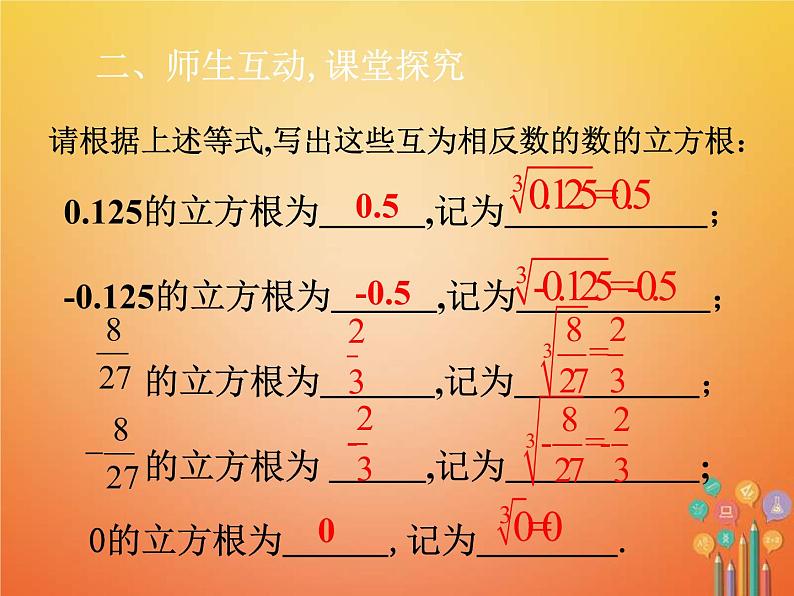
请根据上述等式,写出这些互为相反数的数的立方根：
0.125的立方根为 ,记为 ；-0.125的立方根为 ,记为 ；
0的立方根为 ,记为 .
上述过程都是求一个数的立方根的运算,把求一个数的立方根的运算,叫做开立方.开立方与立方运算互为逆运算.
故正方体的体积为125时,其边长为 ,
(二)导入知识,解释疑难
既然正数的立方是正数,负数的立方是负数,那么正数的立方根为正数,负数的立方根为负数,同理0的立方根是0.
因为 = ； = ；所以 ; 因为 = ； = ；所以 .
练习： (1)求下列各数的立方根： ①0； ②8 ；③-125.
(1)若正方体的棱长为1,则其体积为1；若正方体的棱长为2,则其体积为8；若正方体的棱长为4,则其体积为64；若其棱长为8,则其体积为512, …,当棱长为2n时,其体积为多少?
解:正方体棱长为1,则体积为1,棱长为2,则体积为8,比较两者棱长扩大到原来的2倍,体积扩大到原来的8倍,故当棱长为2n时,体积为8n3.
(三)归纳总结,知识回顾
这节课学习了立方根的概念,立方根的表示方法以及如何求一个数的立方根.用计算器求任意数的立方根时,可先求出该数的绝对值的立方根,再根据该数的正负决定其值,注意区分平方根与立方根.
(一)双基练习1.某数的立方根等于它本身,这个数是多少？
3.某金属冶炼厂将27个大小相同的立方体钢铁在炉火中熔化后浇铸成一个长方体钢铁,此长方体的长、宽、高分别为160 cm、80 cm和40 cm,求原立方体钢铁的棱长.