北师大版2020年九年级数学上册 第二次月考模拟试卷三（含答案）

北师大版2020年九年级数学上册

第二次月考模拟试卷

一、选择题

1．若点A（1，a）在反比例函数y=﹣的图象上，则a为（　　）

A．﹣2 B．2 C． D．﹣

2．若△ABC∽△DEF，相似比为1：3，则△ABC与△DEF的面积比为（　　）

A．1：9 B．1：3 C．1：2 D．1：

3．如图所示的是一个封闭的几何体，则题俯视图可能是（　　）

  A． B． C． D．

4．关于x的方程x2﹣mx﹣1=0根的情况是（　　）

A．有两个不相等的实数根     B．有两个相等的实数根

C．没有实数根             D．不能确定的

5．如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数的图象上，点D的坐标为（4，3），则k的值为（　　）

A．20 B．32 C．24 D．27

6．为了有效保护环境，某居委会倡议居民将生活垃圾进行可回收的、不可回收的和有害的分类投放，一天，小林把垃圾分装在三个袋中，则他任意投放垃圾，把三个袋子都放错位的概率是（　　）

A． B． C． D．

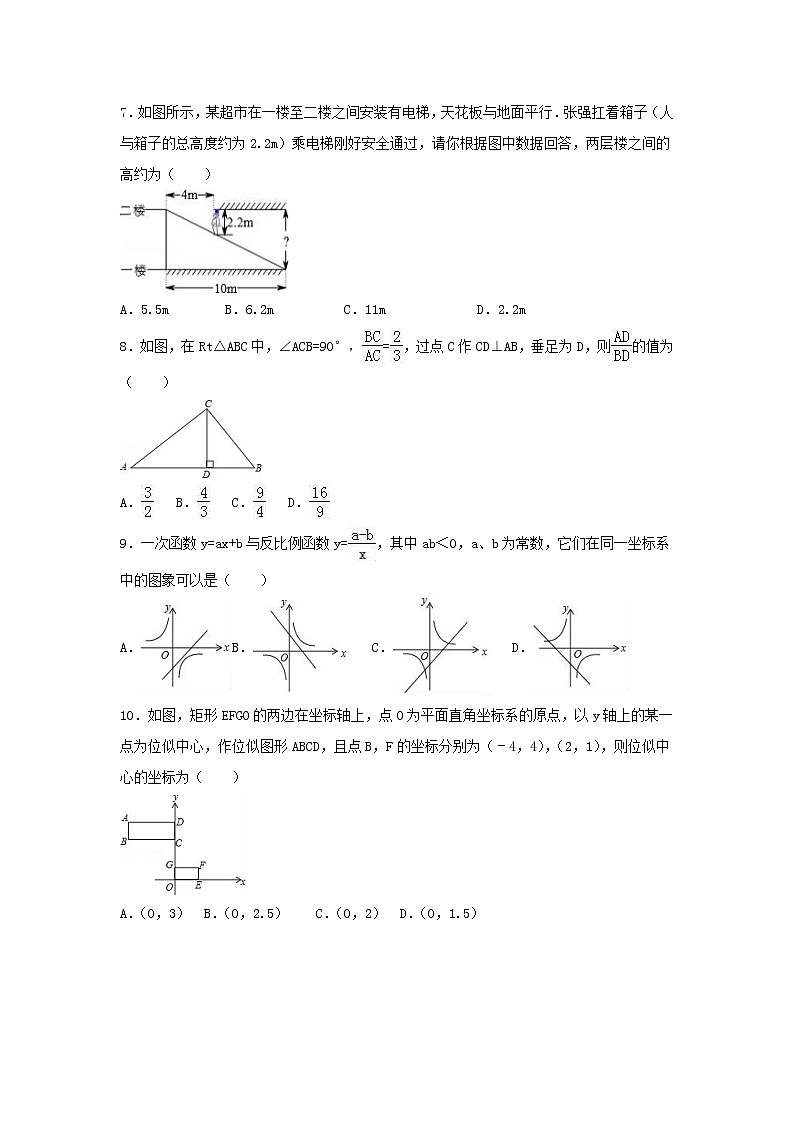
7．如图所示，某超市在一楼至二楼之间安装有电梯，天花板与地面平行．张强扛着箱子（人与箱子的总高度约为2.2m）乘电梯刚好安全通过，请你根据图中数据回答，两层楼之间的高约为（　　）

A．5.5m        B．6.2m         C．11m            D．2.2m

8．如图，在Rt△ABC中，∠ACB=90°，=，过点C作CD⊥AB，垂足为D，则的值为（　　）

A． B． C． D．

9．一次函数y=ax+b与反比例函数y=，其中ab＜0，a、b为常数，它们在同一坐标系中的图象可以是（　　）

A． B． C． D．

10．如图，矩形EFGO的两边在坐标轴上，点O为平面直角坐标系的原点，以y轴上的某一点为位似中心，作位似图形ABCD，且点B，F的坐标分别为（﹣4，4），（2，1），则位似中心的坐标为（　　）

A．（0，3） B．（0，2.5） C．（0，2） D．（0，1.5）

二、填空题

11．反比例函数y=的图象如图所示，则实数m的取值范围是　   　．

12．如图，在四个小正方体搭成的几何体中，每个小正方体的棱长都是1，则该几何体的三视图的面积之和是　   　．

13．如图，在反比例函数y=（x＞0）的图象上有点P1，P2，P3，P4，P5，它们的横坐标依次为2，4，6，8，10，分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1，S2，S3，S4，则S1+S2+S3+S4=　   　．

14．如图，在矩形ABCD中，AB=12，BC=9，点E，G分别为边AB，AD上的点，若矩形AEFG与矩形ABCD相似，且相似比为，连接CF，则CF=　   　．

三、解答题

15．解方程：x2﹣2x=x﹣2．

16．小玲用下面的方法来测量学校教学大楼AB的高度：如图，在水平面上放一面平面镜，镜子与教学楼的距离EA=12米，当她与镜子的距离CE=2米时，她刚好能从镜子中看到教学楼的顶端B．已知她的眼睛距地面的高度DC=1.5米．请你帮助小玲计算出教学楼的高度AB是多少米（根据光的反射定律：反射角等于入射角．）

17．锐锐参加我市电视台组织的“牡丹杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有3个选项，第二道单选题有4个选项，这两道题锐锐都不会，不过锐锐还有两个“求助”可以用（使用“求助”一次可以让主持人去掉其中一题的一个错误选项）．

（1）如果锐锐两次“求助”都在第一道题中使用，那么锐锐通关的概率是　   　．

（2）如果锐锐两次“求助”都在第二道题中使用，那么锐锐通关的概率是　   　．

（3）如果锐锐将每道题各用一次“求助”，请用树状图或者列表来分析他顺利通关的概率．

18．如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为点E，连接AE，F为AE上一点，且∠BFE=∠C．

（1）求证：△ABF∽△EAD．

（2）若AE=4，∠BAE=30°，求AB的长．

19．如图，在矩形ABCD中，E，F分别为边AD，BC上的点，AE=CF，对角线AC平分∠ECF．

（1）求证：四边形AECF为菱形．

（2）已知AB=4，BC=8，求菱形AECF的面积．

20．如图，一次函数y1=kx+b（k，b为常数，且k≠0）与反比例函数y2=（m为常数，且m≠1）的交点为A（1，3），与x轴的正半轴交于点B．

（1）求反比例函数的解析式；

（2）若△AOB的面积为6，求直线AB的解析式；

（3）若y1＞y2，求x的取值范围．

21.小武家的空气湿度指数为20%RH，通电开机后，空气湿度调节器自动开始增加空气湿度，此过程中空气湿度指数y（%RH）与开机时间x（分钟）满足一次函数关系，当空气的湿度指数到70%RH时空气湿度调节器会自动停止工作，随后空气湿度指数开始下降，此过程中空气湿度指数y（%RH）与开机时间x（分钟）成反比例关系，当空气湿度指数为20%RH时，空气湿度调节器又自动开始增加空气湿度…，重复上述程序（如图），根据图中提供的信息，解答下列问题：

（1）若0≤x≤10，求空气湿度指数y（%RH）与开机时间x（分钟）的函数关系式；

（2）求图中t的值；

（3）若小武在通电开机后即外出散步，请你预测小武散步1小时回到家时，屋内的空气湿度指数约为多少？

22．在Rt△ABC中，∠BAC=90°，过点B的直线MN∥AC，D为BC边上一动点，连接AD，作DE⊥AD交MN于点E，连接AE．

（1）如图1．当AD=DE时，求证：AB=AC．

（2）如图2，当DE：AD=：1时，线段AB与AC有何数量关系？请说明理由．

23．如图，在直角坐标系中，Rt△ABC的直角边AC在x轴上，∠ACB=90°，AC=1，反比例函数y=（k＞0）的图象经过BC边的中点D（3，1）．

（1）求这个反比例函数的表达式；

（2）若△ABC与△EFG成中心对称，且△EFG的边FG在y轴的正半轴上，点E在这个函数的图象上．

①求OF的长；

②连接AF，BE，证明四边形ABEF是正方形．

参考答案

1．故选：D．

2．故选：A．

3．故选：D．

4．故选：A．

5．故选：B．

6．故选：C．

7．故选：A．

8．故选：C．

9．故选：C．

10．故选：C．

11．答案为m＞1．

12．答案为：9．

13．答案为：4

14．答案为：5或．

15．解：方程整理，得

x（x﹣2）﹣（x﹣2）=0，

因式分解，得（x﹣2）（x﹣1）=0

于是，得x﹣2=0或x﹣1=0解得x1=2，x2=1．

16．解：∵由题意得，∠AEB=∠CED，∠BAE=∠DCE=90°，

∴△ABE∽△CDE，

∴=，即=，∴AB=9（米）．

答：教学大楼的高度AB是9米．

17．解：（1）第一道肯定能对，第二道对的概率为，

所以锐锐通关的概率为；故答案为：；

（2）锐锐两次“求助”都在第二道题中使用，

则第一道题对的概率为，第二道题对的概率为，

所以锐锐能通关的概率为×=；故答案为：；

（3）锐锐将每道题各用一次“求助”，分别用A，B表示剩下的第一道单选题的2个选项，a，b，c表示剩下的第二道单选题的3个选项，

树状图如图所示：共有6种等可能的结果，锐锐顺利通关的只有1种情况，

∴锐锐顺利通关的概率为：．

18．（1）证明：∵AD∥BC，

∴∠C+∠ADE=180°．

∵∠BFE=∠C，

∴∠AFB=∠EDA．

∵AB∥DC，

∴∠BAE=∠AED．

∴△ABF∽△EAD．

（2）∵AB∥CD，BE⊥CD，

∴∠ABE=90°，

∵AE=4，∠BAE=30°，

∴BE=2，

∴AB=．

19.（1）证明：由矩形可得：OA=OC，EF⊥AC，

∴AF=CF，

∵四边形ABCD是矩形，

∴AD∥BC，

∴∠FAC=∠ECA，

在△AOF和△COE中，

，

∴△AOF≌△COE（ASA），

∴OE=OF，

∴四边形AECF是平行四边形，

∵AF=CF，

∴四边形AECF是菱形；

（2）设CE=x，则AE=x，be=8﹣x，

∵四边形ABCD是矩形，

∴∠B=90°，

∴BE2+AB2=AE2，

∴（8﹣x）2+42=x2，

解得：x=5，即EC=5，

∴S菱形AECF=EC•AB=5×4=20．

20．解：（1）∵反比例函数y2=（m为常数，且m≠1）经过A（1，3），

∴3=，解得：m=4，∴反比例函数的解析式是y=；

（2）设B（a，0），则BO=a，

∵A（1，3），△AOB的面积为6，

∴a×3=6，解得：a=4，∴B（4，0），

∵一次函数y1=kx+b的图象过A、B两点，A（1，3），

∴代入得：，解得：k=﹣1，b=4，

∴直线AB的解析式为y=﹣x+4；

（3）由解得：或，

即一次函数与反比例函数的交点坐标为（1，3），（3，1），

由图象可知：若y1＞y2，则x的取值范围是1＜x＜3．

21．解：（1）当0≤x≤10时，设空气湿度指数y（%RH）与开机时间x（分钟）的函数关系式为：y=kx+b，

根据题意可得：，解得：，

∴函数关系式为：y=5x+20；

（2）在湿度的下降的过程中，设空气湿度指数y（%RH）与开机时间x（分钟）的函数关系式为：y=，根据题意可得：70=，即n=700，

故y=，当y=20时，20=，解得：t=35；

（3）∵60﹣35=25＞10，∴当x=25时，y==28，

答：小武散步1小时回到家时，屋内的空气湿度约为28%RH．

22．（1）证明：如图1中，作DF⊥BC交AB于F．则∠BDE+∠FDE=90°，

∵DE⊥AD，

∴∠FDE+∠ADF=90°，

∴∠BDE=∠ADF，

∵∠BAC=∠CDF=90°，

∴∠C+∠AFD=180°，

∵MN∥AC，

∴∠C+∠EBD=180°，

∴∠EBD=∠AFD，

在△BDE和△FDA中，

，

∴△BDE≌△FDA，

∴BD=DF，

∵∠BDF=90°，

∴∠ABC=45°，

∴∠ABC=∠C=45°，

∴AB=AC．

（2）结论：AB=AC．

理由：作DG⊥BC于G，则∠BDE+∠GDE=90°，

∵DE⊥AD，

∴∠GDE+∠ADG=90°，

∴∠BDE=∠ADG，

∵MN∥AC，

∴∠EBA=∠BAC=90°，

∵∠EBD=90°+∠ABC，∠AGD=∠ABC+∠BDG=∠ABC+90°，

∴∠EBD=∠AGD，

∴△BDE∽△GDA，

∴=，∵DE：AD=：1，∴=，

∵∠BDG=∠BAC=90°，∴△BDG∽△BAC，

∴=，∴==．

23．解：

（1）∵反比例函数y=（k＞0）的图象经过点D（3，1），

∴k=3×1=3，∴反比例函数表达式为y=；

（2）①∵D为BC的中点，

∴BC=2，

∵△ABC与△EFG成中心对称，

∴△ABC≌△EFG，

∴GF=BC=2，GE=AC=1，

∵点E在反比例函数的图象上，

∴E（1，3），即OG=3，

∴OF=OG﹣GF=1；

②如图，连接AF、BE，

∵AC=1，OC=3，∴OA=GF=2，

在△AOF和△FGE中

∴△AOF≌△FGE（SAS），

∴∠GFE=∠FAO=∠ABC，

∴∠GFE+∠AFO=∠FAO+∠BAC=90°，

∴EF∥AB，且EF=AB，

∴四边形ABEF为平行四边形，

∴AF=EF，

∴四边形ABEF为菱形，

∵AF⊥EF，

∴四边形ABEF为正方形．