2020版数学（理）新设计大一轮人教A版新高考（鲁津京琼）讲义：第四章三角函数、解三角形第2节

第2节　同角三角函数基本关系式与诱导公式
考试要求　1.理解同角三角函数的基本关系式：sin2α＋cos2α＝1，＝tan α；2.能利用定义推导出诱导公式.

知 识 梳 理
1.同角三角函数的基本关系
(1)平方关系：sin2α＋cos2α＝1.
(2)商数关系：＝tan__α.
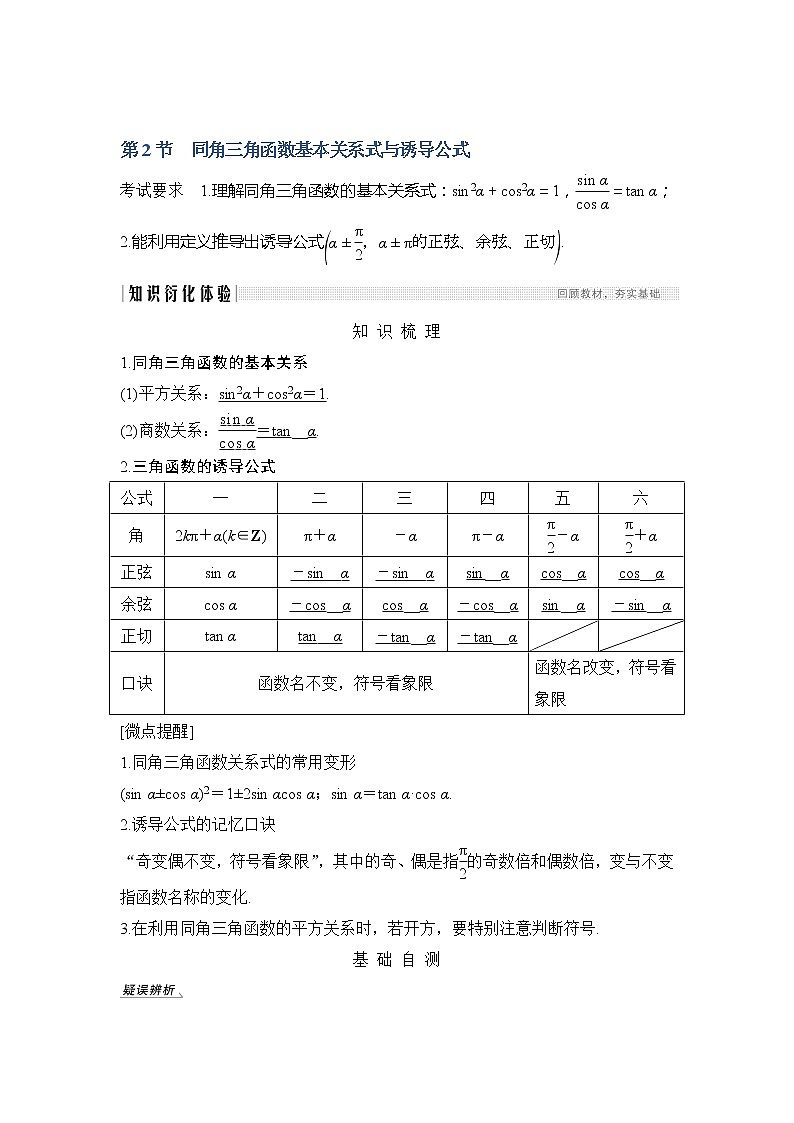
2.三角函数的诱导公式
公式
一
二
三
四
五
六
角
2kπ＋α(k∈Z)
π＋α
－α
π－α
－α
＋α
正弦
sin α
－sin__α
－sin__α
sin__α
cos__α
cos__α
余弦
cos α
－cos__α
cos__α
－cos__α
sin__α
－sin__α
正切
tan α
tan__α
－tan__α
－tan__α


口诀
函数名不变，符号看象限
函数名改变，符号看象限
[微点提醒]
1.同角三角函数关系式的常用变形
(sin α±cos α)2＝1±2sin αcos α；sin α＝tan α·cos α.
2.诱导公式的记忆口诀
“奇变偶不变，符号看象限”，其中的奇、偶是指的奇数倍和偶数倍，变与不变指函数名称的变化.
3.在利用同角三角函数的平方关系时，若开方，要特别注意判断符号.
基 础 自 测

1.判断下列结论正误(在括号内打“√”或“×”)
(1)sin(π＋α)＝－sin α成立的条件是α为锐角.(　　)
(2)六组诱导公式中的角α可以是任意角.(　　)
(3)若α∈R，则tan α＝恒成立.(　　)
(4)若sin(kπ－α)＝(k∈Z)，则sin α＝.(　　)
解析　(1)中对于任意α∈R，恒有sin(π＋α)＝－sin α.
(3)中当α的终边落在y轴，商数关系不成立.
(4)当k为奇数时，sin α＝，
当k为偶数时，sin α＝－.
答案　(1)×　(2)√　(3)×　(4)×

2.(必修4P21A12改编)已知tan α＝－3，则cos2α－sin2α＝(　　)
A. B.－ C. D.－
解析　由同角三角函数关系得
cos2α－sin2α＝＝＝＝－.
答案　B
3.(必修4P29B2改编)已知α为锐角，且sin α＝，则cos (π＋α)＝(　　)
A.－ B. C.－ D.
解析　因为α为锐角，所以cos α＝＝，
故cos(π＋α)＝－cos α＝－.
答案　A

4.(2017·全国Ⅲ卷)已知sin α－cos α＝，则sin 2α＝(　　)
A.－ B.－ C. D.
解析　∵(sin α－cos α)2＝1－2sin αcos α＝1－sin 2α，
∴sin 2α＝1－＝－.
答案　A
5.(2019·济南质检)若sin α＝－，且α为第四象限角，则tan α＝(　　)
A. B.－ C. D.－
解析　∵sin α＝－，α为第四象限角，
∴cos α＝＝，因此tan α＝＝－.
答案　D
6.(2018·上海嘉定区月考)化简：＝________.
解析　原式＝＝＝1.
答案　1

考点一　同角三角函数基本关系式　多维探究
角度1　公式的直接运用
【例1－1】 (2018·延安模拟)已知α∈，且sin α＝－，则cos α＝(　　)
A.－ B. C.± D.
解析　因为α∈，且sin α＝－>－＝sin，所以α为第三象限角，所以cos α＝－＝－＝－.
答案　A
角度2　关于sin α，cos α的齐次式问题
【例1－2】 已知＝－1，求下列各式的值.
(1)；
(2)sin2α＋sin αcos α＋2.
解　由已知得tan α＝.
(1)＝＝－.
(2)sin2α＋sin αcos α＋2＝＋2＝＋2＝＋2＝.
角度3　“sin α±cos α，sin αcos α”之间的关系
【例1－3】 已知x∈(－π，0)，sin x＋cos x＝.
(1)求sin x－cos x的值；
(2)求的值.
解　(1)由sin x＋cos x＝，
平方得sin2x＋2sin xcos x＋cos2x＝，
整理得2sin xcos x＝－.
所以(sin x－cos x)2＝1－2sin xcos x＝.
由x∈(－π，0)，知sin x<0，又sin x＋cos x>0，
所以cos x>0，则sin x－cos x<0，
故sin x－cos x＝－.
(2)＝
＝＝＝－.
规律方法　1.同角三角函数关系的用途：根据已知角的一个三角函数值求解另外的三角函数值，对三角函数式进行变换.(1)利用sin2α＋cos2α＝1可以实现角α的正弦、余弦的互化.(2)利用＝tan α可以实现角α的弦切互化.
2.应用公式时注意方程思想的应用：对于sin α＋cos α，sin αcos α，sin α－cos α这三个式子，利用(sin α±cos α)2＝1±2sin αcos α，可以知一求二.
3.注意公式逆用及变形应用：1＝sin2α＋cos2α，sin2α＝1－cos2α，cos2α＝1－sin2α.
【训练1】 (1)(2019·烟台测试)已知sin αcos α＝，且<α<，则cos α－sin α的值为(　　)
A.－ B. C.－ D.
(2)已知＝5，则cos2α＋sin 2α的值是(　　)
A. B.－ C.－3 D.3
解析　(1)∵<α<，
∴cos α<0，sin α<0且cos α>sin α，
∴cos α－sin α>0.
又(cos α－sin α)2＝1－2sin αcos α＝1－2×＝，
∴cos α－sin α＝.
(2)由＝5得＝5，可得tan α＝2，
则cos2α＋sin 2α＝cos2α＋sin αcos α＝＝＝.
答案　(1)B　(2)A
考点二　诱导公式的应用
【例2】 (1)设f(α)＝(1＋2sin α≠0)，则f＝________.
(2)已知cos＝a，则cos＋sin的值是________.
解析　(1)∵f(α)＝
＝＝＝，
∴f＝＝＝.
(2)∵cos＝cos
＝－cos＝－a，
sin＝sin＝a，
∴cos＋sin＝－a＋a＝0.
答案　(1)　(2)0
规律方法　1.诱导公式的两个应用
(1)求值：负化正，大化小，化到锐角为终了.
(2)化简：统一角，统一名，同角名少为终了.
2.含2π整数倍的诱导公式的应用
由终边相同的角的关系可知，在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算，如cos(5π－α)＝cos(π－α)＝－cos α.
【训练2】 (1)(2019·衡水中学调研)若cos＝，则cos(π－2α)＝(　　)
A. B. C.－ D.－
(2)(2017·北京卷)在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称.若sin α＝，则sin β＝________.
解析　(1)由cos＝，得sin α＝.
∴cos(π－2α)＝－cos 2α＝－(1－2sin2α)＝2sin2α－1＝2×－1＝－.
(2)α与β的终边关于y轴对称，则α＋β＝π＋2kπ，k∈Z，
∴β＝π－α＋2kπ，k∈Z.
∴sin β＝sin(π－α＋2kπ)＝sin α＝.
答案　(1)D　(2)
考点三　同角三角函数基本关系式与诱导公式的综合应用
【例3】 (1)(2019·菏泽联考)已知α∈，sin＝，则tan(π＋2α)＝(　　)
A. B.± C.± D.
(2)(2019·福建四地六校联考)已知α为锐角，且2tan(π－α)－3cos＋5＝0，tan(π＋α)＋6sin(π＋β)－1＝0，则sin α的值是(　　)
A. B. C. D.
解析　(1)∵α∈，sin＝，
∴cos α＝，sin α＝－，tan α＝＝－2.
∴tan(π＋2α)＝tan 2α＝＝＝.
(2)由已知得
消去sin β，得tan α＝3，
∴sin α＝3cos α，代入sin2α＋cos2α＝1，
化简得sin2α＝，则sin α＝(α为锐角).
答案　(1)A　(2)C
(3)已知－π ①求sin x－cos x的值；
②求的值.
解　①由已知，得sin x＋cos x＝，
两边平方得sin2x＋2sin xcos x＋cos2 x＝，
整理得2sin xcos x＝－.
∵(sin x－cos x)2＝1－2sin xcos x＝，
由－π 又sin xcos x＝－<0，
∴cos x>0，∴sin x－cos x<0，
故sin x－cos x＝－.
②＝
＝
＝＝－.
规律方法　1.利用同角三角函数关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形.
2.(1)注意角的范围对三角函数值符号的影响，开方时先判断三角函数值的符号；
(2)熟记一些常见互补的角、互余的角，如－α与＋α互余等.
【训练3】 (1)(2019·湖北七州市联考)已知α∈(0，π)，且cos α＝－，则sin·tan α＝(　　)
A.－ B.－ C. D.
(2)已知θ是第四象限角，且sin＝，则tan＝________.
解析　(1)∵α∈(0，π)，且cos α＝－，∴sin α＝，
因此sin·tan α＝cos α·＝sin α＝.
(2)由题意，得cos＝，∴tan＝.
∴tan＝tan＝－＝－.
答案　(1)C　(2)－

[思维升华]
1.同角三角函数基本关系可用于统一函数；诱导公式主要用于统一角，其主要作用是进行三角函数的求值、化简和证明.
2.三角函数求值、化简的常用方法：(1)弦切互化法：主要利用公式tan x＝进行切化弦或弦化切，如，asin2x＋bsin xcos x＋ccos2x等类型可进行弦化切.
(2)和积转换法：如利用(sin θ±cos θ)2＝1±2sin θcos θ的关系进行变形、转化.
(3)巧用“1”的变换：1＝sin2θ＋cos2θ＝cos2θ(1＋tan2θ)＝sin2θ(1＋)＝tan 等.
[易错防范]
1.利用诱导公式进行化简求值时，可利用公式化任意角的三角函数为锐角三角函数，其步骤：去负—脱周—化锐.
特别注意函数名称和符号的确定.
2.注意求值与化简后的结果一般要尽可能有理化、整式化.

基础巩固题组
(建议用时：35分钟)
一、选择题
1.sin 600°的值为(　　)
A.－ B.－ C. D.
解析　sin 600°＝sin(360°＋240°)＝sin 240°
＝sin(180°＋60°)＝－sin 60°＝－.
答案　B
2.已知直线2x－y－1＝0的倾斜角为α，则sin 2α－2cos2α＝(　　)
A. B.－ C.－ D.－
解析　由题意知tan α＝2，
∴sin 2α－2cos2α＝＝＝.
答案　A
3.＝(　　)
A.sin 2－cos 2 B.sin 2＋cos 2
C.±(sin 2－cos 2) D.cos 2－sin 2
解析　＝
＝＝|sin 2－cos 2|＝sin 2－cos 2.
答案　A
4.已知sin(π＋θ)＝－cos(2π－θ)，|θ|<，则θ等于(　　)
A.－ B.－ C. D.
解析　∵sin(π＋θ)＝－cos(2π－θ)，
∴－sin θ＝－cos θ，
∴tan θ＝，∵|θ|＜，∴θ＝.
答案　D
5.已知sin＝，则cos＝(　　)
A. B. C.－ D.－
解析　因为sin＝，所以cos＝sin＝sin＝.
答案　B
6.(2019·兰州质检)向量a＝，b＝(cos α，1)，且a∥b，则cos＝(　　)
A.－ B. C.－ D.－
解析　∵a＝，b＝(cos α，1)，且a∥b，
∴×1－tan αcos α＝0，∴sin α＝，
∴cos＝－sin α＝－.
答案　A
7.已知函数f(x)＝asin(πx＋α)＋bcos(πx＋β)，且f(4)＝3，则f(2 020)的值为(　　)
A.－1 B.1 C.3 D.－3
解析　∵f(4)＝asin(4π＋α)＋bcos(4π＋β)
＝asin α＋bcos β＝3，
∴f(2 020)＝asin(2 020π＋α)＋bcos(2 020π＋β)
＝asin α＋bcos β＝3.
答案　C
二、填空题
8.(2019·广东七校联考)已知sin α＝－，且α为第三象限的角，则tan α＝________.
解析　∵sin α＝－，且α为第三象限的角，
∴cos α＝－＝－，∴tan α＝＝.
答案　
9.已知tan＝，则tan＝________.
解析　∵＋＝π，
∴tan＝tan
＝－tan＝－.
答案　－
10.已知sin θ＋cos θ＝，θ∈，则sin θ－cos θ的值为________.
解析　∵sin θ＋cos θ＝，∴sin θcos θ＝.
又∵(sin θ－cos θ)2＝1－2sin θcos θ＝，
又∵θ∈，∴sin θ－cos θ＝－.
答案　－
11.已知tan θ＝3，则cos＝________.
解析　∵tan θ＝3，∴cos＝sin 2θ＝＝＝＝.
答案　
12.(2019·邯郸一模)若sin(α＋β)＝3sin(π－α＋β)，且α，β∈，则＝________.
解析　由条件，得sin(α＋β)＝3sin(α－β)，
∴sin αcos β＝2cos αsin β，则tan α＝2tan β，
因此＝2.
答案　2
能力提升题组
(建议用时：15分钟)
13.若sin θ，cos θ是方程4x2＋2mx＋m＝0的两根，则m的值为(　　)
A.1＋ B.1－
C.1± D.－1－
解析　由题意知sin θ＋cos θ＝－，sin θ·cos θ＝.
又＝1＋2sin θcos θ，
∴＝1＋，解得m＝1±.
又Δ＝4m2－16m≥0，∴m≤0或m≥4，∴m＝1－.
答案　B
14.已知sincos＝，且0<α<，则sin α＝________，cos α＝________.
解析　sincos＝－cos α·(－sin α)＝sin αcos α＝.
∵0<α<，∴0 又∵sin2α＋cos2α＝1，∴sin α＝，cos α＝.
答案　　
15.已知k∈Z，化简：＝________.
解析　当k＝2n(n∈Z)时，
原式＝
＝＝＝－1；
当k＝2n＋1(n∈Z)时，
原式＝
＝＝＝－1.
综上，原式＝－1.
答案　－1
16.是否存在α∈，β∈(0，π)，使等式sin(3π－α)＝cos，cos(－α)＝－cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，请说明理由.
解　假设存在角α，β满足条件，
则由已知条件可得
由①2＋②2，得sin2α＋3cos2α＝2.
∴sin2α＝，∴sin α＝±.
∵α∈，∴α＝±.
当α＝时，由②式知cos β＝，
又β∈(0，π)，∴β＝，此时①式成立；
当α＝－时，由②式知cos β＝，
又β∈(0，π)，∴β＝，此时①式不成立，故舍去.
∴存在α＝，β＝满足条件.
新高考创新预测
17.(多填题)已知sin α＝，α∈，则cos(π－α)＝________，cos 2α＝________.
解析　cos(π－α)＝－cos α＝－＝－，cos 2α＝cos2α－sin2α＝－＝.
答案　－