北师大版2021年中考数学总复习《勾股定理》（含答案） 试卷

北师大版2021年中考数学总复习

《勾股定理》

一         、选择题

1.若直角三角形的三边长分别为2，4，x，则x的值可能有(    )．

A.1个    B.2个          C.3个      D.4个

2.下列四组数分别表示三角形的三条边长，其中能构成直角三角形的是（　　）

A.2、3、4                    B.2、3、                      C.、、                         D.1、1、2

3.下列条件中，不能判断一个三角形是直角三角形的是(　　）

A．三个角的比为1：2：3  

B．三条边满足关系a2=b2﹣c2

C．三条边的比为1：2：3  

D．三个角满足关系∠B+∠C=∠A

4.如图，线段AB=、CD=，那么，线段EF的长度为（　　）

A．      B．      C．      D．

5.如图所示，AB=BC=CD=DE=1，AB⊥BC，AC⊥CD，AD⊥DE，则AE=（　　）

A.1         B.          C.            D.2  

6.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是(    )

    A.48                B.60           C.74                 D.80

7.如图，在△ABC中，点D，E分别是边AB，AC的中点，AF⊥BC，垂足为点F，∠ADE=30°，DF=4，则BF的长为（　　）

A.4          B.8      C.2        D.4

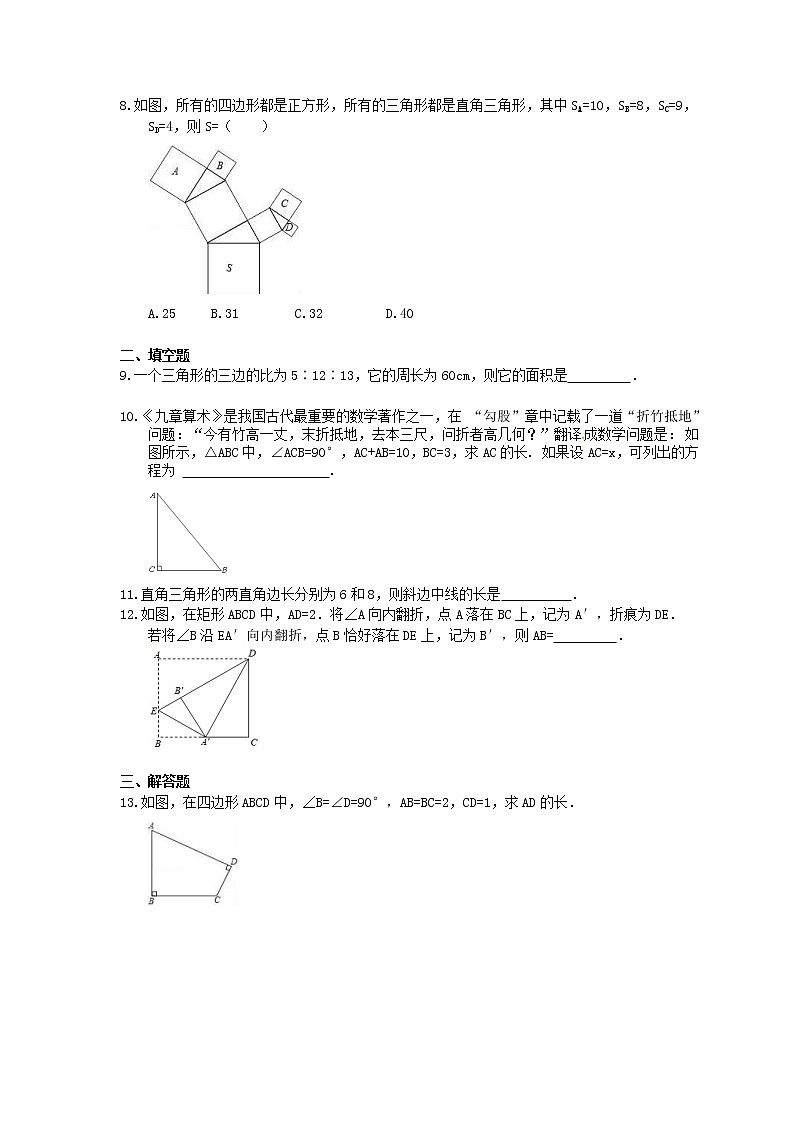
8.如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中SA=10，SB=8，SC=9，SD=4，则S=（　　）

A.25                   B.31                      C.32                       D.40

二         、填空题

9.一个三角形的三边的比为5∶12∶13，它的周长为60cm，则它的面积是     ．

10.《九章算术》是我国古代最重要的数学著作之一，在 “勾股”章中记载了一道“折竹抵地”问题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何？”翻译成数学问题是： 如图所示，△ABC中，∠ACB=90°，AC+AB=10，BC=3，求AC的长. 如果设AC=x，可列出的方程为                      .

11.直角三角形的两直角边长分别为6和8，则斜边中线的长是　　      ．

12.如图，在矩形ABCD中，AD=2．将∠A向内翻折，点A落在BC上，记为A′，折痕为DE．

若将∠B沿EA′向内翻折，点B恰好落在DE上，记为B′，则AB=　   　．

三         、解答题

13.如图，在四边形ABCD中，∠B=∠D=90°，AB=BC=2，CD=1，求AD的长．

14.如图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，求：

(1)边AC，AB，BC的长;(2)点C到AB边的距离；(3)求△ABC的面积。

15.如图，已知△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．

（1）求证：△ACE≌△BCD；

（2）求证：2CD2=AD2+DB2．

16.阅读下列解题过程：

已知a,b,c为△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状．

   解：因为a2c2-b2c2=a4-b4， ①

       所以c2(a2-b2)=(a2-b2)(a2+b2) ②

       所以c2=a2+b2．③

       所以△ABC是直角三角形.④

回答下列问题：

（1）上述解题过程，从哪一步开始出现错误?该步的序号为            .

（2）错误的原因为               .

（3）请你将正确的解答过程写下来.

参考答案

1.B．

2.C.

3.答案为：C.

4.C．

5.D

6.C

7.答案为：D；

8.B

9.答案为：120 cm2.

10.答案为：x2+9=(10-x)2.

11.答案为：5．

12.答案为：．

13.解：连接AC，

∵∠B=90°

∴AC2=AB2+BC2．

∵AB=BC=2

∴AC2=8．

∵∠D=90°

∴AD2=AC2﹣CD2．

∵CD=1，

∴AD2=7．

∴．

14.1）AC=，AB=，BC=；（2）点C到AB的距离是；（3）。

15.证明：（1）∵△ABC和△ECD都是等腰直角三角形，∴AC=BC，CD=CE，

∵∠ACB=∠DCE=90°，∴∠ACE+∠ACD=∠BCD+∠ACD，∴∠ACE=∠BCD，

在△ACE和△BCD中，，∴△AEC≌△BDC（SAS）；

 （2）∵△ACB是等腰直角三角形，∴∠B=∠BAC=45度．

∵△ACE≌△BCD，∴∠B=∠CAE=45°

∴∠DAE=∠CAE+∠BAC=45°+45°=90°，∴AD2+AE2=DE2．

由（1）知AE=DB，∴AD2+DB2=DE2，即2CD2=AD2+DB2．

16.（1）③ 

（2）忽略了a2-b2=0的可能

（3）解：因为a2c2-b2c2=a4-b4，所以c2(a2-b2)=(a2-b2)(a2+b2), 所以a=b或c2=a2+b2．

     所以△ABC是等腰三角形或直角三角形.