初中数学北师大版九年级上册2 反比例函数的图象与性质教案配套ppt课件

这是一份初中数学北师大版九年级上册2 反比例函数的图象与性质教案配套ppt课件，共18页。PPT课件主要包含了不存在，平方根的表达式为，即16的平方根是，a的平方根记作，的平方根是，负数不存在平方根，另一个是-，它们互为相反数，负数没有平方根，没意义等内容，欢迎下载使用。

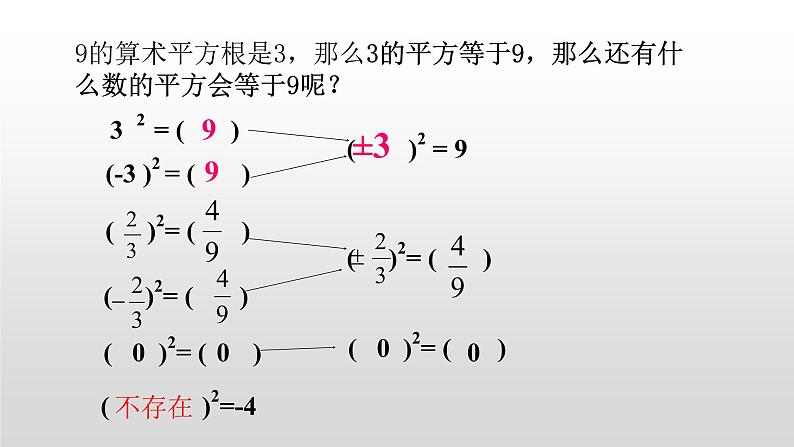
9的算术平方根是3，那么3的平方等于9，那么还有什么数的平方会等于9呢？
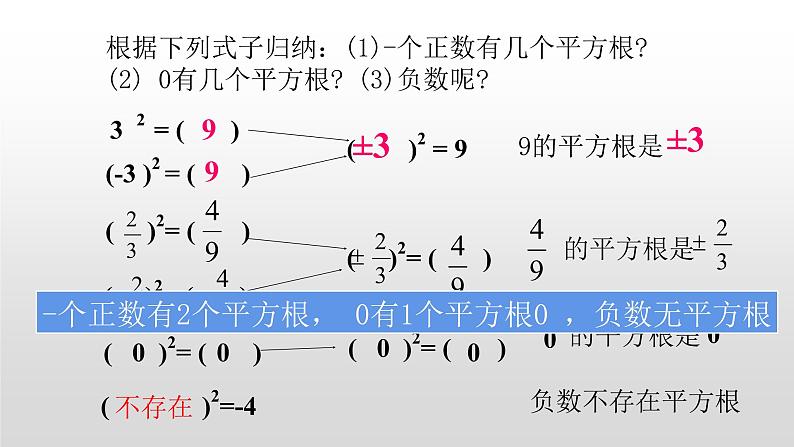
3 2 = ( )
(-3 )2 = ( )
( )2 = 9
( 0 )2= ( )
( )2= ( )
( )2=-4
一般地，如果一个数的平方等于a，那么这个数叫做a的平方根或二次方根.而把正的平方根叫算术平方根.
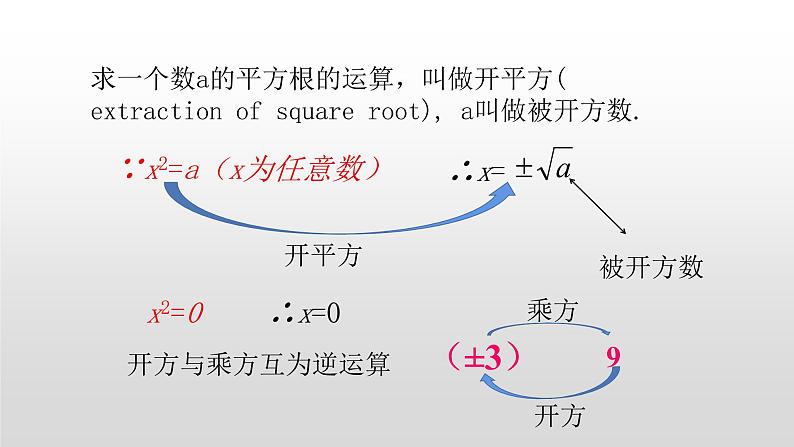
∵x2=a（x为任意数）
例如:(±4)2=16,则+4和-4都是16的平方根;
+4是16的算术平方根.
根据下列式子归纳：(1)-个正数有几个平方根? (2) 0有几个平方根? (3)负数呢?
-个正数有2个平方根， 0有1个平方根0 ，负数无平方根
这两个平方根合起来可以记作 ， 读作“正、负根号a”.
正数a有两个平方根，一个是a的算术平方根
求一个数a的平方根的运算，叫做开平方( extractin f square rt), a叫做被开方数.
联系：1.包含关系：平方根包含算术平方根，算术平方根是平方根的一种.
2.只有非负数才有平方根和算术平方根.
3. 0的平方根是0，算术平方根也是0 .
1.个数不同：一个正数有两个平方根， 但只有一个算术平方根.
例1.求下列各数的平方根:
∴64的平方根为 ,
∴ 的平方根为 ,
(3) 0.0004
∴0.0004的平方根为 ,
所以(-25)2的平方根是±25
规律：(±25)2=(+25)2=(-25)2
11的平方根是 .
总结：运用平方运算求一个非负数的平方根是常 用的方法，如果被开方数是小数，要注意小数点的位置，也可先将小数化为分数， 再求它的平方根，如果被开方数是带分数，先要把它化为假分数.
一个正数正的平方根也叫算术平方根
=　　　，当a≥0时， =　　 . 
右边等式两边平方就得到左边式子
1. (-5)2的平方根是 , 的算术平方根是 ， 的平方根是 . 　　　　
2. = ， = ， = ，
= .
3.下列说法正确的是　　　　.①-3是 的一个平方根；②25的平方根是5；③-36的平方根是-6；④平方根等于0的数是0；⑤64的平方根是8.
5.求下列各式中的x:(1) x²=16 (2) （x-1）²=
1.平方根的概念：若x2=a，则x叫做a的平方根，x= .
2.平方根的个数：正数有2个平方根，0的平方根是0，负数没有平方根.
3.平方与开平方之间是互逆关系.4.求平方根的方法：求一个数的平方根就是转化为寻找哪个数的平方等于这个数.
解析　由题中数轴易知a<0,b>0,且|b|>|a|,∴a+b>0.∴原式=-a+a+b-b=0.