初中数学北师大版九年级上册3 正方形的性质与判定教学演示课件ppt

这是一份初中数学北师大版九年级上册3 正方形的性质与判定教学演示课件ppt，共22页。PPT课件主要包含了邻边相等，有一个角是直角，所以正方形是菱形，所以正方形又是矩形，在正方形ABCD中，AC⊥BD，正方形，对角线，连接PCAC，∴APPC等内容，欢迎下载使用。

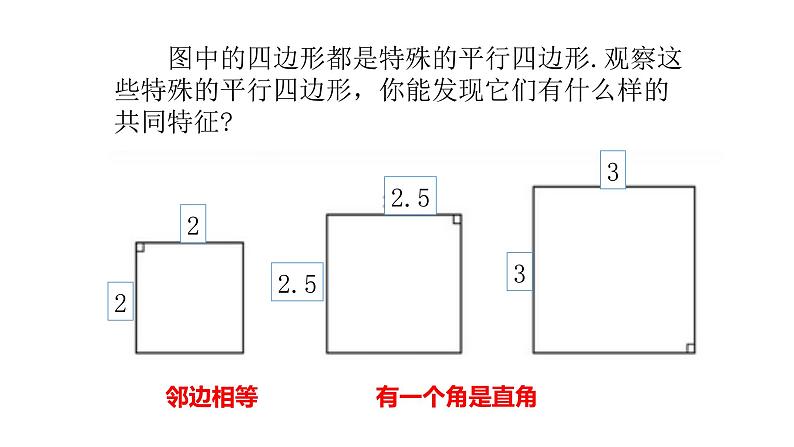
图中的四边形都是特殊的平行四边形.观察这些特殊的平行四边形，你能发现它们有什么样的共同特征?
有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形.
有一组邻边相等，平行四边形叫做菱形.
有一个角是直角的平行四边形叫做矩形.
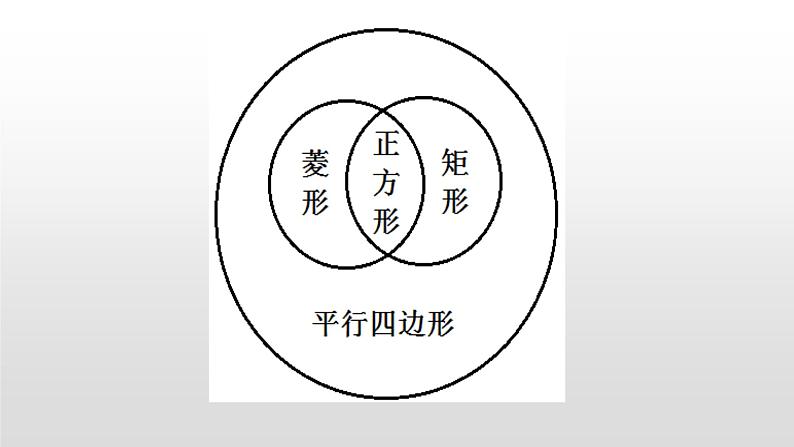
正方形既是矩形，又是菱形，它具有矩形与菱形的所有性质.
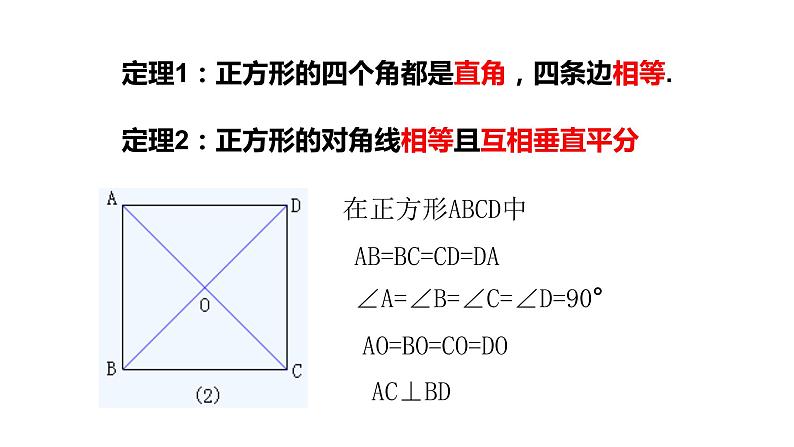
定理1：正方形的四个角都是直角，四条边相等.
定理2：正方形的对角线相等且互相垂直平分
AB=BC=CD=DA
∠A=∠B=∠C=∠D=90°
AO=BO=CO=DO
每条对角线平分一组对角
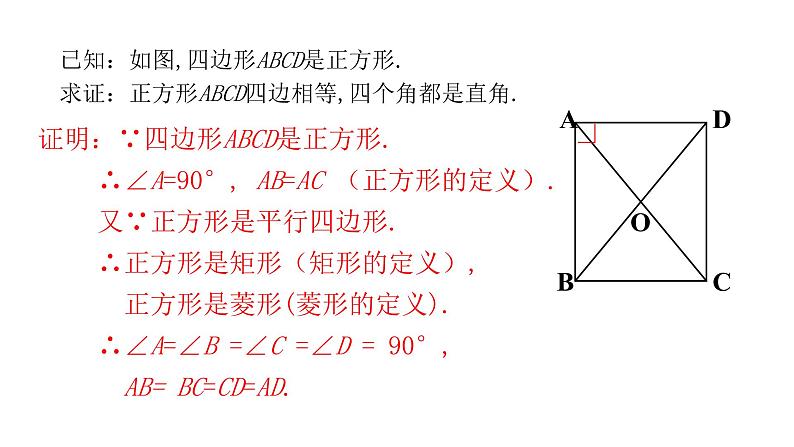
已知：如图,四边形ABCD是正方形.求证：正方形ABCD四边相等,四个角都是直角.
证明：∵四边形ABCD是正方形.∴∠A=90°, AB=AC （正方形的定义）. 又∵正方形是平行四边形.∴正方形是矩形（矩形的定义）, 正方形是菱形(菱形的定义).∴∠A=∠B =∠C =∠D = 90°, AB= BC=CD=AD.
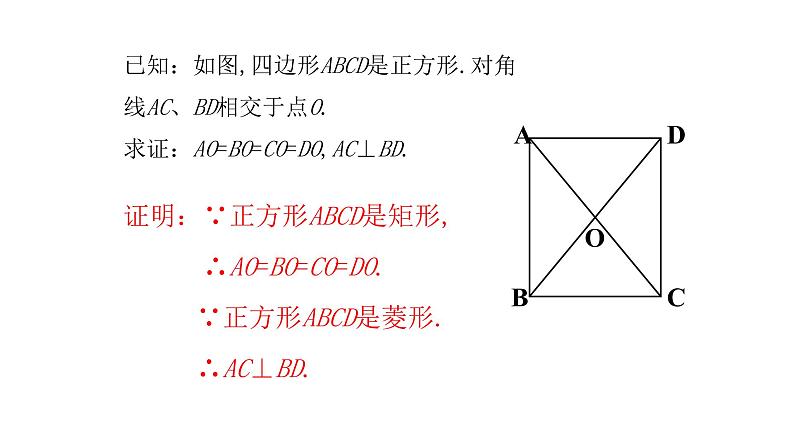
已知：如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证：AO=BO=CO=DO,AC⊥BD.
证明：∵正方形ABCD是矩形, ∴AO=BO=CO=DO. ∵正方形ABCD是菱形. ∴AC⊥BD.
例1：如图在正方形ABCD中,E为CD上一点，F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系？请说明理由.
解：BE=DF,且BE⊥DF.理由如下：（1）∵四边形ABCD是正方形.∴BC=DC,∠BCE =90° .（正方形的四条边都相等,四个角都是直角）∴∠DCF=180°-∠BCE=180°-90°=90°.
∴∠BCE=∠DCF.又∵CE=CF.
∴△BCE≌△DCF. BE=DF
(2)延长BE交DE于点M,∵△BCE≌△DCF ,∴∠CBE =∠CDF.∵∠DCF =90° ,∴∠CDF +∠F =90°.∴∠CBE+∠F=90° , ∴∠BMF=90°.∴BE⊥DF.
练习： 如图，在正方形ABCD中， ΔBEC是等边三角形， 求证： ∠EAD＝∠EDA＝15° .
证明：∵ ΔBEC是等边三角形，∴BE=CE=BC,∠EBC=∠ECB=60°，∵ 四边形ABCD是正方形，∴AB=BC=CD,∠ABC=∠DCB=90°，∴AB=BE=CE=CD, ∠ABE=∠DCE=30°，∴△ABE，△DCE是等腰三角形， ∴∠BAE=∠BEA=∠CDE=∠CED=75°，∴∠EAD=∠EDA=90°-75°=15°.
【变式题1】四边形ABCD是正方形，以正方形ABCD的一边作等边△ADE，求∠BEC的大小．
解：当等边△ADE在正方形ABCD外部时，如图①，AB＝AE，∠BAE＝90°＋60°＝150°.∴∠AEB＝15°.同理可得∠DEC＝15°.∴∠BEC＝60°－15°－15°＝30°；
当等边△ADE在正方形ABCD内部时，如图②，AB＝AE，∠BAE＝90°－60°＝30°，∴∠AEB＝75°.同理可得∠DEC＝75°.∴∠BEC＝360°－75°－75°－60°＝150°.综上所述，∠BEC的大小为30°或150°.
【变式题2】 如图，在正方形ABCD内有一点P满足AP=AB，PB=PC，连接AC、PD．（1）求证：△APB≌△DPC；
解：∵四边形ABCD是正方形，∴∠ABC=∠DCB=90°．∵PB=PC，∴∠PBC=∠PCB．∴∠ABC-∠PBC=∠DCB-∠PCB，即∠ABP=∠DCP．又∵AB=DC，PB=PC，∴△APB≌△DPC．
（2）求证：∠BAP=2∠PAC．
证明：∵四边形ABCD是正方形，∴∠BAC=∠DAC=45°．∵△APB≌△DPC，∴AP=DP．又∵AP=AB=AD，∴DP=AP=AD．∴△APD是等边三角形．∴∠DAP=60°．∴∠PAC=∠DAP-∠DAC=15°．∴∠BAP=∠BAC-∠PAC=30°．∴∠BAP=2∠PAC．
例2 如图，在正方形ABCD中，P为BD上一点，PE⊥BC于E， PF⊥DC于F.试说明：AP=EF.
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
又∵PE⊥BC ， PF⊥DC,
∴四边形PECF是矩形,
边： 正方形的对边平行且相等.
角： 正方形的四个角都是直角.
对角线： 正方形的两条对角线互相垂直平分且相等，每一条对角线平分一组对角.
习题1.7 1，2，3，4
例1：已知：如图，正方形ABCD中，对角线的交点为O，E是OB上的一点，DG⊥AE于G，DG交OA于F.求证：OE=OF.
∵四边形ABCD是正方形，
∴∠AOE=∠DOF=90°，AO=DO（正方形的对角线垂直平分且相等）
∴∠EAO+∠AEO=∠EDG+∠AEO=90°.
∴∠EAO=∠FDO.
∴△AEO≌△DFO.
例2：如图所示，在正方形ABCD中，点G是边BC上任意一点，DE⊥AG，垂足为点E，延长DE交AB于点F.在线段AG上取点H，使得AG=DE+HG，连接BH.求证：∠ABH=∠CDE.
正方形ABCD中，AB=AD，∠ABG=∠DAF=90°.
所以∠2+∠EAD=90°.
因为∠1+∠EAD=90°，
因为∠ABG=∠DAF=90°，
所以△ABG≌△DAF（ASA）.
所以BG=AF，AG=DF，∠BGA=∠AFD.
因为AG=DE+HG，DF=DE+EF.
所以△AEF≌△BHG（SAS）.
因为∠2+∠CDE=90°，∠3+∠ABH=90°，
所以∠ABH=∠CDE.
例3.（鄂州中考）如图正方形ABCD的边长为4，E、F分别为DC、BC中点.（1）求证：△ADE≌△ABF.（2）求△AEF的面积.
(1)因为四边形ABCD为正方形，
所以AB=AD，∠B=∠D=90°,DC=CB,
又因为E、F分别为DC、BC中点，
所以△ADE≌△ABF（SAS）.
（2）由题知△ABF、△ADE、△CEF均为直角三角形，
且AB=AD=4，DE=BF=12×4=2，CE=CF=12×4=2，
∴S△AEF =S正方形ABCD -S△ADE -S△ABF -S△CEF
=4×4- 0.5 ×4×2- 0.5×4×2- 0.5 ×2×2