北师大版2 矩形的性质与判定多媒体教学ppt课件

这是一份北师大版2 矩形的性质与判定多媒体教学ppt课件，共34页。PPT课件主要包含了三个角是直角，②对角线是不是相等，上述方法二和方法三，∴□ABCD是矩形，∴∠ABC90°，又∵AD＝AE，∴AE＝CF，∵AE＝CF，作业布置，选讲习题等内容，欢迎下载使用。
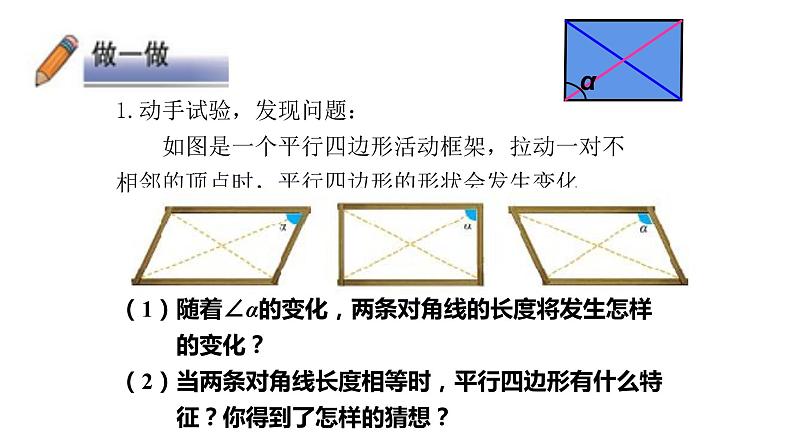
1.动手试验，发现问题： 如图是一个平行四边形活动框架，拉动一对不相邻的顶点时，平行四边形的形状会发生变化.
（1）随着∠α的变化，两条对角线的长度将发生怎样 的变化？（2）当两条对角线长度相等时，平行四边形有什么特 征？你得到了怎样的猜想？
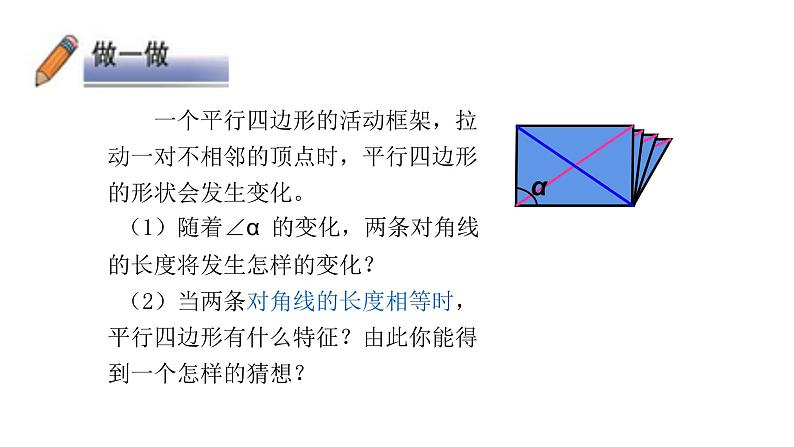
一个平行四边形的活动框架，拉动一对不相邻的顶点时，平行四边形的形状会发生变化。 （1）随着∠α 的变化，两条对角线的长度将发生怎样的变化？ （2）当两条对角线的长度相等时，平行四边形有什么特征？由此你能得到一个怎样的猜想？
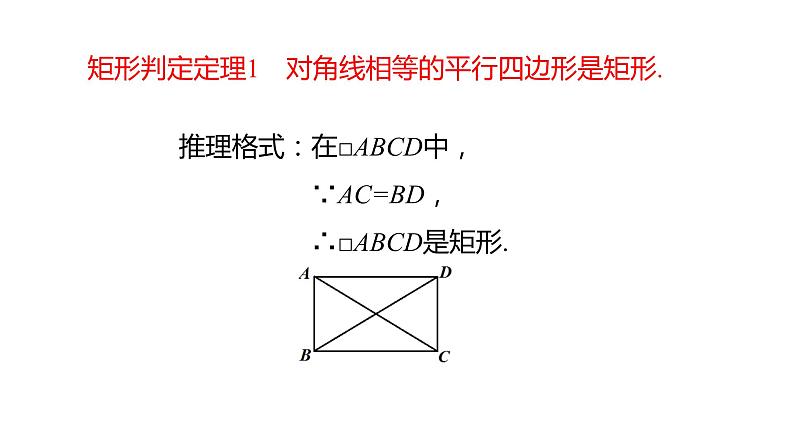
矩形判定定理1 对角线相等的平行四边形是矩形.
已知：□ ABCD中，AC=DB。
求证：□ ABCD是矩形
证明：在 □ ABCD中， AB=DC， AC=DB，BC=CB， ∴ △ABC≌△DCB(SSS) ∠ABC=∠DCB又∵ AB∥DC ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=0.5×180°=90° ∴ □ ABCD是矩形
矩形的四个角都是直角，反过来，一个四边形至少有几个角是直角时，这个四边形就是矩形呢？
因为四边形的内角和是360°，若有三个角是直角，则第四角也就是直角
矩形判定定理2：有三个角是直角的四边形是矩形.
3.矩形判定方法小结：（1）有一个角是直角的平行四边形是矩形；（2）对角线相等的平行四边形是矩形；（对角线相等又平分的四边形是矩形）（3）有三个角是直角的四边形是矩形.
下列各句判定矩形的说法是否正确？
（1）对角线相等的四边形是矩形；
（2）对角线互相平分且相等的四边形是矩形；
（3）有一个角是直角的四边形是矩形；
（5）有三个角是直角的四边形是矩形；
（6）四个角都相等的四边形是矩形；
（7）对角线相等，且有一个角是直角的四边形是矩形；
（10）一组邻边垂直，一组对边平行且相等的四边形是矩形；
（9）对角线相等且互相垂直的四边形是矩形；
（8）一组对角互补的平行四边形是矩形；
（4）有三个角都相等的四边形是矩形;
你有什么方法检查你家的门框是不是矩形？
如果仅有一根较长的绳子，你怎样检查？说明理由.
方法二：①先检查两组对边是否相等， 判断它是否是一个平行四边形； ②再检查对角线是否相等， 判断它是否是一个矩形.
方法一：检查三个角是不是直角
方法三：①对角线是不是互相平分，
例2 如图，在□ABCD中，对角线AC与BD相交于点O， △ABO是等边三角形，AB=4，求□ABCD的面积.
解：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD.
又∵△ABO是等边三角形，
∴OA=OB=AB=4.
∴OA=OC=OB=OD=4.
∴AC=BD=2OA=2×4=8.
在Rt△ABC中，由勾股定理，得AB2+BC2=AC2
练习： 如果平行四边形四个内角的平分线能够围成一个四边形，那么这个四边形是矩形．
已知：如图，□ABCD的四个内角的平分线分别相交于E、F、G、H，
求证：四边形 EFGH为矩形．
证明：∵AB∥CD　　∴∠ABC＋∠BCD=180°　　∵BG平分∠ABC，CG平分∠BCD       
∴∠BGC=90°同理可证∠AFB=∠AED=90°∴四边形EFGH是矩形．(有三个角是直角的四边形是矩形)
∴∠GBC＋∠BCG=0.5 ∠ABC＋0.5∠BCD=0.5(∠ABC＋∠BCD)=0.5×180°=90°
2．如图，在等边△ABC中，点D是BC边的中点，以AD为边作等边△ADE．（1）求∠CAE的度数；（2）取AB边的中点F，连结CF、CE，试证明四边形AFCE是矩形．
解析：（1）在等边△ABC中，∵点D是BC边的中点，∴∠DAC＝30º，又∵等边△ADE，∴∠DAE＝60º，∴∠CAE＝30º.
∴四边形AFCE是平行四边形，
（2）在等边△ABC中，∵F是AB边的中点，D是BC边的中点，
∴CF＝AD，∠CFA＝90º，
由（1）知∠CAE＝30º，
∴∠CFA＝∠EAF，∴CF∥AE，
∴四边形AFCE是矩形．
∴∠EAF＝60º+30º＝90º，
又∵∠CFA＝90º，
习题1.5 1，2，3，4
(2)若CE＝12，CF＝5，求OC的长；
(3)当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．
3.如图,在△ABC中，点O在AB边上,过点O作BC的平行线交∠ABC的平分线于点D,过点B作BE⟂BD交直线OD于点E.
(l)求证:OE=OD;
(2)当点O在AB的什么位置时，四边形BDAE是矩形?说明理由.
4.如图,在口ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF、BF.(1)求证:四边形BFDE是矩形;
4.如图,在口ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF、BF.
5.如图▢ABCD的对角线AC、BD相交于点0.E、F是AC上的两点,并且AE=CF，连接DE、BF.(1)求证:△DOE≌△BOF;
(2)若BD=EF，连接EB、DF,判断四边形EBFD的形状,并说明理由.
6.如图,在菱形ABCD中，对角线AC与BD相交于点0.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.(1)求证:四边形OCED是矩形;
9.在▢ABCD中，过点D作DE⊥AB于点E,点F在边CD上,DF= BE,连接AF,BF，(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4，DF=5,求证:AF平分∠DAB.
10.如图 ,在□ABCD中，DC >AD,四个角的平分线AE、DE、BF、CF的交点分别是E、F,过点E、F分别作DC与AB间的垂线MM'与NN',在DC与AB.上的垂足分别是M、N与M'、N',连接EF.(1 )求证:四边形EFNM是矩形;