人教版九年级上册第二十四章 圆综合与测试巩固练习

这是一份人教版九年级上册第二十四章 圆综合与测试巩固练习，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

班级________姓名________得分________


一、选择题（每题3分，共30分）


1．下列说法正确的是 ( )


A．相等的圆心角所对的孤相等 B．90°的角所对的弦是直径


C．等弧所对的弦相等 D．圆的切线垂直于半径


2．在⊙O中，AB是弦，圆心到AB的距离为1，若⊙O的半径为2，则弦AB的长为 ( )


A． B．2 C．D．2


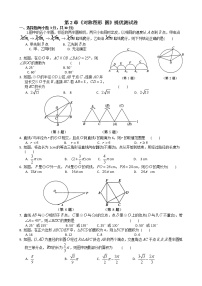
3．如图，已知PA切⊙O于A，⊙O的半径为3，OP＝5，则切线长PA为 ( )


A． B．8 C．4


4．设⊙O的半径为R，圆心到点A的距离为d，且R，d分别是方程x2－6x＋8＝0的两根，则点A与⊙O的位置关系是 ( )


A．点A在⊙O内部 B．点A在⊙O上C．最A在⊙O外部 D．点A不在⊙O上


5．如图，AB是⊙O的直径，C，D是⊙O上的两点，若∠ABC＝70°，则∠BDC的度数为 ( ) A．50° B．40° C．30° D．20°


6．已知正三角形的边长为a，其内切圆的半径为r，外接圆的半径为R，则r：a：R等于 ( )


A．1：2：2B．1：：2 C．1：2： D．1：：2


7．图中实线部分是半径为9m的两条等弧组成的游泳池，若每条弧所在的圆都经过另一个圆的圆心，则游泳池的周长为 ( )


A．12π m B．18π m C．20π m D．24π


8．如图，将半径为2的圆形纸片，沿半径OA，OB将其裁成1：3两个部分，用所得扇形围成圆锥的侧面，则圆锥的底面半径为 ( )


A． B．1C．1或3 D．或


9.已知矩形的边，，以点为圆心作圆，使，，三点至少有一点在内，且至少有一点在外，则的半径的取值范围是（）


10．如图，中，，，，是的外接圆，是优弧上任意一点（不包括，），记四边形的周长为，的长为，则关于的函数关系式是（）


A. B. C. D.


二、填空题（每题3分，共24分）


11．已知两直角边是5和12的直角三角形，则其内切圆的半径是_______．


12．已知弦AB的长等于⊙O的半径，则弦AB所对的圆周角是_______．


13．已知圆锥底面半径是2，母线长是4，则圆锥的侧面展开的扇形圆心角是_______．


14. 已知：内一点到圆的最大距离是，最小距离是，则这个圆的半径是________．





第16题 第17题 第18题


15．在△ABC中，∠A＝50°，若O为△ABC的外心，∠BOC＝_______；若I为△ABC的内心，∠BIC＝_______．


16．如图，OC是⊙O的半径，AB是弦，且OC⊥AB，点P在⊙O上，∠APC＝26°，则∠BOC＝_______．


17.如图，已知为的切线，的直径是，弦，则______度．


18.如图，过、、三点的圆的圆心为，过、、三点的圆的圆心为，如果，那么________．


三、解答题（共46分）


19.（8分）已知⊙O的直径AB的长为4 cm，C是⊙O上一点，∠BAC＝30°，过点C作⊙O的切线交AB的延长线于点P，求BP的长．





20.如图，已知直线交于、两点，是的直径，为的切线，为切点，且，垂足为．


若，求的度数；


若，的直径为，求的长度．

















21．26.如图，为的直径，是上一点，过点的直线交的延长线于点，，垂足为，是与的交点，平分．


求证：是的切线；若，，求图中阴影部分的面积．

















22.如图13所示，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D的切线分别交AB，AC的延长线于点E，F.


(1)求证：AF⊥EF；


(2)小强同学通过探究发现：AF＋CF＝AB，请你帮助小强同学证明这一结论．



































23.（12分）如图，已知AB是⊙O的直径，PB为⊙O的切线，B为切点，OP⊥弦BC于点D且交⊙O于点E．


(1)求证：∠OPB＝∠AEC；


(2)若点C为半圆ACB弧的三等分点，请你判断四边形AOEC为哪种特殊四边形？并说明理由．


























24.在等腰梯形中，，，且．以为直径作交于点，过


点作于点．建立如图所示的平面直角坐标系，已知、两点坐标分别为、．


求、两点的坐标；求证：为的切线；


将梯形绕点旋转到，直线上是否存在点，使以点为圆心，为半径的与直线相切？如果存在，请求出点坐标；如果不存在，请说明理由．
























































参考答案


1．C 2.D 3．C 4.D 5.D 6．A 7.D 8.D 9．B 10.D


11.2


12.45°或 135°


13.180°


14.0.2


15.100° 115°


16.52°


17.8

18.3


19.


20．2(cm)．


21．(1)60°.(2)略 (3)


22．(1)△OBC是直角三角形．(2)10． (3)OF＝


23．(1)略 (2)是菱形





24.解：连接，如图，


∵是的直径，


∴轴，


∵四边形为等腰梯形，


∵，


，





∴，


∴；





证明：连接，如图，在中，


∵，


∴，








在等腰梯形中，


∴


∴


又∵


∴


∴为的切线．存在．理由如下：


过作于，且交于


∵梯形与梯形关于点成中心对称


∴，


∴且，


在中，，，


∴


在中，


•，


∴．


设点存在，则，


作轴于点，


∴，


，


①若点在的延长线上，


∴，


∴．


②若点在的延长线上，


∴，


∴．


∴在直线上存在点和，使以点为圆心，为半径的与直线相切．


A.
B.
C.
D.