





数学八年级上册第3章 一元一次不等式3.2 不等式的基本性质示范课ppt课件
展开第3章 一元一次不等式3.2 不等式的基本性质
同学们,让我们一起乘坐幸福快车,领略一路的数学美景!
3.2 不等式的基本性质
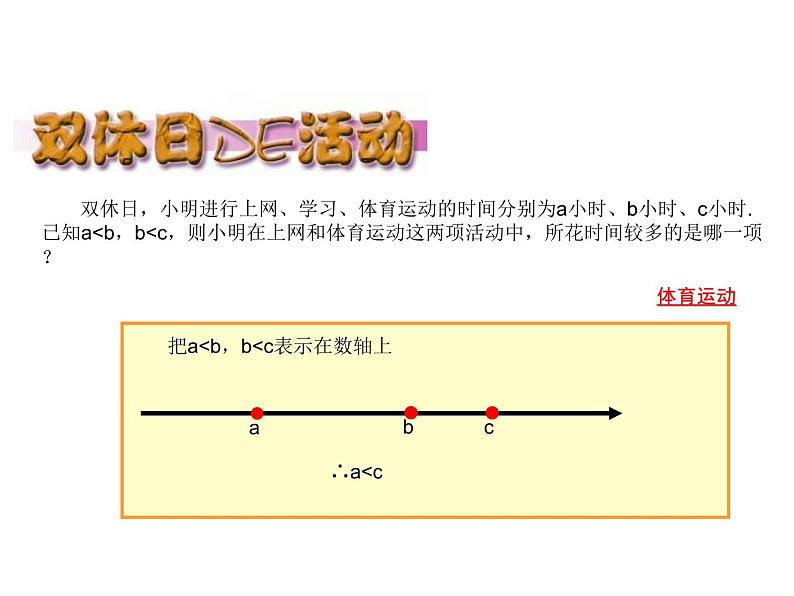
双休日,小明进行上网、学习、体育运动的时间分别为a小时、b小时、c小时. 已知a
判一判:1、若m>0,0>n,则m > n.( )2、若x >y,则y < x.( )3、若p<r, r<h, 则p<r<h.( )
双休日,小明、小慧分别进行1小时和0.5小时的体育运动. 由于运动会临近,他们需要对参加的体育项目进行训练,两人都增加了0.5小时的运动时间,请问增加运动时间之后,谁的运动时间长?
1+0.5 > 0.5+0.5
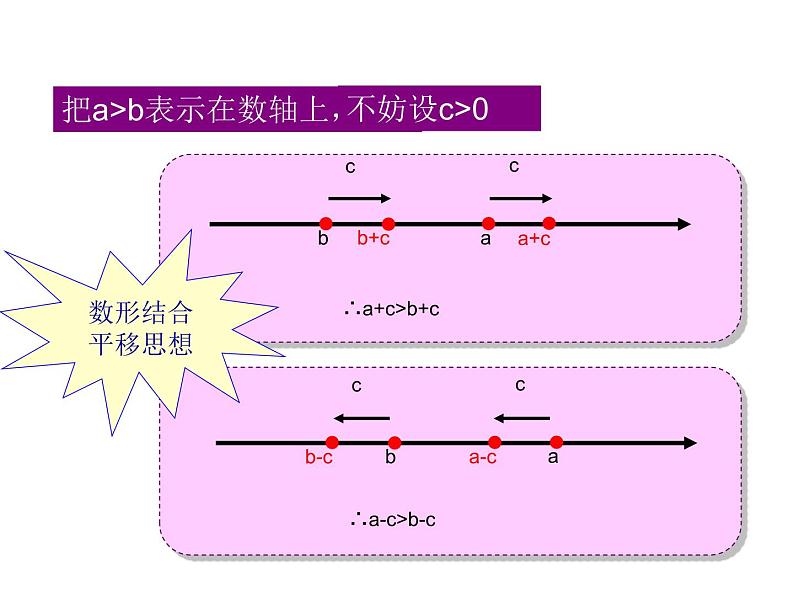
若a>b,则a+c__b+c; a-c__b-c.
把a>b表示在数轴上,
不等式的两边都加上(或都减去)同一个数,所得到的不等式仍成立.
如果a>b,那么a+c>b+c,a-c>b-c;如果a<b,那么a+c<b+c,a-c<b-c.
选择适当的不等号填空,并说明理由.
温馨提示: 在不等式的基本性质中,a、b、c代表的可以是数字、字母,还可以是多项式。
8__128×4__12×48÷4__12÷48×(-4)__12×(-4)8÷(-4)__12÷(-4)
想一想:从上面的变化,,你发现了什么?
如果a>b, 且c>0,那么ac>bc, > ;如果a>b,且c<0,那么ac<bc, < ;
不等式的两边都乘(或都除以)同一个正数,所得的不等式仍成立;
不等式的两边都乘(或都除以)同一个负数,必须改变不等号的方向,所得的不等式成立.
如果a>b,且c>0,那么ac>bc, > ;如果a>b,且c<0,那么ac<bc, < ;
若a<b,b<c,则a<c
如果a>b,那么a+c>b+c,a-c>b-c
如果a=b,那么a+c=b+c,a-c=b-c
若a=b,b=c,则a=c
等式与不等式的基本性质的区别与联系
设a=-1,则 2a=-2. ∵-2<-1, ∴2a <a.
例1 已知a<0 ,试比较2a与a的大小.
∵2a-a=a <0,∴2a<a.
如图,在数轴上分别表示2a和a的点(a<0).2a位于a的左边,所以2a<a.
利用不等式基本性质2:
∵a<0,∴ a+a<0+a,即2a <a.
∵2>1,a<0,∴2a<a.
试比较2a与a的大小.
当a>0时, 当a=0时, 当a<0时,
若x>y,比较2-3x与2-3y的大小,并说明理由.
(不等式的基本性质3)
(不等式的基本性质2)
若x>y,且(a-3)x<(a-3)y,求a的取值范围.
解:∵x>y,且(a-3)x<(a-3)y,
∴a-3<0(不等式的基本性质3)
∴a<3(不等式的基本性质2)
若x>y,请比较(a-3)x与(a-3)y的大小.
比较等式与不等式的基本性质. 例如, 等式是否有与不等式的基本性质1类似的传递性?不等式是否有与等式的基本性质类似的移项法则?你可以用列表的方式进行对比.
若a=b,b=c,则a=c
若a<b, b<c, 则a<c
如果a=b,那么a+c=b+c,a-c=b-c
比较等式与不等式的基本性质
小明和小华在探究数学问题.小明说: “ 3y>4y ”.小华认为小明说错了,应该是3y<4y,聪明的你觉得呢?
解:当y>0时, 3y < 4y;
当y < 0时, 3y >4y.
当y= 0时, 3y = 4y;
初中数学第3章 一元一次不等式3.2 不等式的基本性质教学演示课件ppt: 这是一份初中数学第3章 一元一次不等式3.2 不等式的基本性质教学演示课件ppt,共26页。PPT课件主要包含了教学目标,x>-1,x<-2,-1<x<2,观察1,2b与c,3a与c,你能得出什么结论,不等式的基本性质1,观察2等内容,欢迎下载使用。
初中数学3.2 不等式的基本性质课文配套ppt课件: 这是一份初中数学3.2 不等式的基本性质课文配套ppt课件,共18页。PPT课件主要包含了猜一猜,算一算,说一说,画一画,试一试,例已知a0,我学会了什么等内容,欢迎下载使用。
数学八年级上册3.2 不等式的基本性质图片课件ppt: 这是一份数学八年级上册3.2 不等式的基本性质图片课件ppt,共15页。PPT课件主要包含了若ab则,acbc,数形结合,猜想1,∴a-cb-c,∴a+cb+c,猜想2,分类讨论,填一填,猜想3等内容,欢迎下载使用。














