浙教版九年级上册第1章 二次函数1.3 二次函数的性质课文配套ppt课件

这是一份浙教版九年级上册第1章 二次函数1.3 二次函数的性质课文配套ppt课件，共25页。PPT课件主要包含了１顶点坐标与对称轴，２位置与开口方向，３增减性与最值，抛物线，顶点坐标，对称轴，开口方向，增减性，根据图形填表，例题探究等内容，欢迎下载使用。

函数 y=ax2+bx+c基本性质回顾
二次函数y=ax2+bx+c（a≠0）的图像是一条抛物线，
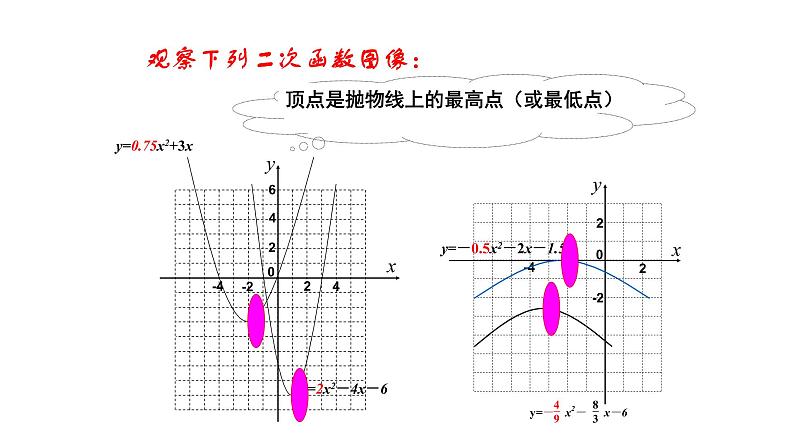
观察下列二次函数图像：
顶点在图像的位置有什么特点？
顶点是抛物线上的最高点（或最低点）
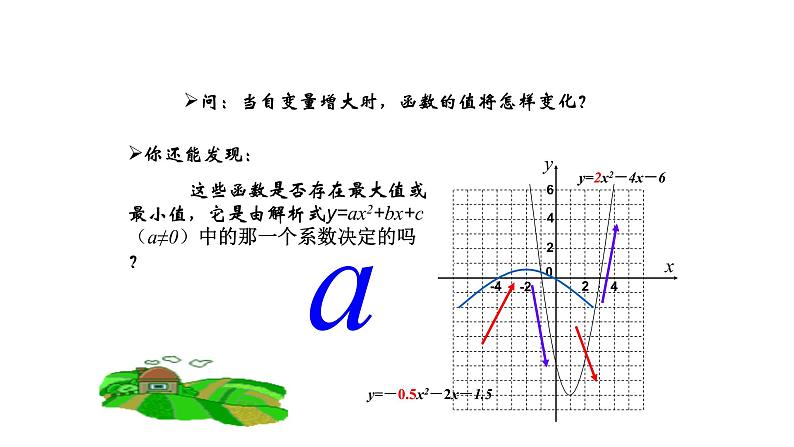
问：当自变量增大时，函数的值将怎样变化？
你还能发现： 这些函数是否存在最大值或最小值，它是由解析式y=ax2+bx+c（a≠0）中的那一个系数决定的吗？
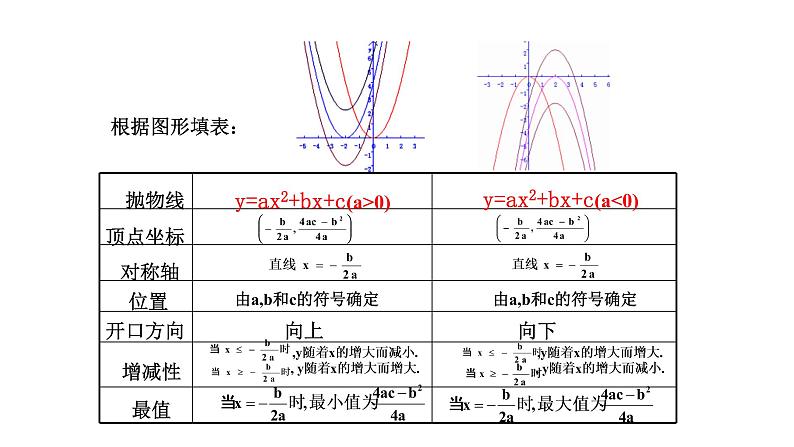
二次函数y=ax2+bx+c(a≠0)的图象和性质
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
,y随着x的增大而减小., y随着x的增大而增大.
,y随着x的增大而增大., y随着x的增大而减小.
解：（1）∵a=－0.5,b=－7,c=7.5;
所以函数y=－0.5x2－7x＋7.5的大致图像如图：
⑵自变量x在什么范围内时，y随x 的增大而增大？何时y 随x的增大而减小？并求出函数的最大值或最小值。
解： ⑵由右图可知，当x≤－7时， y随x 的增大而增大；
当x≥－7 时，y 随x的增大而减小；
当x＝－7时，函数有最大值32。
(3)求图象与坐标轴交点构成的三角形的面积?
（4）根据图象，说 出 x 取哪些值时， ① y=0; ② y<0; ③ y>0.
当x=-15或x=1时
当x＜-15或x ＞ 1时
已知函数y=x2－3x－4.⑴求函数图像的顶点坐标、与坐标轴交点的坐标和对称轴，并画出函数的大致图像；
解：∵ y=x2－3x－4 ＝(x－1.5)2－6.25,∴图象顶点坐标为(1.5, －6.25);
又当y=0时，得x2－3x－4＝0的解为： x1＝－1，x2＝4。则与x轴的交点为(－1,0)和(4,0)
与y轴的交点为(0, －4)
⑵如右图可知: y2＞ y1 ＞ y3
2、二次函数y=x2＋bx+9的图象顶点在X轴上，那么b等于多少？
如果二次函数y=ax2+bx+c (a≠0)的图像与x轴的两个交点的 坐标为 （ x1，0 ）和（ x2 ，0）
方程ax2+bx+c＝0 (a≠0)的解与二次函数y=ax2+bx+c (a≠0)的图像与x轴交点的坐标有什么关系？
那么x1和 x2 恰好是方程ax2+bx+c＝0 (a≠0)的两个根
方程ax2+bx+c＝0 (a≠0)的解就是 函数y=ax2+bx+c (a≠0)的图像与x轴交点的 坐标。
可以发现：二次函数y=ax2+bx+c (a≠0)的图像与x轴交点的 存在性与
方程ax2+bx+c＝0 (a≠0)的
那么，进一步推想方程ax2+bx+c＝0 (a≠0)解的存在性又与什么有关呢？
b2 －4ac的正负性有关。
故而：①当b2 －4ac 时，抛物线与x轴有 交点；
②当b2 －4ac 时，抛物线与x轴只有 交点；
③当b2 －4ac 时，抛物线与x轴 交点。
＞0 两个
＝0 一个
＜0 没有
⑴ y=2X２-X-1 ⑵ y=4X2+4X+1 ⑶ y=3X2+2X+5
1、抛物线与x轴的交点的个数：
2、抛物线y=x2-5x+4与坐标轴的交点个数为（ ）（A）0个 （B）1个 （C）2个 （D）3个
二次函数y=ax2+bx+c(a≠0)的图象如图所示，则a__0，b__0，c__0　
2、已知二次函数的图像如图所示，下列结论：⑴a+b+c﹤0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a其中正确的结论的个数是（ ）A 1个 B 2个 C 3个 D 4个
1、抛物线y=ax2+bx (a≠0)的顶点在第二象限，则a__0，b__0.　
2、二次函数y=ax2+bx ，当a＞0，b＜0时，它的图象经过____________象限。　
已知抛物线y=x2-2x +m的函数值恒大于零，求m的取值范围.　
大家应该很好的利用二次函数图像给我们的启迪，来解决诸多问题！
已知某抛物线的对称轴是直线x=1，该抛物线上最低点的纵坐标是 -1，且抛物线经过（0，1），求该抛物线的解析式.
⑴球运动路线的函数解析式和自变量的取值范围；
⑵球在运动中离地面的最大高度。
篮球运动员投篮时，球运动的路线为抛物线的一部分（如图），抛物线的对称轴为x=2.5。求：
则：a=－0.2,k=3.5
解: ⑴设函数解析式为:y=a(x－2.5)2+k,根据题意，得：
∴解析式为:y=－0.2x2+x+2.25,自变量x的取值范围为：0≤x≤4.
⑵球在运动中离地面的最大高度 为3.5米。
一运动员推铅球，铅球经过的路线为如图所示的抛物线。 （1）求铅球所经过的路线的函数解析式和自变量取值范围。 （2）铅球的落地点离运动员有多远？