初中数学第1章 二次函数1.3 二次函数的性质习题课件ppt

这是一份初中数学第1章 二次函数1.3 二次函数的性质习题课件ppt，共31页。PPT课件主要包含了答案显示，见习题，答案C，答案A，答案D等内容，欢迎下载使用。

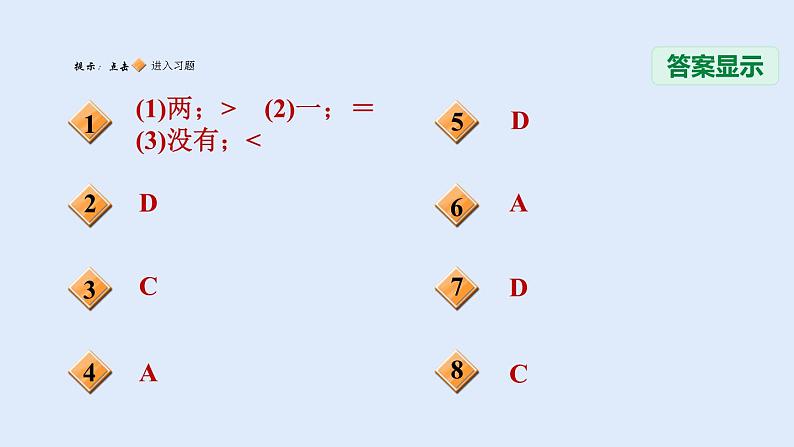
(1)两；>　(2)一；＝　(3)没有；<
(1)－3.(2)(2，－5)或(－2，－5)．
(1)c＜2.(2)m＜n.理由略.
1．观察图象(如图)填空：(1)二次函数y＝x2＋x－2的图象与x轴有________个交点，则一元二次方程x2＋x－2＝0的根的判别式b2－4ac________0；(2)二次函数y＝x2－6x＋9的图象与x轴有________个交点，则一元二次方程x2－6x＋9＝0的根的判别式b2－4ac________0；(3)二次函数y＝x2－x＋1的图象与x轴________公共点，则一元二次方程x2－x＋1＝0的根的判别式b2－4ac________0.
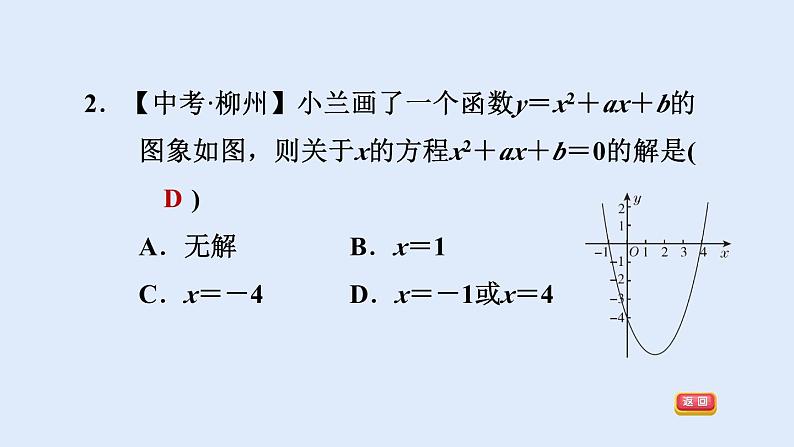
2．【中考·柳州】小兰画了一个函数y＝x2＋ax＋b的图象如图，则关于x的方程x2＋ax＋b＝0的解是(　　)A．无解 B．x＝1C．x＝－4 D．x＝－1或x＝4
3．【中考·宿迁】若二次函数y＝ax2－2ax＋c的图象经过点(－1，0)，则关于x的方程ax2－2ax＋c＝0的解为(　　)A．x1＝－3，x2＝－1 B．x1＝1，x2＝3C．x1＝－1，x2＝3 D．x1＝－3，x2＝1
【点拨】∵二次函数y＝ax2－2ax＋c的图象经过点(－1，0)，∴方程ax2－2ax＋c＝0一定有一个解为x＝－1.∵抛物线的对称轴为直线x＝1，∴二次函数y＝ax2－2ax＋c的图象与x轴的另一个交点为(3，0)．∴方程ax2－2ax＋c＝0的解为x1＝－1，x2＝3.
5．下列抛物线中，与x轴有两个交点的是(　　)A．y＝3x2－5x＋3 B．y＝4x2－12x＋9C．y＝x2－2x＋3 D．y＝2x2＋3x－4
6．【中考·永州】抛物线y＝x2＋2x＋m－1与x轴有两个不同的交点，则m的取值范围是(　　)A．m<2 B．m>2 C．08．【中考·杭州】在平面直角坐标系中，已知a≠b，设函数y＝(x＋a)(x＋b)的图象与x轴有M个交点，函数y＝(ax＋1)(bx＋1)的图象与x轴有N个交点，则(　　)A．M＝N－1或M＝N＋1 B．M＝N－1或M＝N＋2C．M＝N或M＝N＋1 D．M＝N或M＝N－1
【点拨】∵y＝(x＋a)(x＋b)＝x2＋(a＋b)x＋ab，a≠b，∴(a＋b)2－4ab＝(a－b)2＞0.∴函数y＝(x＋a)(x＋b)的图象与x轴有2个交点，即M＝2.∵函数y＝(ax＋1)(bx＋1)＝abx2＋(a＋b)x＋1，∴当ab≠0时，(a＋b)2－4ab＝(a－b)2＞0，此时函数y＝(ax＋1)(bx＋1)的图象与x轴有2个交点，即N＝2，则M＝N；当ab＝0时，不妨令a＝0，∵a≠b，∴b≠0，此时函数y＝(ax＋1)(bx＋1)＝bx＋1为一次函数，其图象与x轴有1个交点，即N＝1，则M＝N＋1.综上可知，M＝N或M＝N＋1.
10．【中考·荆门】抛物线y＝－x2＋4x－4与坐标轴的交点个数为(　　)A．0 B．1 C．2 D．3
【点拨】此题容易遗漏与y轴的交点而错选B.
11．【中考·湖州】已知抛物线y＝2x2－4x＋c与x轴有两个不同的交点．(1)求c的取值范围； 
解：∵抛物线y＝2x2－4x＋c与x轴有两个不同的交点，∴16－8c＞0，解得c＜2.
(2)若抛物线y＝2x2－4x＋c经过点A(2，m)和点B(3，n)，试比较m与n的大小，并说明理由． 
解：m＜n.理由如下：∵抛物线y＝2x2－4x＋c的对称轴为直线x＝1，∴点A(2，m)和点B(3，n)都在对称轴的右侧．∵当x≥1时，y随x的增大而增大，∴m＜n.
12．【中考·云南】已知k是常数，抛物线y＝x2＋(k2＋k－6)x＋3k的对称轴是y轴，并且与x轴有两个交点．(1)求k的值； 
解：∵抛物线y＝x2＋(k2＋k－6)x＋3k的对称轴是y轴，∴k2＋k－6＝0，解得k1＝－3，k2＝2.又∵抛物线y＝x2＋(k2＋k－6)x＋3k与x轴有两个交点，∴0－4×1×3k＝－12k＞0，即k＜0.∴k＝－3.
(2)若点P在抛物线y＝x2＋(k2＋k－6)x＋3k上，且P到y轴的距离是2，求点P的坐标． 
解：由(1)得抛物线y＝x2－9.∵点P在抛物线y＝x2－9上，且P到y轴的距离是2，∴点P的横坐标为2或－2.当x＝2时，y＝－5；当x＝－2时，y＝－5，∴点P的坐标为(2，－5)或(－2，－5)．
13．【中考·丹东】某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系部分数据如下：
(1)已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式(不写出自变量x的取值范围)．
(2)如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？
解：根据题意，得(－2x＋100)(x－30)＝150，解这个方程，得x1＝35，x2＝45.故每件商品的销售价定为35元或45元时，每天获得150元利润．
(3)设该商店每天销售这种商品所获利润为w(元)，求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大．
解：根据题意，得w＝(－2x＋100)(x－30)＝－2x2＋160x－3 000＝－2(x－40)2＋200，∵a＝－2＜0，∴抛物线开口向下，函数有最大值，即当x＝40时，w的值最大，∴每件商品销售价定为40元时利润最大．
(2)当线段DE的长度最大时，求点D的坐标．