初中数学人教版八年级上册第十三章 轴对称综合与测试单元测试复习练习题

这是一份初中数学人教版八年级上册第十三章 轴对称综合与测试单元测试复习练习题，共9页。试卷主要包含了已知等内容，欢迎下载使用。
一．选择题


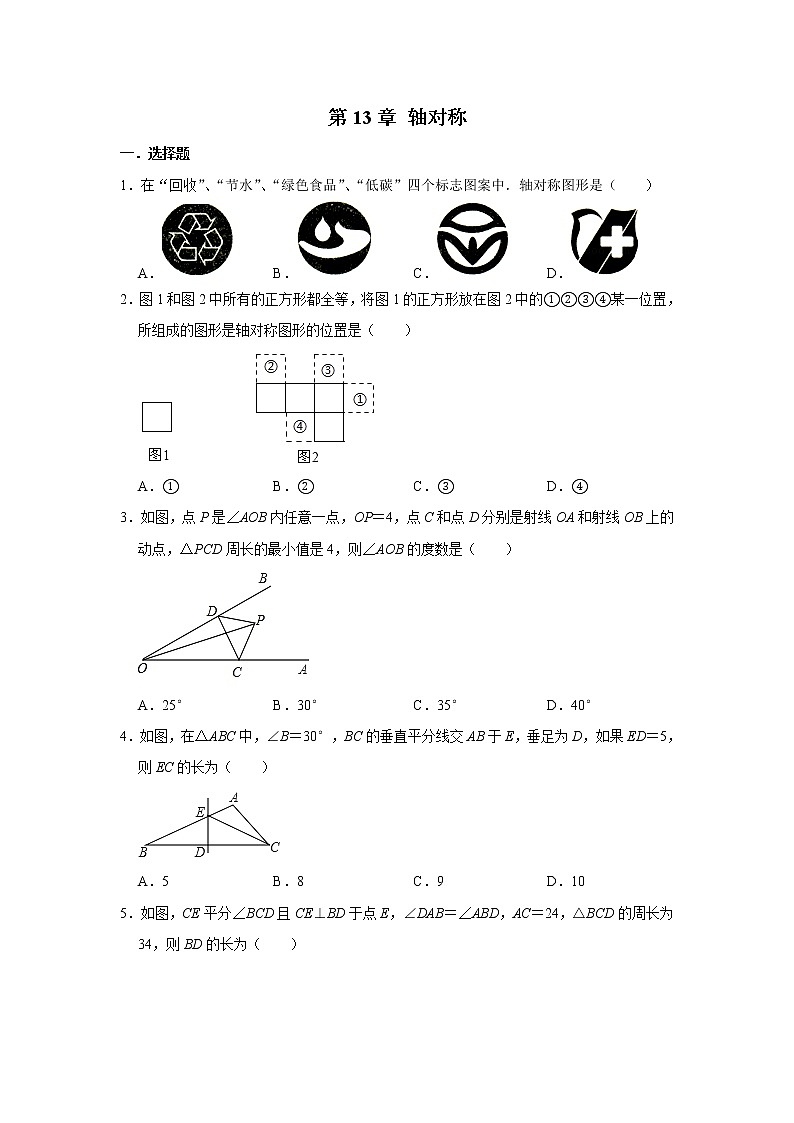
1．在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中．轴对称图形是（ ）


A．B．C．D．


2．图1和图2中所有的正方形都全等，将图1的正方形放在图2中的①②③④某一位置，所组成的图形是轴对称图形的位置是（ ）





A．①B．②C．③D．④


3．如图，点P是∠AOB内任意一点，OP＝4，点C和点D分别是射线OA和射线OB上的动点，△PCD周长的最小值是4，则∠AOB的度数是（ ）





A．25°B．30°C．35°D．40°


4．如图，在△ABC中，∠B＝30°，BC的垂直平分线交AB于E，垂足为D，如果ED＝5，则EC的长为（ ）





A．5B．8C．9D．10


5．如图，CE平分∠BCD且CE⊥BD于点E，∠DAB＝∠ABD，AC＝24，△BCD的周长为34，则BD的长为（ ）





A．10B．12C．14D．16


6．在日常生活中，你会注意到有一些含有特殊数学规律的车牌号码，如：浙C 80808、浙C 22222、浙C 12321等，这些牌照中的五个数字都是关于中间的一个数字“对称”的，我们不妨把这样的牌照叫做“数字对称”牌照．如果让你负责制作只以8和9为字母“C”后的第一个数字且有五个数字的“数字对称”牌照，那么最多可制作（ ）


A．2000个B．1000个C．200个D．100个


7．如图，在△ABC中，∠B＝30°，BC的垂直平分线交AB于E，垂足为D．如果CE＝10，则ED的长为（ ）





A．3B．4C．5D．6


8．如图所示，在△ABC中，∠C＝90°，DE垂直平分AB，交BC于点E，垂足为点D，BE＝6cm，∠B＝15°，则AC等于（ ）





A．6cmB．5cmC．4cmD．3cm


9．点（1，2）关于直线y＝x的对称点的坐标为（ ）


A．（2，1）B．（﹣2，1）C．（﹣1，2）D．（﹣1，﹣2）


10．已知：在△ABC中，∠A＝60°，如要判定△ABC是等边三角形，还需添加一个条件．现有下面三种说法：


①如果添加条件“AB＝AC”，那么△ABC是等边三角形；


②如果添加条件“∠B＝∠C”，那么△ABC是等边三角形；


③如果添加条件“边AB、BC上的高相等”，那么△ABC是等边三角形．


上述说法中，正确的有（ ）


A．3个B．2个C．1个D．0个


二．填空题


11．小刚从镜子中看到的电子表的读数是[15：01]，则电子表的实际度数是 ．


12．如图，已知△ABC中，AC＝BC，且点D在△ABC外，且点D在AC的垂直平分线上，连接BD，若∠DBC＝30°，∠ACD＝13°，则∠A＝ 度．





13．如图：已知在Rt△ABC中，∠C＝90°，∠A＝30°，在直线AC上找点P，使△ABP是等腰三角形，则∠APB的度数为 ．





14．等边△ABC，AB＝8，点D在直线AB上，若CD＝13，则AD的长为 ．


15．如图，等腰△ABC的底边BC长为4，面积是14，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为 ．





三．解答题


16．如图，△ABC中，∠BAC＝120°，BC＝20，AB的垂直平分线交BC于点D，垂足为点F，AC的垂直平分交BC于点E，垂足为点G．求：


（1）△ADE的周长，


（2）∠DAE的度数．





17．在△ABC中，AD平分∠BAC，BD＝CD，DE⊥AB于点E，DF⊥AC于点F，求证：AB＝AC．





18．如图，在△ABC中，AB＝AC，AB的垂直平分线MN交AC于点D，交AB于点E．


（1）求证：△ABD是等腰三角形；


（2）若∠A＝40°，求∠DBC的度数；


（3）若AE＝6，△CBD的周长为20，求△ABC的周长．





19．如图，在等边△ABC中，点D在BC边上，点E在AC的延长线上，DE＝DA．


（1）求证：∠BAD＝∠EDC；


（2）作出点E关于直线BC的对称点M，连接DM、AM，猜想DM与AM的数量关系，并说明理由．





20．如图，在△ABC中，AB＝AC，AB的垂直平分线MN交AC于点D，交AB于点E．


（1）若∠A＝40°，求∠DBC的度数；


（2）若AE＝6，△CBD的周长为20，求△ABC的周长．





21．如图，△ABC、△ADE是等边三角形，B、C、D在同一直线上．


求证：（1）CE＝AC+DC；（2）∠ECD＝60°．








参考答案


一．选择题


1． C．


2． C．


3． B．


4． D．


5． C．


6． C．


7． C．


8． D．


9． A．


10． A．


二．填空题


11． 10：21．


12． 73．


13． 15°、30°、75°、120°．


14． 7或15．


15．9．


三．解答题


16．解：（1）∵DE是线段AB的垂直平分线，


∴DA＝DB，


同理，EA＝EC，


∴△ADE的周长＝AD+DE+EA＝BD+DE+EC＝BC＝20；


（2）∵∠BAC＝120°，


∴∠B+∠C＝60°，


∵DA＝DB，EA＝EC，


∴∠DAB＝∠B，∠EAC＝∠C，


∴∠DAB+∠EAC＝60°，


∴∠DAE＝120°﹣60°＝60°．


17．解：∵AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，


根据角平分线上的点到角两边的距离相等得出DE＝DF，


又∵BD＝CD，∠DEB＝∠DFC＝90°，


∴Rt△DEB≌Rt△DFC，


∴∠B＝∠C，


∴AB＝AC．


18．证明：（1）∵AB的垂直平分线MN交AC于点D，


∴DB＝DA，


∴△ABD是等腰三角形；


（2）∵△ABD是等腰三角形，∠A＝40°，


∴∠ABD＝∠A＝40°，∠ABC＝∠C＝（180°﹣40°）÷2＝70°


∴∠DBC＝∠ABC﹣∠ABD＝70°﹣40°＝30°；


（3）∵AB的垂直平分线MN交AC于点D，AE＝6，


∴AB＝2AE＝12，


∵△CBD的周长为20，


∴AC+BC＝20，


∴△ABC的周长＝AB+AC+BC＝12+20＝32．


19．解：（1）如图1，∵△ABC是等边三角形，


∴∠BAC＝∠ACB＝60°．


又∵∠BAD+∠DAC＝∠BAC，∠EDC+∠DEC＝∠ACB，


∴∠BAD+∠DAC＝∠EDC+∠DEC．


∵DE＝DA，


∴∠DAC＝∠DEC，


∴∠BAD＝∠EDC．





（2）猜想：DM＝AM．理由如下：


∵点M、E关于直线BC对称，


∴∠MDC＝∠EDC，DE＝DM．


又由（1）知∠BAD＝∠EDC，


∴∠MDC＝∠BAD．


∵∠ADC＝∠BAD+∠B，


即∠ADM+∠MDC＝∠BAD+∠B，


∴∠ADM＝∠B＝60°．


又∵DA＝DE＝DM，


∴△ADM是等边三角形，


∴DM＝AM．





20．解：（1）解：∵在△ABC中，AB＝AC，∠A＝40°，


∴∠ABC＝∠C＝70°，


∵AB的垂直平分线MN交AC于点D，


∴AD＝BD，


∴∠ABD＝∠A＝40°，


∴∠DBC＝∠ABC﹣∠ABD＝30°．





（2）∵MN垂直平分AB，


∴DA＝DB，


∵BC+BD+DC＝20，


∴AD+DC+BC＝20，


∴AC+BC＝20，


∵AB＝2AE＝12，


∴△ABC的周长＝AB+AC+BC＝12+20＝32．





21．证明：（1）∵△ABC、△ADE是等边三角形，


∴AE＝AD，BC＝AC＝AB，∠BAC＝∠DAE＝60°，


∴∠BAC+∠CAD＝∠DAE+∠CAD，


即：∠BAD＝∠CAE，


∴△BAD≌△CAE，


∴BD＝EC，


∵BD＝BC+CD＝AC+CD，


∴CE＝BD＝AC+CD；





（2）由（1）知：△BAD≌△CAE，


∴∠ACE＝∠ABD＝60°，


∴∠ECD＝180°﹣∠ACB﹣∠ACE＝60°，


∴∠ECD＝60°．