北师大版 (2019)必修 第一册第五章 函数应用本章综合与测试单元测试练习题

这是一份北师大版 (2019)必修 第一册第五章 函数应用本章综合与测试单元测试练习题，共6页。试卷主要包含了函数的综合应用等内容，欢迎下载使用。

微专题集训五 函数的综合应用


专题1 增长函数模型差异比较的应用


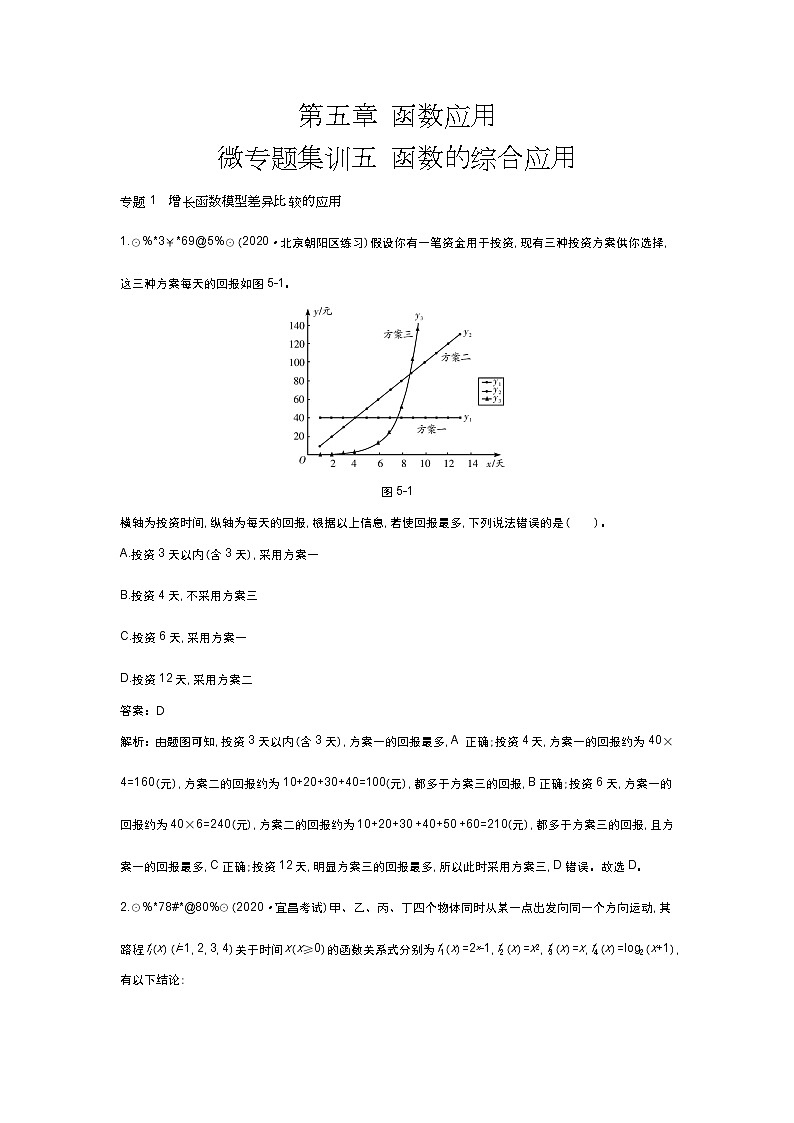
1.☉%*3￥*69@5%☉(2020·北京朝阳区练习)假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案每天的回报如图5-1。





图5-1


横轴为投资时间,纵轴为每天的回报,根据以上信息,若使回报最多,下列说法错误的是( )。


A.投资3天以内(含3天),采用方案一


B.投资4天,不采用方案三


C.投资6天,采用方案一


D.投资12天,采用方案二


答案：D


解析：由题图可知,投资3天以内(含3天),方案一的回报最多,A 正确;投资4天,方案一的回报约为40×4=160(元),方案二的回报约为10+20+30+40=100(元),都多于方案三的回报,B正确;投资6天,方案一的回报约为40×6=240(元),方案二的回报约为10+20+30 +40+50 +60=210(元),都多于方案三的回报,且方案一的回报最多,C正确;投资12天,明显方案三的回报最多,所以此时采用方案三,D错误。故选D。


2.☉%*78#*@80%☉(2020·宜昌考试)甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,f2(x)=x2,f3(x)=x,f4(x)=lg2(x+1),有以下结论:


①当x>1时,甲在最前面;②当x>1时,乙在最前面;③当01时,丁在最后面;④丙不可能在最前面,也不可能在最后面;⑤如果它们一直运动下去那么最终在最前面的是甲。


其中,正确结论的序号为 。


答案：③④⑤


解析：路程 fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,f2(x)=x2,f3(x)=x,f4(x)=lg2(x +1),它们相应的函数模型分别是指数型函数、二次函数、一次函数和对数型函数。


当x=2时,f1(2)=3,f2(2)=4,故①不正确。


当x=5时,f1(5)=31,f2(5)=25,故②不正确。


根据四种函数的变化特点,对数型函数的增长速度是先快后慢,当x=1时,甲、乙、丙、丁四个物体的路程相等,当01时,丁在最后面,故③正确。


结合对数型函数和指数型函数的图像变化情况,可知丙不可能在最前面,也不可能在最后面,故④正确。


指数型函数的增长速度是先慢后快,当运动的时间足够长,最前面的物体一定是按照指数型函数运动的物体,即一定是甲,故⑤正确。


3.☉%2￥5#4￥9￥%☉(2020·北京丰台区一模)某学校为了实现60万元的生源利润目标,准备制订一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且奖金y(单位:万元)随生源利润x(单位:万元)的增加而增加,但奖金总数不超过3万元,同时奖金不超过利润的20%。现有三个奖励模型:y=0.2x,y=lg5x,y=1.02x,其中哪个模型符合该校的要求?


答案：解:一次函数直线上升,指数函数爆炸增长,都会很快超过3万元,只有对数函数增长速度缓慢,满足题意。故只有模型y=lg5x符合该校的要求。


专题2 已知函数模型解决实际问题


4.☉%￥#0*￥269%☉(2020·宁波期末)某产品的总成本y(单位:万元)与产量x(单位:台)之间的函数关系式是y=3 000+20x-0.1x2(0

A.100台 B.120台 C.150台 D.180台


答案：C


解析：由题意,知3 000+20x-0.1x2≤25x,0

即x2+50x-30 000≥0,0

解得150≤x<240,且x∈N。


所以生产者不亏本时的最低产量是150台。故选C。


5.☉%*9*1￥￥80%☉(2020·雅安中学期中)某工厂8年来某种产品的总产量C与时间t(单位:年)的函数关系如图5-2。


以下四种说法:





图5-2


①前3年总产量增长速度越来越快;②前3年总产量增长速度越来越慢;③第3年后,这种产品停止生产;④第3年后产量保持不变。其中正确说法的序号是 。


答案：②③


解析： t∈[0,3]的图像反映了C随时间的变化而逐渐增长但增长速度越来越慢。由t∈(3,8]的图像,知总产量C没有变化,即第3年后停产,所以②③正确。


6.☉%69#*@8@3%☉(2020·天津七校联考)载人飞船是通过火箭发射的。已知某型号火箭的起飞重量M t是箭体(包括搭载的飞行器)的重量m t和燃料重量x t之和。在不考虑空气阻力的条件下,假设火箭的最大速度y km/s关于x的函数关系为y=k[ln(m+x)-ln(2m)]+4ln 2(k≠0)。当燃料重量为(e-1)m t时,该火箭的最大速度为4 km/s。


(1)求此型号火箭的最大速度y km/s与燃料重量x t之间的函数关系式;


答案：解:由题意,得4=k{ln[m+(e-1)m]-ln(2m)}+4ln 2,解得k=8,所以y=8[ln(m+x)-ln(2m)]+4ln 2=8lnm+xm。


(2)若此型号火箭的起飞重量是479.8 t,则应装载多少吨燃料(精确到0.1 t,取e≈2.718)才能使火箭的最大飞行速度达到8 km/s,顺利地把飞船发送到预定的椭圆轨道?


答案：由已知,得M=m+x=479.8,则m=479.8-x。


将y=8代入(1)中所得式中,得8=,解得x≈303.3。


所以应装载大约303.3 t燃料,才能使火箭的最大飞行速度达到8 km/s,顺利地把飞船发送到预定的椭圆轨道。


专题3 建立函数模型解决实际问题


7.☉%88*@93￥#%☉(2020·重庆市第一中学期中)某列火车从北京西站开往石家庄,全程277 km。火车出发10 min开出13 km,之后以120 km/h的速度匀速行驶。试写出火车行驶的总路程s与匀速行驶的时间t之间的函数关系式,并求离开北京2 h时火车行驶的路程。


答案：解:因为火车匀速行驶的总时间为(277-13)÷120=115(h),所以0≤t≤115。因为火车匀速行驶t h所行驶的路程为120t km,所以火车行驶的总路程s与匀速行驶的时间t之间的函数关系式为s=13+120t0≤t≤115。


离开北京2 h时火车匀速行驶的时间为2-16=116(h),此时火车行驶的路程s=13+120×116=233(km)。


8.☉%#30@61#￥%☉(2020·达州四模)某企业实行裁员增效,已知现有员工a人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的34,设该企业裁员x人后,年纯收益为y万元。


(1)写出y关于x的函数关系式,并指出x的取值范围;


答案：解:由题意,知y=(a-x)(1+0.01x)-0.4x=-1100x2+a100-140100x+a。


因为a-x≥34a,所以x≤14a。


故x的取值范围是0,a4上的自然数。


(2)当140

答案：因为y=-1100x-a2-702+1100a2-702+a,且140

当a为奇数时,x=a-12-70因为尽可能少裁员,所以舍去x=a+12-70,y取最大值。


所以当员工人数为偶数时,该企业裁员a2-70人才能获得最大的经济效益;


当员工人数为奇数时,该企业裁员a-12-70人才能获得最大的经济效益。


9.☉%6@6￥0@5*%☉(2020·保山统测试卷)某林区2013年木材蓄积量为200万m3,由于采取了封山育林、严禁砍伐等措施,木材蓄积量的年平均增长率达到5%。


(1)若经过x年后,该林区的木材蓄积量为y万m3,求y=f(x)的解析式,并求此函数的定义域;


答案：解:现有木材蓄积量为200万m3,


经过1年后木材蓄积量为200+200×5%=200(1+5%)万m3;


经过2年后木材蓄积量为200(1+5%)+200(1+5%)×5%=200(1+5%)2万m3;


……


经过x年后木材蓄积量为200(1+5%)x万m3,所以y=f(x)=200(1+5%)x(x∈N*)。


(2)作出函数y=f(x)的图像,并应用该图像求经过多少年后,林区的木材蓄积量能达到300万m3。


答案：作函数y=f(x)=200(1+5%)x(x≥0)的图像,如图。





作直线y=300,与函数y=200(1+5%)x的图像交于A点,则A点的坐标为(x0,300),A点的横坐标x0的值就是函数值y=300时,经过的时间x(年)的值。


经计算80
1
2
3
…
y
200
210
220.5
231.5
…