数学九年级上册21.2.1 配方法课文内容课件ppt

这是一份数学九年级上册21.2.1 配方法课文内容课件ppt，共21页。PPT课件主要包含了它们之间有什么关系，自主学习感受新知，总结归律，议一议，体现了转化的数学思想，配方得，移项得，开平方得，∴原方程的解为，当堂训练等内容，欢迎下载使用。

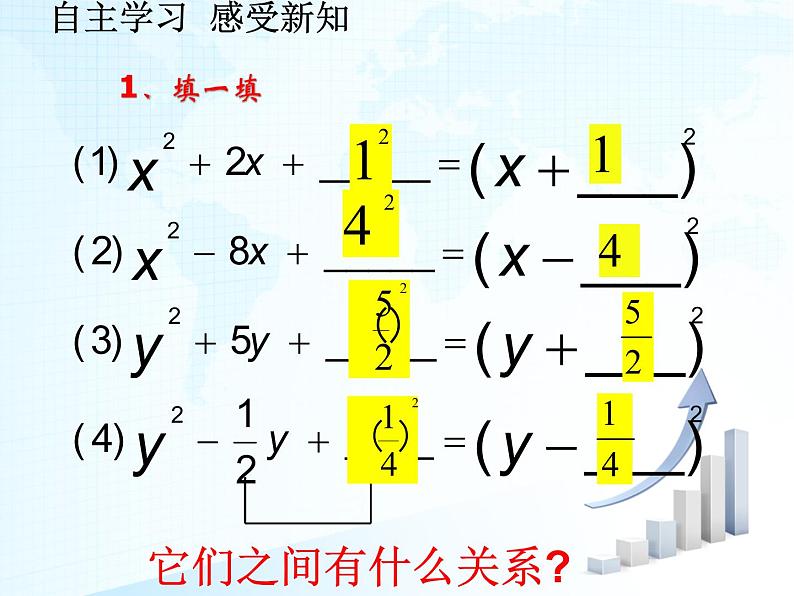
2、若4x2-mx+9是一个完全平方式，那么m的值是 。
对于x2+px,再添上一次项系数一半的平方,就能配出一个含未知数的一次式的完全平方式.
体现了从特殊到一般的数学思想方法
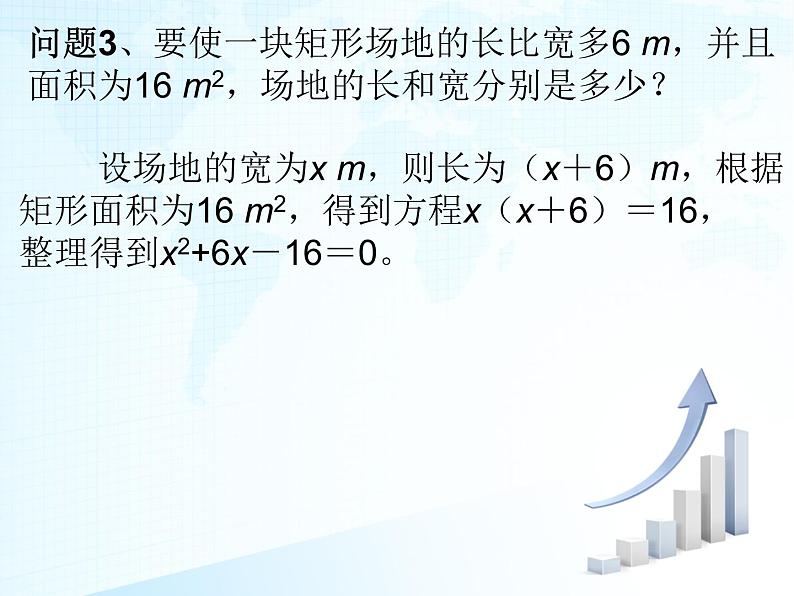
问题3、要使一块矩形场地的长比宽多6 m，并且面积为16 m2，场地的长和宽分别是多少？
设场地的宽为x m，则长为（x＋6）m，根据矩形面积为16 m2，得到方程x（x＋6）＝16，整理得到x2+6x－16＝0。
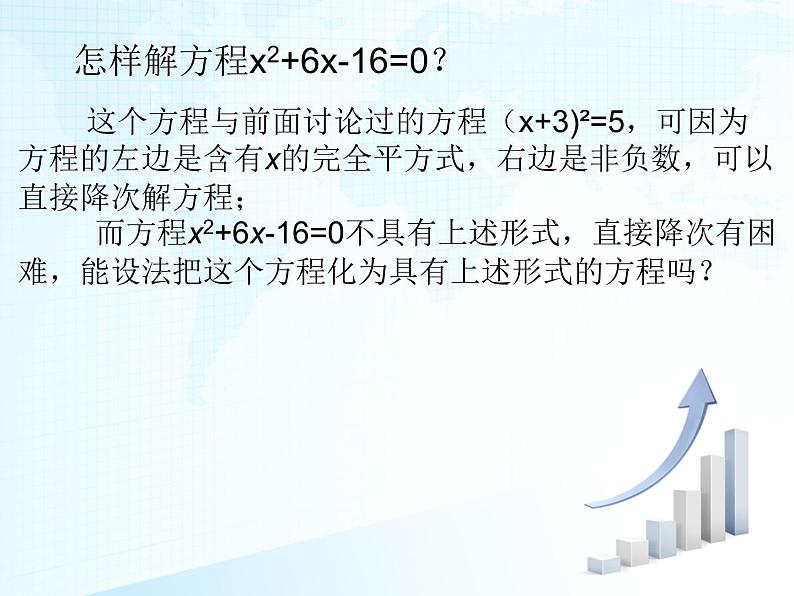
怎样解方程x2+6x-16=0？
这个方程与前面讨论过的方程（x+3)²=5，可因为方程的左边是含有x的完全平方式，右边是非负数，可以直接降次解方程； 而方程x2+6x-16=0不具有上述形式，直接降次有困难，能设法把这个方程化为具有上述形式的方程吗？
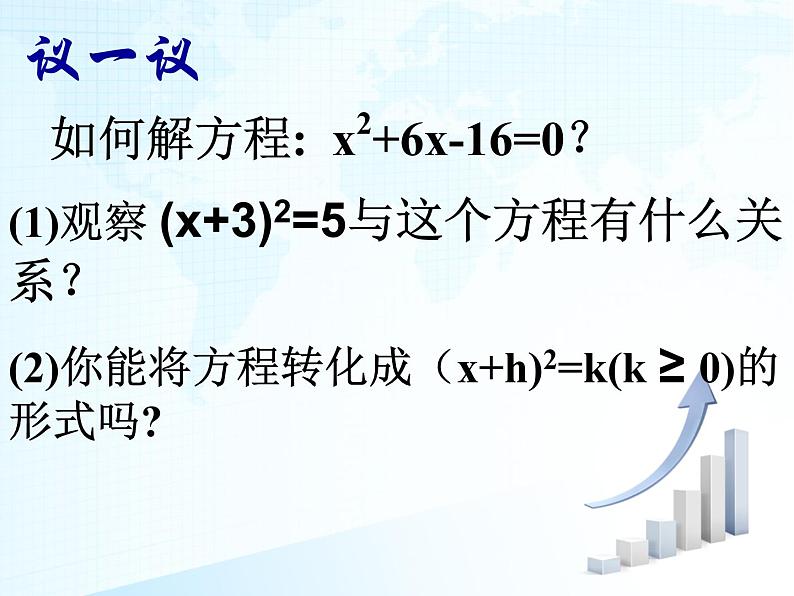
(1)观察 (x+3)2=5与这个方程有什么关系？(2)你能将方程转化成（x+h)2=k(k ≥ 0)的形式吗?
如何解方程: x2+6x-16=0？
变成了(x+h)2=k 的形式
通过配成完全平方式的形式解一元二次方程的方法，叫作配方法；配方的目的是为了降次，把一元二次方程转化为两个一元一次方程．
：配方时, 等式两边同时加上的是一次项系数一半的平方.

例1: 用配方法解方程
2、你能用配方法解方程吗？
二次项系数化为1，得：
二次项系数不为1，怎么办？
因为实数的平方不会是负数，所以x取任何实数时，（x-1)²都是非负数，所以上式不成立，即方程无实数根。
移项得：2x²-3x=-1
例2:用配方法解下列方程
用配方法解一元二次方程的步骤:
移项:把常数项移到方程的右边;配方:方程两边都加上一次项系数一 半的平方,将方程左边配成完全平方式开方:根据平方根意义,方程两边开平方;求解:解一元一次方程;定解:写出原方程的解.
1、用配方法解下列方程(1)x2＋10x+9=0(2)(3)3x²+6x=-4(4)4x²=3(2x+1)
(1)x2+4x-9=2x-11(2)x2-x=1(3)X(x+4)=8x+12
3.用配方法说明：不论k取何实数，多项式k2－3k＋5的值必定大于零.
练习1：用配方法解下列方程(1)
(2) x +x2 =9
(3)(x+1)2-10(x+1)+9=0
(4)x2+2mx=(n-m)(n+m)
1、配方法：像这样，把方程的左边配成含有x的完全平方形式，右边是非负数，从而可以用直接开平方法来解方程的方法就做配方法。2、用配方法解一元二次方程的步骤：①移项 ②化1 ③配方 ④降次 ⑤定解
小结：解一元二次方程的基本思路
把原方程变为(x+h)2＝k的形式(其中h、k是常数）。 当k≥0时，两边同时开平方，这样原方程就转化为两个一元一次方程。 当k<0时，原方程的解又如何？