人教版九年级上册24.4 弧长及扇形的面积教课ppt课件

这是一份人教版九年级上册24.4 弧长及扇形的面积教课ppt课件，共28页。PPT课件主要包含了知识回顾，学习目标，课堂导入，知识点1，新知探究，跟踪训练，知识点2，扇形面积公式，随堂练习，对接中考等内容，欢迎下载使用。

回忆小学学习的圆的知识，半径为 r 的圆，周长是多少？面积是多少？
2.会利用弧长和扇形面积的计算公式进行计算.
1.理解弧长和扇形面积公式的探求过程.
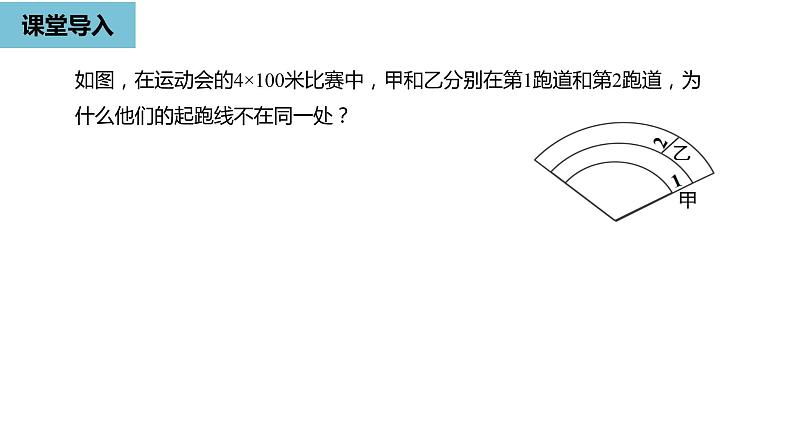
如图，在运动会的4×100米比赛中，甲和乙分别在第1跑道和第2跑道，为什么他们的起跑线不在同一处？
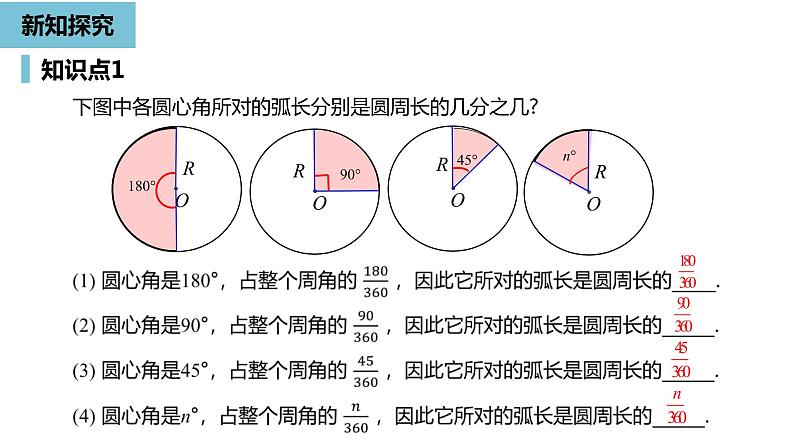
下图中各圆心角所对的弧长分别是圆周长的几分之几?
1.题目中若没有写明精确度，可用含 π 的代数式表示弧长，如弧长为 3π，11π 等. 2. 公式中的n和180表示倍数关系，没有单位.3.不要混淆弧长相等和弧相等，弧相等指两条弧全等，弧长相等指弧的长度相等.弧长相等的弧不一定是等弧，只有在同圆或等圆中，才是等弧.
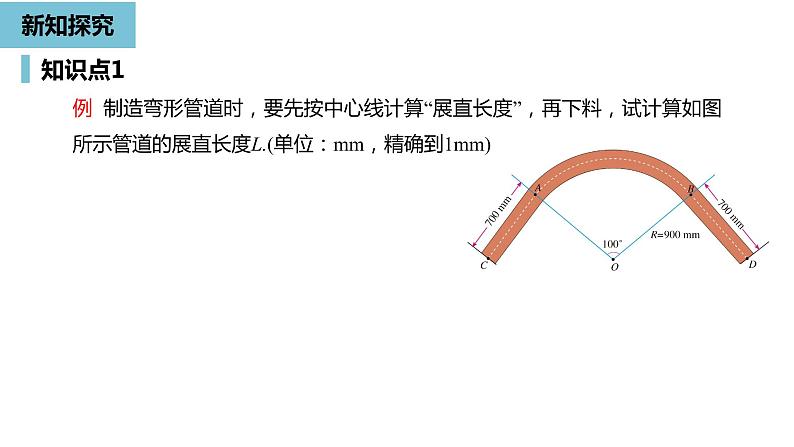
例 制造弯形管道时，要先按中心线计算“展直长度”，再下料，试计算如图所示管道的展直长度L.(单位：mm，精确到1mm)
已知扇形的圆心角为120°，弧长为10π cm，则该扇形的半径为 cm.
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.如图，劣弧AB与半径OA，OB围成的图形记作扇形OAB；优弧AB与半径OA，OB围成的图形记作扇形OACB.
下图中各扇形面积分别是圆面积的几分之几，具体是多少呢?
半径为r的圆中，圆心角为n°的扇形的面积
圆心角大小不变时，对应的扇形面积与半径有关，半径越长，面积越大.
圆的半径不变时，扇形面积与圆心角有关， 圆心角越大，面积越大.
扇形的面积与哪些因素有关？
扇形的弧长公式与面积公式有联系吗？
扇形的面积公式与什么公式类似？
(1) 截面上有水部分的面积是指图上哪一部分？
例 如图，水平放置的圆柱形排水管道的截面半径是0.6 m，其中水面高0.3m，求截面上有水部分的面积.（精确到0.01m）
(2) 水面高0.3 m是指哪一条线段的长？这条线段应该怎样画出来？
(3) 要求图中阴影部分的面积，应该怎么算？
由弦及弦所对的弧组成的图形叫做弓形.
(1) 已知扇形的半径为6 cm,面积为6π cm2，则该扇形的圆心角的度数为 .(2) （2018∙哈尔滨中考）一个扇形的圆心角为135° ，弧长为3π cm，则此扇形的面积是 cm2.
如图，实线部分是由两条等弧组成的游泳池，且这两条弧所在的圆的半径均为15 m.若每条弧所在的圆都经过另一个圆的圆心，则游泳池的周长是 m.
如图，AC是汽车挡风玻璃前的雨刷器，如果AO=45 cm， CO=5 cm，当AC绕点O顺时针旋转90°时，则雨刷器AC扫过的区城(阴影部分)的面积为 cm2(结果保留π).
在求解阴影部分面积的问题中，如果所求的阴影部分是不规则图形，可以采取各种方法，将阴影部分面积转化为几个规则图形面积的和或差的形式.与圆有关的阴影部分面积的问题，往往需要利用扇形面积公式或弓形面积的计算公式.
不规则图形面积的求解方法
如图，以BC为直径的⊙O与△ABC的另两边分别相交于点D,E.若∠A=60°,BC=4,则图中阴影部分的面积为______ (结果保留 π).
如图，矩形ABCD中，AB=4，BC=3，边CD在直线 l 上，将矩形ABCD沿直线 l 作无滑动翻滚，当点A第一次翻滚到点A1的位置时，则点A经过的路线长为 .
如图，AB为⊙O的直径，AC,DC为弦，∠ACD=60°，P为AB延长线上的点，∠APD=30°.(1) 求证：DP是⊙O的切线；(2) 若⊙O的半径为3，求图中阴影部分的面积.