人教版九年级上册第二十四章 圆24.4 弧长及扇形的面积教案配套课件ppt

这是一份人教版九年级上册第二十四章 圆24.4 弧长及扇形的面积教案配套课件ppt，共15页。PPT课件主要包含了课件说明，例题解析等内容，欢迎下载使用。

圆锥的侧面展开图是关于平面图形与空间几何体相互转换的教学内容，是培养学生空间想象能力和动手操作能力的重要内容．由于圆锥的侧面展开图是一个扇形，因此，利用弧长和扇形面积公式，可求得圆锥的侧面积，进而得出其全面积．学习计算圆锥侧面积和全面积，有助于培养学生的空间想象能力．
学习目标： 1．了解圆锥及其母线、侧面积、全面积等概念，会 　 计算圆锥的侧面积和全面积； 2．通过本节课的学习，学会观察、归纳的学习方法， 　 培养空间想象能力．学习重点： 圆锥的侧面积和全面积的计算．
　　你能利用手中的工具制作一个圆锥形的纸帽吗？
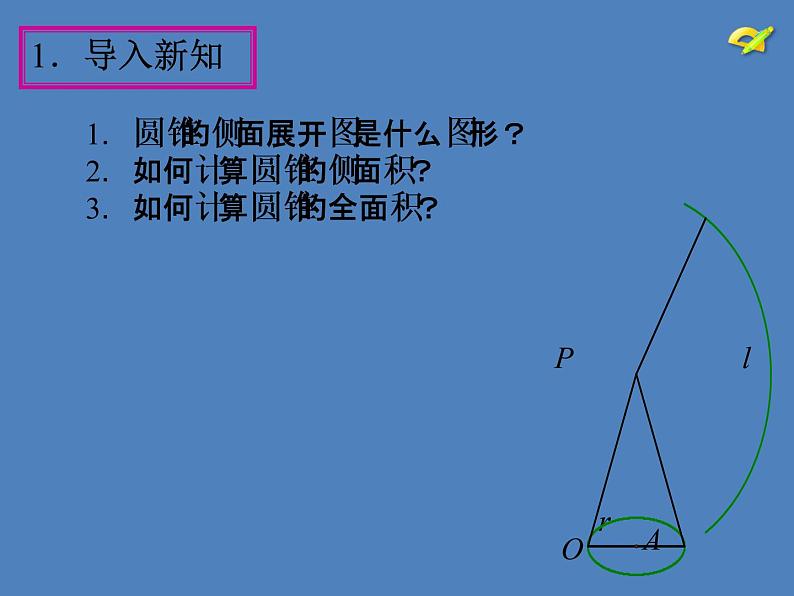
　　1．圆锥的侧面展开图是什么图形？　　2．如何计算圆锥的侧面积？　　3．如何计算圆锥的全面积？
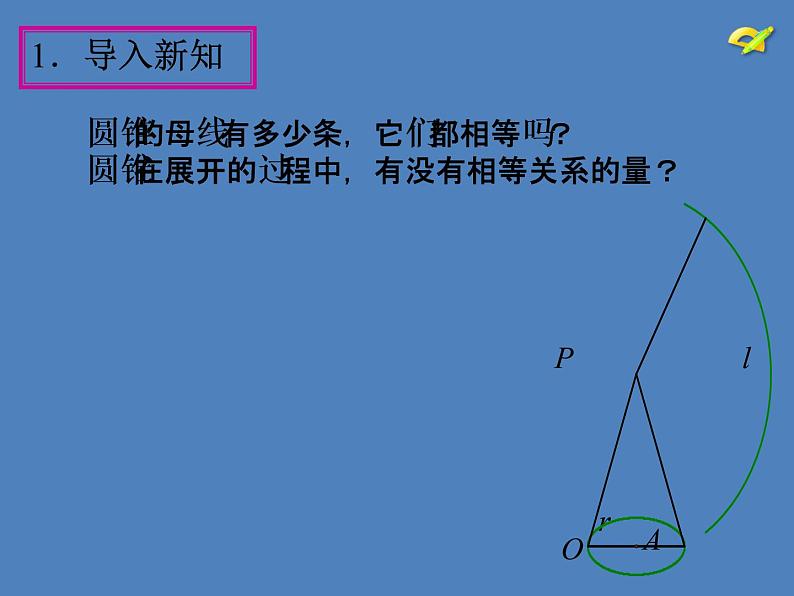
　　圆锥的母线有多少条，它们都相等吗？　　圆锥在展开的过程中，有没有相等关系的量？
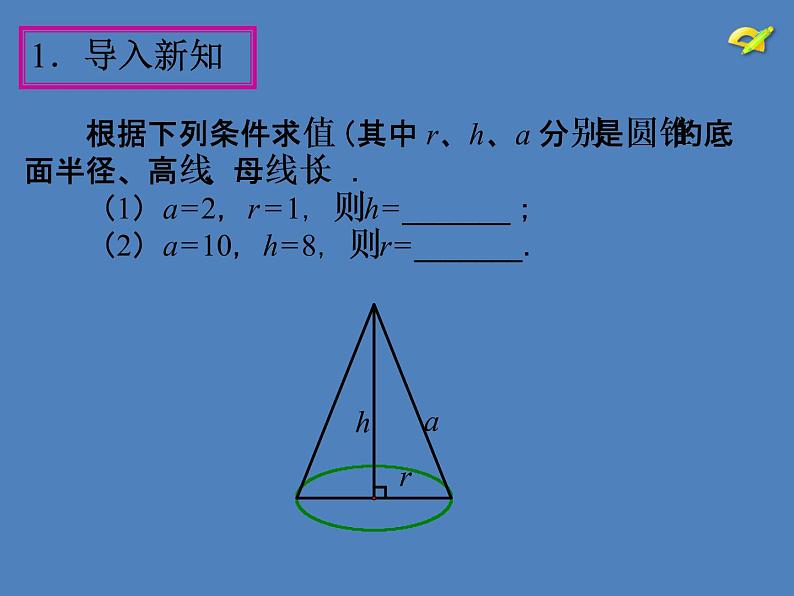
　　根据下列条件求值（其中 r、h、a 分别是圆锥的底 面半径、高线、母线长） ． 　　（1）a = 2，r = 1，则 h = _______； 　　（2）a = 10，h = 8，则 r = _______．
　　蒙古包可以近似地看作由圆锥和圆柱组成．如果想 用毛毡搭建 20 个底面积为 12 m2，高为 3.2 m ，外围高 1.8 m 的蒙古包，至少需要多少平方米的毛毡（π取3.142，结果取整数）？
1、如果扇形的圆心角是230°，那么这个扇形的面积等于这个扇形所在圆的面积的（ ）2、扇形的面积是它所在圆的面积的 ，这个扇形的圆心角的度数是_________°.3、扇形的面积是S，它的半径是r，这个扇形的弧长是（ ）
例1　如图，圆心角为60°的扇形的半径为10厘米，求这个扇形的面积和周长．（π≈3.14）
≈52.33(平方厘米)；
≈ 30.47（厘米）。
解:因为n＝60°，r＝10厘米，所以扇形面积为
1 扇形AOB的半径为12cm,∠AOB=120°,求AB的长和扇形的面积及周长.
例2 如图,当半径为30cm的转动轮转过120°时,传送带上的物体A平移的距离为______.
2小红准备自己动手用纸板制作圆锥形的生日礼帽,如图,圆锥帽底面积半径为9cm,母线长为36cm,请你帮助他们计算制作一个这样的生日礼帽需要纸板的面积为_________.
|--36cm---|
　　（1）圆锥的侧面展开图是什么形状？ 　　（2）如何利用圆锥的侧面展开图求得其侧面积， 进而得到其全面积？
　　教科书第 114 页　练习第 1，2 题；　　教科书习题 24.4　第 9 题．