




人教版数学 八下 第19章单元同步测试提升卷A卷原卷+解析
展开人教版数学 八下 第19章 单元同步测试提升卷A卷
一.选择题(共30分)
1.如图,在同一直角坐标系中作出一次函数与的图象,则二元一次方程组的解是( )
A. B. C. D.
-2-1-cnjy-com
2.如图,函数的图象经过点,则关于的不等式的解集是( )
A. B. C. D.
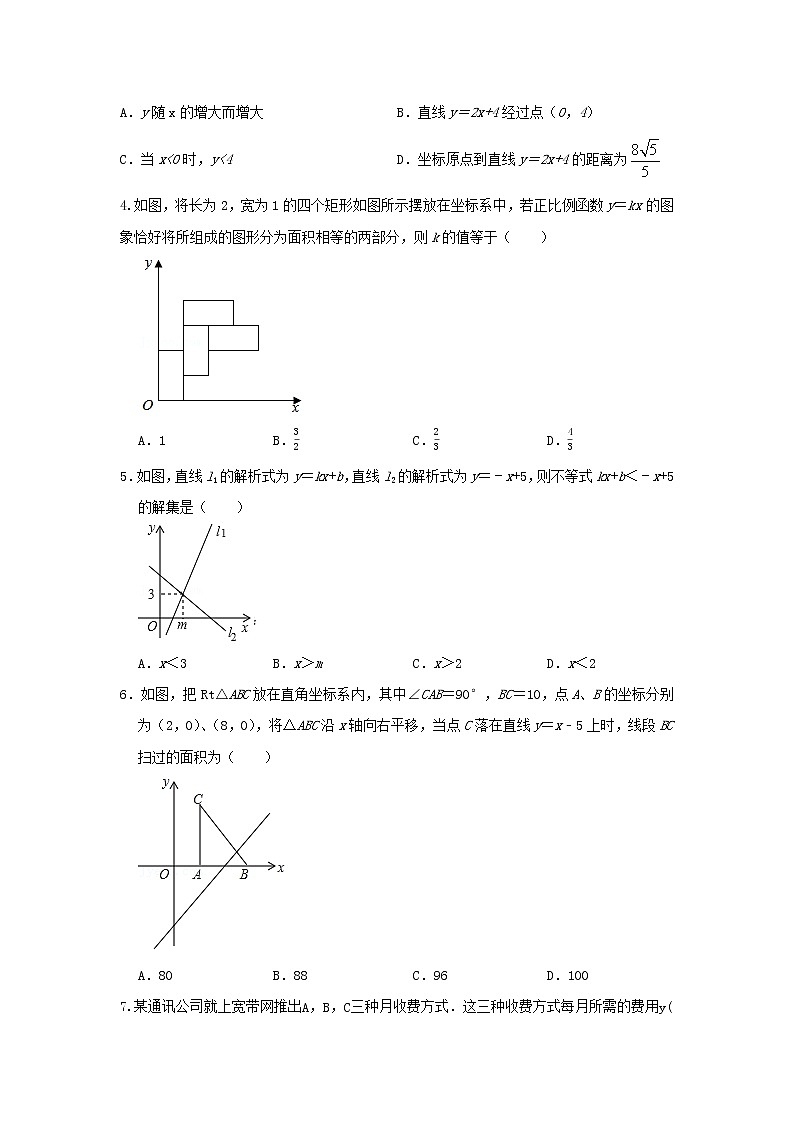
3.一次函数y=2x+4的图象如图所示,则下列说法中错误的是( )
A.y随x的增大而增大 B.直线y=2x+4经过点(0,4)
C.当x<0时,y<4 D.坐标原点到直线y=2x+4的距离为
4.如图,将长为2,宽为1的四个矩形如图所示摆放在坐标系中,若正比例函数y=kx的图象恰好将所组成的图形分为面积相等的两部分,则k的值等于( )
A.1 B. C. D.
5.如图,直线l1的解析式为y=kx+b,直线l2的解析式为y=﹣x+5,则不等式kx+b<﹣x+5的解集是( )
A.x<3 B.x>m C.x>2 D.x<2
6.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,线段BC扫过的面积为( )
A.80 B.88 C.96 D.100
7.某通讯公司就上宽带网推出,,三种月收费方式.这三种收费方式每月所需的费用元与上网时间的函数关系如图所示,则下列判断错误的是
-
每月上网时间不足时,选择方式最省钱
B. 每月上网费用为元时,方式可上网的时间比方式多
C. 每月上网时间为时,选择方式最省钱
D. 每月上网时间超过时,选择方式最省钱
8.若一次函数的图象不经过第二象限,则的取值范围是
- B. C. D.
9.已知一次函数,当时,对应的函数值的取值范围是,则的值为
A. B. C. 或 D. 或
10.如图,在平面直角坐标系中,点,直线交坐标轴于B、C,且,点M在直线上,且,则直线的解析式为( )
A. B. C. D.
二.填空题(共24分)
11.如果关于的一次函数的图象不经过第三象限,那么的取值范围______.
12.,两地相距,甲货车从地以的速度匀速前往地,到达地后停止.在甲出发的同时,乙货车从地沿同一公路匀速前往地,到达地后停止.两车之间的路程与甲货车出发时间之间的函数关系如图中的折线所示.其中点的坐标是,点的坐标是,则点的坐标是______.
13.如图,直线yx+8交y轴于点A,交x轴于点B,C是直线AB上的一个动点,过点C作CD⊥x轴于点D,CE⊥y轴于点E,DE的长的最小值为 .
14.如图所示,已知点N(1,0),一次函数y=﹣x+4的图象与两坐标轴分别交于A,B两点,点M,P分别是线段OB,AB上的动点,则PM+MN的最小值是 .
15.在平面直角坐标系中,直线l:y=x+2与y轴交于点A1,如图所示,依次作正方形OA1B1C1,正方形C1A2B2C2,正方形C2A3B3C3,正方形C3A4B4C4,…,点A1,A2,A3,A4,…在直线l上,点C1,C2,C3,C4,…在x轴正半轴上,则An的坐标是 .
- 如图,已知点,直线与两坐标轴分别交于,两点.点,分别是,上的动点,则周长的最小值是______.
三.解答题(共66分)
17.(6分)已知水池中有立方米的水,每小时抽立方米.
写出剩余水的体积立方米与时间小时之间的函数解析式;
写出自变量的取值范围;
小时后,池中还有多少水?
18.(8分)如图,函数y=﹣2x+3与yx+m的图象交于P(n,﹣2).
(1)求出m、n的值;
(2)直接写出不等式x+m>﹣2x+3的解集;
(3)求出△ABP的面积.
19.(8分).如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k,b的值;
(2)请直接写出不等式kx+b﹣3x>0的解集;
(3)M为射线CB上一点,过点M作y轴的平行线交y=3x于点N,当MN=OD时,求M点的坐标.
20.(10分)甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
(1)求线段对应的函数关系式,并写出x的取值范围;
(2)在轿车追上货车后至到达乙地前,何时轿车在货车前30千米.
21.(10分)如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
(1)写出y与t之间的函数关系式;
(2)通话2分钟应付通话费多少元?通话7分钟呢?
22.(12分)请根据学习函数的经验,对函数的图象与性质进行探究.
(1)在函数中,自变量x的取值范围是____.
(2)下表是x与y的对应值:
x | 0 | 1 | 2 | 3 | |||||
4 | 3 | 2 | 1 | 2 | 3 | m |
①____;
②若,为该函数图象上不同的两点,则____;
(3)在如图的直角坐标系中:
①描出上表中各对对应值的坐标的点,并根据描出的各点,画出该函数的大致图象;
②根据函数图象可得,该函数的最小值为____;
③结合函数图象,写出该函数除②外的一条性质;
(4)若直线l:与函数的图象有交点,请求出交点坐标,并直接写出当时x的取值范围.
23.(12分).如图,一次函数y=kx+b的图象经过点A (﹣2,6),与x轴交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.
(1)求AB的函数表达式;
(2)若点D在y轴负半轴,且满足S△CODS△BOC,求点D的坐标.









