

初中数学第4章 直线与角综合与测试练习
展开(时间80分,满分100分)
班级_________姓名_________学号_________成绩__________
一、单选题(共10题;共30分)
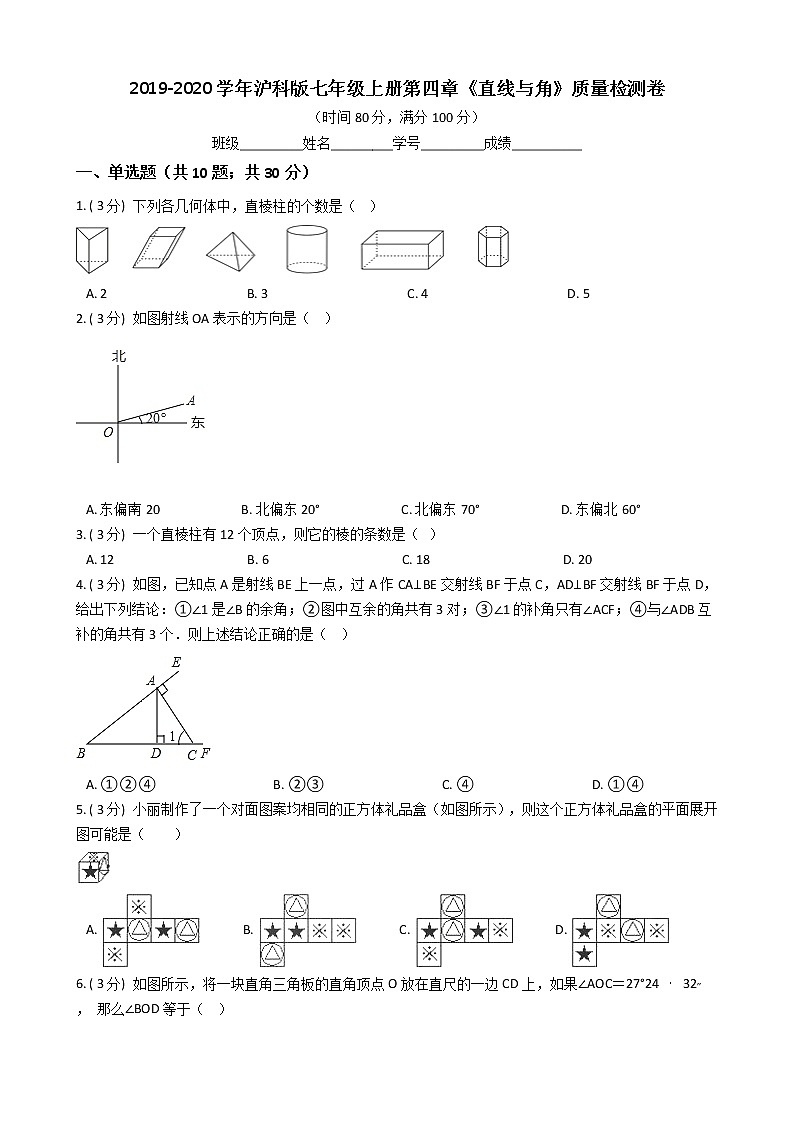
1. ( 3分) 下列各几何体中,直棱柱的个数是( )
A. 2 B. 3 C. 4 D. 5
2. ( 3分) 如图射线OA表示的方向是( )
A. 东偏南20 B. 北偏东20° C. 北偏东70° D. 东偏北60°
3. ( 3分) 一个直棱柱有12个顶点,则它的棱的条数是( )
A. 12 B. 6 C. 18 D. 20
4. ( 3分) 如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:①∠1是∠B的余角;②图中互余的角共有3对;③∠1的补角只有∠ACF;④与∠ADB互补的角共有3个.则上述结论正确的是( )
A. ①②④ B. ②③ C. ④ D. ①④
5. ( 3分) 小丽制作了一个对面图案均相同的正方体礼品盒(如图所示),则这个正方体礼品盒的平面展开图可能是( )
A. B. C. D.
6. ( 3分) 如图所示,将一块直角三角板的直角顶点O放在直尺的一边CD上,如果∠AOC=27°24 , 32,, , 那么∠BOD等于( )
A. 70°24′32″ B. 62°35′28″ C. 52°44′38″ D. 28°24′32″
7. ( 3分) 两个角的和与这两个角的差互补,则这两个角( ).
A. 一个是锐角,一个是钝角; B. 都是钝角; C. 都是直角; D. 必有一个是直角
8. ( 3分) 如图,与∠1互余的角的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
9. ( 3分) 如图,点A、B、C顺次在直线l上,点M是线段AC的中点,点N是线段BC的中点.若想求出MN的长度,那么只需条件( )
A. AB=12 B. BC=4 C. AM=5 D. CN=2
10. ( 3分) 如果时钟上的时针、分针和秒针都是匀速地转动,那么从3时整(3:00)开始,在1分钟的时间内,3根针中,出现一根针与另外两根针所成的角相等的情况有 ( )
A. 1次 B. 2次 C. 3次 D. 4次
二、填空题(共7题;共24分)
11. ( 4分) 70°30′的余角为________度 .
12. ( 4分) 已知,B是线段AD上一点,C是线段AD的中点,若AD=10,BC=3,则AB=________.
13. ( 4分) 为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一现象的原因________.
14. ( 4分) 如图,已知O是线段AB的中点,C是AB的三等分点,OC=2cm, 则AB=________.
15. ( 4分)下列某种几何体从正面、左面、上面看到的形状图都相同,则这个几何体是______(填写序号)
①三棱锥;②圆柱;③球.
16. ( 4分) 在数轴上,点A,O,B分别表示-16,0,14,点P,Q分别从点A,B同时开始沿数轴正方向运动,点P的速度是每秒3个单位,点Q的速度是每秒1个单位,运动时间为t秒.若点P,Q,O三点在运动过程中,其中一点恰好是另外两点为端点构成的线段的三等分点时,则运动时间为_____________秒.
三、解答题(共2题;共46分)
17. ( 5分) 一个角的补角比这个角的余角的2倍还多40°,求这个角的度数.
18. ( 5分) 如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.
19. ( 5分) 如图所示,线段AB=8cm,E为线段AB的中点,点C为线段EB上一点,且EC=3cm,点D为线段AC的中点,求线段DE的长度.
20. ( 5分) 如图,已知OB平分 ∠AOC ,OD平分 ∠COE , ∠AOD=110∘ , ∠BOE=100∘ ,求 ∠AOE 的度数.
21. ( 8分) 观察图形,回答下列问题:
(1)图是由几个面组成的,这些面有什么特征?
(2)图②是由几个面组成的,这些面有什么特征?
(3)图①中共形成了多少条线?这些线都是直的吗?图②呢?
(4)图①和图②中各有几个顶点?
22. ( 8分) 如图,点A、O、B在同一条直线上,∠AOC=∠BOD,OE是∠BOC的平分线.
(1)若∠AOC=46°,求∠DOE的度数;
(2)若∠DOE=30°,求∠AOC的度数.
23. ( 10分) A,B两点在数轴上的位置如图所示,其中点A对应的有理数为-4,且AB=10。动点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒(t>0)。
(1)当t=1时,AP的长为________,点P表示的有理数为________;
(2)当PB=2时,求t的值;
(3)M为线段AP的中点,N为线段PB的中点. 在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长。
参考答案和试题解析部分
一、单选题
1.【答案】B
【解析】【分析】直棱柱由上、下两个底面以及侧面组成;上下两个底面可以是全等的多边形,侧面是矩形.
【解答】直棱柱的侧面应是矩形,符合这个条件的有第一个,第五个和第六个.
故选B.
【点评】本题考查直棱柱的定义,应抓住直棱柱侧面为矩形进行选择.
2.【答案】 C
【解析】【分析】根据方位角的概念,确定射线OA表示的方位角即可.
【解答】根据方位角的概念,射线OA表示的方向是北偏东70°.
故选C.
【点评】解答此题要注意一条射线的方位角有两种表示方法.
3.【答案】C
【解析】【分析】一个直棱柱有12个顶点,说明它的上下底面是两个六边形,从而可以确定它的棱的条数.
直棱柱有12个顶点,一定是六棱柱,所以它的棱的条数是6×3=18个,故选C.
【点评】解答本题的关键是掌握好n棱柱有2n个顶点,有(n+2)个面,有3n条棱.
4.【答案】 D
【解析】【解答】①∠1是∠B的余角,说法正确,故本项正确;②互余的角有:∠1和∠B;∠1和∠CAD;∠B和∠BAD;∠CAD和∠BAD,共4对,原说法错误,故本选项错误;③∠1的补角有:∠ACF、∠EAD,原说法错误,故本项错误;④与∠ADB互补的角有:∠ADF、∠EAC、∠BAC,共3个,说法正确,故本项正确;
综上可得①④正确.
故答案为:D.
【分析】根据互为余角和互为补角的定义可求解。
5.【答案】 A
【解析】【分析】本题考查了正方体的展开与折叠.可以动手折叠看看,充分发挥空间想象能力解决也可以。
【解答】只有相对面的图案相同。
故选A.
6.【答案】 B
【解析】【解答】由题意得,∠AOC+∠AOB+∠BOD=180°,
解得:∠BOD=62°35′28″.
故答案为:B.
【分析】根据平角的定义∠AOC+∠AOB+∠BOD=180°,从而根据∠BOD=180°-∠AOC-∠AOB算出答案。
7.【答案】 D
【解析】【解答】设两个角为α,β.则(α+β)+(α﹣β)=180°,即α=90°.故选D.
【分析】先设两个角为α,β.则(α+β)+(α﹣β)=180°,整理得出这两个角的关系.
8.【答案】C
【解析】【分析】根据三角形的内角和定理,互余的定义,对顶角相等即可判断。
【解答】由图可知∠1+∠DOC=90°,∠1+∠A=90°,∠BOE+∠BOE=90°,∠DOC=∠BOE,
则与∠1互余的角的个数有∠DOC、∠A、∠BOE共3个。
故选C.
【点评】解答本题的关键是熟练掌握三角形的内角和为180°,和为90°的角互为余角。
9.【答案】A
【解析】【解答】解:根据点M是线段AC的中点,点N是线段BC的中点,可知: ,
∴只要已知AB即可.
故选A.
【分析】根据点M是线段AC的中点,点N是线段BC的中点,可知:, 继而即可得出答案.
10.【答案】D
【解析】【解答】解:从3时整(3:00)开始,在1分钟的时间内,3根针中,出现一根针与另外两根针所成的角相等的情况有:
①当秒针转到大约45°的位置时,以及大约225°的位置时秒针平分时针与分针.
②当秒针转到大约180°的位置时,时针平分秒针与分针.
③当秒针转到大约270°的位置时,分针平分秒针与时针.
综上,共4次.
故答案为:D.
【分析】根据题意从3时整,在1分钟的时间内,3根针中,出现一根针与另外两根针所成的角相等的情况有当秒针转到大约45°的位置时,以及大约225°的位置时秒针平分时针与分针;当秒针转到大约180°的位置时,时针平分秒针与分针;当秒针转到大约270°的位置时,分针平分秒针与时针.
二、填空题
11.【答案】19°30′
【解析】【解答】根据余角的定义得:90°-70°30′=19°30′.
故答案为:19°30′.【分析】根据互余两角的和为90°计算.
12.【答案】2或8
【解析】【解答】 解:如图,∵C是线段AD的中点,
∴AC=CD= 12 AD=5,
∴当点B在中点C的左侧时,AB=AC﹣BC=2.
当点B在中点C的右侧时,AB=AC+BC=8.
∴AB=2或8.
【分析】根据题意,正确画出图形,显然此题有两种情况:
当点B在中点C的左侧时,AB=AC﹣BC;
当点B在中点C的右侧时,AB=AC+BC.
13.【答案】两点之间线段最短
【解析】【解答】解:为抄近路践踏草坪原因是:两点之间线段最短. 故答案为:两点之间线段最短.
【分析】根据线段的性质解答即可.
14.【答案】12cm
【解析】【解答】∵AO= 12 AB,AC= 13 AB,∴OC=AO-AC= 16 AB=2cm,∴AB=12cm.故答案为12cm.【分析】根据中点及三等分点的意义得出AO= 12AB,AC= 13AB ,然后根据OC=AO-AC= 16 AB=2cm ,列出方程,求解得出AB的长度 。
15.【答案】③
【解析】解:球的三视图均为全等的圆,
故答案为:③.
16.【答案】 、 、 或 秒.
【解析】【解答】设运动的时间为t(t>0),则点P表示3t-16,点Q表示t+14,
①当点O在线段AB上时,如图1所示.
此时3t-16<0,即t< 163 .
∵点O是线段PQ的三等分点,
∴PO=2OQ或2PO=OQ,
即16-3t=2(t+14)或2(16-3t)=t+14,
解得:t=- 125 (舍去),或t= 187 ;
②当点P在线段OQ上时,如图2所示.
此时0<3t-16<t+14,即 163 <t<15
∵点P是线段OQ的三等分点,
∴2OP=PQ或OP=2PQ,
即2(3t-16)=t+14-(3t-16)或3t-16=2[t+14-(3t-16)],
解得:t= 314 ,或t= 767 ;
③当点Q在线段OP上时,如图3所示.
此时t+14<3t-16,即t>15.
∵点Q是线段OP的三等分点,
∴OQ=2QP或2OQ=QP,
即t+14=2[3t-16-(t+14)]或2(t+14)=3t-16-(t+14),
解得:t= 743 ,或无解.
综上可知:点P,Q,O三点在运动过程中,其中两点为端点构成的线段被第三个点三等分,则运动时间为 187 、 314 、 767 或 743 秒.
故答案为: 187 、 314 、 767 或 743 秒.
【分析】设运动的时间为t(t>0),则点P表示3t-16,点Q表示t+14,需要分类讨论:①当点O在线段AB上时,如图1所示.点O是线段PQ的三等分点,故PO=2OQ或2PO=OQ,从而列出方程,求解并检验即可得出t的值;②当点P在线段OQ上时,如图2所示.点P是线段OQ的三等分点,故2OP=PQ或OP=2PQ,从而列出方程,求解并检验即可得出t的值;③当点Q在线段OP上时,如图3所示.点Q是线段OP的三等分点,故OQ=2QP或2OQ=QP,从而列出方程,求解并检验即可得出t的值,综上所述即可得出答案。
三、计算题
17.【答案】解:设这个角为x°,则其余角为(90﹣x)°,补角为(180﹣x)°,依题意有 180﹣x=2(90﹣x)+40,
解得x=40
【解析】【分析】这类题目要先设出这个角的度数.设这个角为x°,分别写出它的余角和补角,根据题意写出等量关系,解之即可得到这个角的度数.
18.【答案】解:∵∠AOB=90°,OC平分∠AOB
∴∠BOC= 12 ∠AOB=45°
∵∠BOD=∠COD﹣∠BOC=90°﹣45°=45°
∠BOD=3∠DOE
∴∠DOE=15°
∴∠COE=∠COD﹣∠DOE=90°﹣15°=75°
【解析】【分析】根据OC平分∠AOB可求∠BOC的度数,∠BOD与∠BOC互余可求∠BOD,由∠BOD=3∠DOE可求∠DOE,根据∠COE=∠COD﹣∠DOE可求∠COE
19.【答案】解:∵线段AB=8cm , E为线段AB的中点,
∴BE=12AB=4cm,
∴BC=BE−EC=4−3=1cm,
∴AC=AB−BC=8−1=7cm,
∵点D为线段AC的中点,
∴CD=12AC=3.5cm,
∴DE=CD−EC=3.5−3=0.5cm.
【解析】【分析】根据线段中点的定义得出B E = 12 A B = 4 c m ,根据线段的和差由 BC=BE−EC得出BC的长度,进一步由AC=AB−BC得出AC的长度,根据中点的定义得出CD=12AC,最后由D E=CD−EC算出答案 。
20.【答案】 解: ∵OB 平分 ∠AOC ,OD平分 ∠COE ,
∴ 设 ∠EOD=∠DOC=x∘ , ∠AOB=∠COB ,
∵∠AOD=110∘ , ∠BOE=100∘ ,
∴∠AOB=∠BOC=100∘−2x∘ ,
∴∠COD+∠COB+∠AOB=110∘ ,
∴x+100−2x+100−2x=110 ,
解得 x=30 ,
即 ∠EOD=∠DOC=30∘ ,
∴∠AOE=∠AOD+∠DOE=110∘+30∘=140∘
【解析】【分析】此题可以用设未知数的方式表示角的度数之间的关系,根据角平分线的定义 设 ∠EOD=∠DOC=x∘ , ∠AOB=∠COB ,然后根据角的和差得出 ∠AOB=∠COB =100°-2x°,然后根据 ∠COD+∠COB+∠AOB=100°列出方程,求解得出x的值,进而根据∠AOE=∠AOD+∠DOE即可算出答案。
21.【答案】(1)解:图①是由6个面组成的,这些面都是平面
(2)解:图②是由2个面组成的,1个平面和1个曲面
(3)解:图①中共有12条线,这些线都是直的;图②中有1条线,是曲线
(4)解:图①中有8个顶点,图②中只有1个顶点
【解析】【分析】(1)图①是一个长方体,由六个平面组成;
(2)图②是圆锥,由两个面组成,底面是一个平面,侧面是一个曲面;
(3)图①共形成了12条线,这些线作了长方体的棱,都是直的;图②只有一条线,这条线就是底面的圆周,故是曲的;
(4)根据线与线相交成点,这些点是几何体的顶点,故图①中有8个顶点,图②中只有1个顶点。
22.【答案】(1)解:∵∠AOC=46°
∴∠BOC=180º--∠AOC =180º -46º =134º
又∵OE是∠BOC的平分线
∴∠BOE= 12 ∠BOC=67º
又∵∠BOD=∠AOC= =46º
∴∠DOE=∠BOE-∠BOD=67º--46º=21º 。
(2)解:设∠AOC的度数为x,则∠BOD=x,则∠BOE=x+30 º
∵OE是∠BOC的平分线
∴∠BOC=2∠BOE=2(x+30 º)
则有:x+2(x+30 º)=180
解得:x=40 º
∴∠AOC=40º
【解析】【分析】(1)根据角的和差得出∠BOC=180º--∠AOC =180º -46º =134º ,根据角平分线的定义得出∠BOE= 12∠BOC=67º ,然后根据∠DOE=∠BOE-∠BOD算出结果 ;
(2)设∠AOC的度数为x,则∠BOD=x,则∠BOE=x+30 º ,根据角平分线的定义得∠BOC=2∠BOE=2(x+30 º) ,从而得出方程x+2(x+30 º)=180° ,求解得出x的值,即得到∠AOC=40º 。
23.【答案】(1)2;-2
(2)解:当PB=2时,要分两种情况讨论,点P在点B的左侧时,因为AB=10,所以AP=8,所以t=4;点P在点B的是右侧时,AP=12,所以t=6;
(3)解:MN长度不变且长为5.理由如下:因为M为线段AP的中点,N为线段PB的中点,所以MP= 12 AP, NP= 12 BP,所以MN= 12 AB,因为AB=10,所以MN=5
【解析】【解答】(1)因为点P的运动速度每秒2个单位长度,所以当t=1时,AP的长为2,因为点A对应的有理数为-4,AP=2,所以点P表示的有理数为-2;【分析】(1)根据点P的运动速度及时间,可求出点P的运动路程,即AP的长;根据点A表示的数及AP的长,可得出点P表示的数。
(2)根据题意结合数轴可知点P的位置有两种情况:点P在点B的左侧时;点P在点B的是右侧时,先分别求出AP的长,再根据点P的运动速度即可求出t的值。
(3)根据中点的定义证明MN= 12 AB,即可得出线段MN的长度不变且是一个定值。
试卷分析部分
1. 试卷总体分布分析
2. 试卷题量分布分析
3. 试卷难度结构分析
4. 试卷知识点分析
总分:100分
分值分布
客观题(占比)
34(34.0%)
主观题(占比)
66(66.0%)
题量分布
客观题(占比)
11(47.8%)
主观题(占比)
12(52.2%)
大题题型
题目量(占比)
分值(占比)
单选题
10(43.5%)
30(30.0%)
填空题
6(26.1%)
24(24.0%)
计算题
2(8.7%)
10(10.0%)
解答题
2(8.7%)
10(10.0%)
综合题
3(13.0%)
26(26.0%)
序号
难易度
占比
1
容易
43.5%
2
普通
39.1%
3
困难
17.4%
序号
知识点(认知水平)
分值(占比)
对应题号
1
认识立体图形
6(3.8%)
1,3
2
钟面角、方位角
6(3.8%)
2,10
3
点、线、面、体及之间的联系
11(7.0%)
3,21
4
余角、补角及其性质
30(19.1%)
4,6,7,8,11,15,17,18
5
几何体的展开图
3(1.9%)
5
6
角的运算
24(15.3%)
6,7,18,20,22
7
三角形内角和定理
3(1.9%)
8
8
作图—尺规作图的定义
3(1.9%)
9
9
线段的长短比较与计算
8(5.1%)
12,16
10
线段的性质:两点之间线段最短
4(2.5%)
13
11
三角形三边关系
4(2.5%)
13
12
线段的中点
23(14.6%)
14,16,19,23
13
解一元一次方程
4(2.5%)
14
14
角的平分线
18(11.5%)
18,20,22
15
坐标与图形变化﹣平移
10(6.4%)
23
沪科版七年级上册4.4 角课后练习题: 这是一份沪科版七年级上册4.4 角课后练习题,共28页。
初中数学沪科版七年级上册第4章 直线与角综合与测试测试题: 这是一份初中数学沪科版七年级上册第4章 直线与角综合与测试测试题,共9页。试卷主要包含了选择题,填空题,作图题,解答题等内容,欢迎下载使用。
初中数学沪科版七年级上册第4章 直线与角综合与测试单元测试练习题: 这是一份初中数学沪科版七年级上册第4章 直线与角综合与测试单元测试练习题,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。