人教A版 (2019)必修 第一册4.3.1 对数的概念教案及反思

这是一份人教A版 (2019)必修 第一册4.3.1 对数的概念教案及反思，共4页。
课程基本信息
课例编号
2020QJ10SX
RA030
学科
数学
年级
高一
学期
上学期
课题
4.3.1对数的概念
教科书
书名：普通高中教科书数学（A版）必修一
出版社：人民教育出版社 出版日期：2019年 7月
教学人员
姓名
单位
授课教师
杨震涛
北京市一零九中学
指导教师
李颖
北京市东城区教师研修中心
教学目标
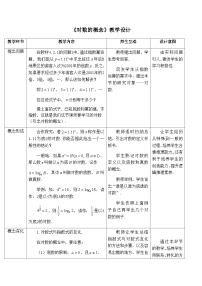
教学目标：
1.初步理解对数的概念，能进行指数式与对数式的互化；
2.了解指数与对数的内在联系，在概念指导下完成对数计算；
3.借助转化思想理解对数本质，培养数学运算和数学抽象的素养。
教学重点：
对数的概念、指数式与对数的互化。
教学难点：
对数符号的理解，以及对数与指数间的联系的认识。
教学过程
时间
教学环节
主要师生活动
1分30秒
温故知新
已有旧知
教师提出问题：
学习指数函数时我们曾讲解过这样一道题目：某地B景区从2001年起游客人次的年增长率为0.11，设经过x年后的游客人次为2001年的y倍，表示x,y的关系，并试求经过多少年游客人次是2001年的2倍，3倍，4倍……？
新知产生
教师点拨：
求解x的值，其实就是已知底数和幂的值，求指数．这就是本节要学习的对数。对数是一种新的运算，由刚才的实际问题可以感受到学习这种运算的必要。
10分钟
探
究
新
知
新知形成
对于形如，求的问题，我们引入新的符号来表示的值.
1.1x=2,那么可以记作=lg1.12,读作以1.1为底2的对数；
2=3，那么可以记作=lg23, 读作以为底的对数；
若 2x=N呢？ ；
.
对数的概念
一般地，如果，那么数x叫做以为底 的对数，记作，其中叫做对数的底数，叫做真数
注意：是对数的符号，类似除法运算的“”，表示一种运算，用它连接运算的对象；
已知底数a和它的幂N求指数的运算,这种运算叫对数运算,只不过对数运算的符号写在数的前面，其运算结果仍是一个实数。
新知特征
指数式与对数式的互化
底数
指数
幂
真数
对数
由指数与对数的等价关系，思考在对数式中，的范围？
.
教师点评：对于的范围源于指数式中对于底数、幂、指数的要求。
2．对数的重要结论：
(1) 当是负数或零时，对数不存在，即负数和零没有对数．
(2)
(3) ．
3. 两种特殊对数
通常，我们将以10为底的对数叫做常用对数，并把
如，
在生活中如充电器的电容的电压关系，物体的自然冷却关系、细胞的繁殖等，为了描述其自然规律，经常会用到无理数2.71828 ……，用e表示这个无理数。
以无理数e=2.71828……为底数的对数，称为自然对数，并把记作
6分钟
典
例
剖
析
例1 指数式与对数式互化：


解：（1） （2）（3）
（4） （5） （6）
通过这组习题同学们感受到指数与对数虽然表达形式不同，但是
两者的本质是一致的，即底数、指数与对数、幂与真数的对应
例2．求下列各式中的x值：
（1）（2）
（3） （4）
解：（1）因为所以
（2）因为
（3）因为
（4）因为
通过将对数运算转化为指数幂运算，求出对数表达式中对应的具体数值，熟悉指数式与对数式间的关系，计算中要注意位置的转换。
5分钟
追
根
溯
源
几乎所有的现代数学书中,对数运算是通过解指数方程来引入的.但是,就对数发明的起源而言，恰恰是相反，先发明了对数而后发明了指数。
事实上,对数是简化繁杂运算的产物.
16世纪时,科学技术尤其是天文学的飞速发展，需要用到大量的大数乘除法运算，这就迫切需要计算技术的改进.当时的数学家们感叹：“没有什么比大数的乘、除、开平方或开立方运算更让数学工作者头痛、更阻碍计算者的了．这不仅浪费时间，而且容易出错．”为了简化数值计算,1614年约翰·奈皮尔利用对应的思想发表《奇妙的对数表的描述》，提供了提高运算速度的方法。
奈皮尔的对应思想类似下表。
我们发现下表的关系满足指数关系，利用以下对应可以方便地算出16×256的值.
首先,在第二行找到16与256;然后找出它们在第一行中对应的数,即4与8,并求它们的和,即12;最后在第一行中找到12,读出其对应的第二行中的数4 096,这就是16×256的值.
用类似的方法也可以计算4096256的数值
纳皮尔将该数称为对数“ｌｏｇａｒｉｔｈｍ”，这个词由希腊文ｌｏｇｏｓ（关系）和ａｒｉｔｈｍｏｓ（数）两词合成，体现对应思想
对数的发明实现了将乘除运算降级为简单的加减运算。
数学家拉普拉斯说过：“对数的发现，因其节约劳力而延长了天文学家的寿命。”
1分钟
课堂小结
1.对数的概念，指数式与对数式的转化；
2.对数的相关结论及运用；
3.对数发明的背景与原理.
课后作业
1. 123页练习1，2，3
2. 阅读教材128-129页了解对数的发明
3. 通过互联网，进一步了解无理数e，常数对数和自然对数