北师大版（2024）七年级下册数学第一章 整式的乘除 全章课件

这是一份北师大版（2024）七年级下册数学第一章 整式的乘除 全章课件，共60页。
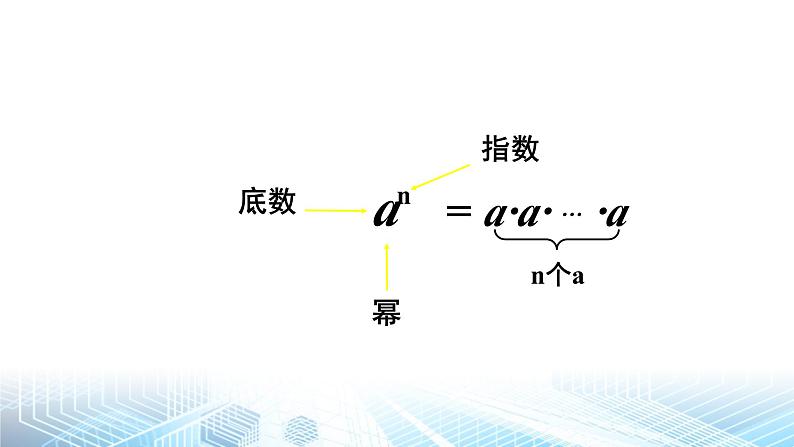
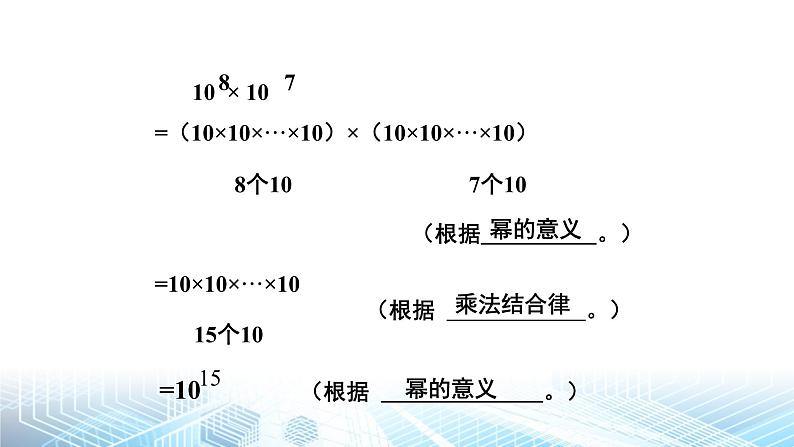
1 同底数幂的乘法第一章 整式的乘除北师大版（2024）七年级下册数学指数幂底数复习旧知 光在真空中的速度大约是3×108m/s，太阳系以外距离地球最近的恒星是比邻星，它发出的光到达地球大约需要4.22年。 一年以3×107 秒计算，比邻星与地球的距离约为多少千米？讲授新课幂的意义幂的意义（根据 。）（根据 。）（根据 。）乘法结合律 1.计算下列各式： （1）102×103; （2）105×108; （3）10m×10n（m，n都是正整数）.你发现了什么？这个结论是否具有一般性？如果底数同样也是字母呢？ am · an等于什么（m,n都是正整数)?为什么？=am+n不变相加同底数幂相乘,底数 ,指数 .不变相加am · an · ap 等于什么？你是怎样做的？与同伴交流判断（正确的打“√”，错误的打“×”） x4·x6=x24 ( 　) （2） x·x3=x3 ( 　)(3) x4+x4=x8 (　 ) (4) x2·x2=2x4 (　 )(5)(－x)2 · (－x)3 = (－x)5 (　 ) (6)a2·a3－ a3·a2 = 0 ( 　 ) (7)x3·y5=(xy)8 ( 　 ) (8) x7+x7=x14 ( 　 ) √√××××××对于计算出错的题目，你能分析出错的原因吗？试试看！ 例2 光在真空中的速度约为3×108m/s，太阳光照射到地球大约需要5×102s. 地球距离太阳大约有多远？解： 3×108×5×102=15×1010=1.5×1011(m)地球距离太阳大约有1.5×1011m. 1.计算： （1）52×57; （2）7×73×72; （3）-x2·x3； （4）(-c)3·(-c)m. 2.一种电子计算机每秒可做4×109次运算，它工作5×102s可做多少次运算？ 3.解决本节课一开始比邻星到地球的距离问题.课堂练习4.把下列各式写成幂的形式 课后小结完成课本习题1.1中所有习题拓展作业： 你能尝试运用今天所学的同底数幂的乘法解决下面的问题吗课后作业2 幂的乘方与积的乘方（第1课时）第一章 整式的乘除北师版七年级下册同底数幂乘法的运算性质：am · an= am+nam·an= am+n同底数幂相乘,底数不变,指数相加.复习旧知 乙正方体的棱长是 2 cm, 则乙正方体的体积 V乙= cm3 可以看出，V甲 是 V乙 的 倍8125即 53 倍 边长比的 甲正方体的棱长是乙正方体的 5 倍，则甲正方体的体积 V甲= cm31000立方正方体的体积之比=情景导入 地球、木星、太阳可以近似地看做是球体 .木星、太阳的半径分别约是地球的10倍和102倍，它们的体积分别约是地球的多少倍？103倍(102)3倍你知道(102)3等于多少吗？(102)3=102×102×102=102+2+2=102×3=106(根据 ).(根据 ).同底数幂的乘法幂的意义讲授新课=am·am· … ·am做一做：计算下列各式，并说明理由 . (1) (62)4 ; (2) (a2)3 ; (3) (am)2 ; (4) (am)n .解：(1) (62)4 (2) (a2)3(3) (am)2= 62·62· 62·62=62+2+2+2=68= a2·a2·a2=a2+2+2=a6=am·am=am+mn(4) (am)n=amn=am+m+ … +mn幂的乘方，底数 ，指数 . (am)n=amn (m,n都是正整数)不变相乘幂的乘方法则落实基础 例1 计算：（1）(102)3 ; (2) (b5)5 ; （2）(an)3; (4) －(x2)m ; (5) (y2)3 · y ; (6) 2(a2)6 － (a3)4 .2. 计算：(1) (103)3 ; (2) －(a2)5 ; (3) (x3)4 · x2 ;(4) [(－x)2 ]3 ; (5) (－a)2(a2)2; (6) x·x4 – x2 · x3 . 随堂练习：1. 判断下面计算是否正确？如果有错误请改正：(1) (x3)3 = x6 ; (2)a6 · a4 = a24 .课堂练习同底数幂相乘,底数不变,指数相加.幂的乘方，底数不变，指数相乘.课堂小结完成课本习题1.2中1、2拓展作业： 你能尝试运用今天所学的知识解决下面的问题吗(1)填空： [（a－b）3 ]2＝（b－a ）( )(2)若4﹒8m﹒16m ＝29 ，求m的值课后作业2 幂的乘方与积的乘方（第2课时）第一章 整式的乘除北师版七年级下册2.同底数幂的乘法运算法则：3.幂的乘方运算法则:复习旧知 地球可以近似地看做是球体，地球的半径约为6×103 km，它的体积大约是多少立方千米? 那么， (6×103)3 =？ 这种运算有什么特征？讲授新课(1) 根据幂的意义，(ab)3表示什么?=a·a·a · b·b·b=a3·b3(2)由 (ab)3=a3b3 出发, 你能想到更为一般的公式吗? anbn(ab)3=ab·ab·ab不妨先思考(ab)3=？(ab)n = ab·ab·……·ab ( ) =(a·a·……·a) (b·b·……·b) ( ) =an·b ( ) 幂的意义乘法交换律、结合律 幂的意义(ab)n = an·bn积的乘方乘方的积（m,n都是正整数）积的乘方法则积的乘方,等于每一因数乘方的积. 三个或三个以上的积的乘方，是否也具有上面的性质? 怎样用公式表示?(abc)n=an·bn·cn巩固新知例2 计算： (1) (3x)2 ; (2) (-2b)5 ; (3) (-2xy)4 ; (4) (3a2)n . 引例：地球可以近似地看做是球体，地球的半径约为6×103 km，它的体积大约是多少立方千米? 9.05×1011(千米3)≈ 随堂练习： 1.下面的计算是否正确？如有错误请改正： (1) (ab4)4 = ab8 ; (2) (-3pq)2 = –6p2q2 2. 计算： (1) (- 3n)3 ; (2) (5xy)3 ; (3) –a3 +(–4a)2 a 公示逆用(ab)n = an·bn （m,n都是正整数）反向使用:an·bn = (ab)n (am)n= (m，n都是正整数)幂的意义:(ab)n = an·bn（m，n都是正整数）积的乘方运算法则am+namn(m，n都是正整数)=an你学过的幂的运算有哪些?课堂小结完成课本习题1.3中1、2、5、6拓展作业： 你能用几何图形直观的解释 （3b）2=9b2吗？ 课后作业3 同底数幂的除法（第1课时）第一章 整式的乘除北师版七年级下册1.同底数幂的乘法运算法则：2.幂的乘方运算法则:前面我们学习了哪些幂的运算? 在探索法则的过程中我们用到了哪些方法？ 3.积的乘方运算法则复习旧知 一种液体每升含有1012个有害细菌，为了试验某种杀菌剂的效果,科学家们进行了实验,发现1滴杀虫剂可以杀死109个此种细菌， （1）要将1升液体中的有害细菌全部杀死，需要这种杀菌剂多少滴？（2）你是怎样计算的？（3）你能再举几个类似的算式吗？情景导入=10×10×101.计算你列出的算式2.计算下列各式，并说明理由（m>n） (1)10m÷10n； (2)(-3)m÷(-3)n；3.你能用字母表示同底数幂的除法运算法则并说明理由吗？讲授新课同底数幂相除，底数 ，指数 .归纳法则 不变相减am ÷ an =am-n(a≠0，m,n都是正整数，且m＞n）巩固落实 例1 计算：(1) a7÷a4； (2) (－x)6÷(－x)3；(3) －m8÷m2； (4) (xy)4÷(xy) ；(5) b2m+2÷b2； (6) (m+n)8÷(m+n)3； 做一做： 3 213210-1-2-30-1-2-3猜一猜： 你是怎么想的？与同伴交流 0-1-2-30-1-2-3猜一猜： 你有什么发现？能用符号表示吗？我们规定：a 0 = 1 (a≠0） a - p = —— (a≠0，p是正整数）a p 1 你认为这个规定合理吗？为什么？例2 计算： 用小数或分数分别表示下列各数：(1)10-3； (2) 70×8-2； (3) 1.6×10-4； 议一议： 计算下列各式，你有什么发现？与同伴交流 (1) 7-3÷7-5； (2) 3-1÷36；(3) (—)－5÷(—)2 ； (4) (-8)0÷(-8)-2 ； 我们前面学过的运算法则是否也成立呢？ 2211只要m，n都是整数，就有am÷an=am-n成立!反馈练习： 下面的计算是否正确？如有错误请改正 (1) b6÷b2 =b3 ； (2) a10÷a-1 =a9 ； (3) (-bc)4÷(-bc)2 = -b2c2 ； (4) xn+1÷x2n+1 =x-n .反馈练习： 计算 (1) (-y)3÷(-y)2 ； (2) x12÷x-4 ； (3) m÷m0 ； (4) (-r)5÷r 4 ； (5) -kn÷kn+2 ； (6) (mn)5÷(mn) ；拓展延伸： (1) (a - b)8÷(b - a)3 (2) (-38)÷(-3)4这节课你学到了哪些知识？现在你一共学习了哪几种幂的运算？它们有什么联系与区别？谈谈你的理解我们在探索运算法则的过程中用到了哪些方法？课堂小结完成课本习题1.4预习作业：1）纳米是一种长度单位，1米=1,000,000,000纳米，你能用科学记数法表示1,000,000,000吗？反过来，1纳米等于多少米呢？你能用今天学的知识解决吗？这个结果还能用科学记数法表示吗？2）你知道生物课中接触的洋葱表皮细胞的直径是多少吗？照相机的快门时间是多长呢？中彩票头奖的可能性是多大？头发的直径又是多少呢？生活中你还见到过哪些较小的数？请你查阅资料，下节课与同伴交流.课后作业3 同底数幂的除法（第2课时）第一章 整式的乘除北师版七年级下册 纳米是一种长度单位， 1米=1,000,000,000纳米，你能用科学记数法表示1,000,000,000吗？1米=1×109 纳米复习旧知 在用科学记数法表示数据时，我们要注意哪些问题？a× 10n (其中1≤a＜10,n是正整数）你知道吗： 洋葱表皮细胞的直径是多少？ 照相机的快门时间是多长呢？ 中彩票头奖的可能性是多大？ 头发的直径又是多少呢？ 生活中你还见到过哪些较小的数？ 能用科学记数法表示这些数吗？请你与同伴交流讲授新课 一般地，一个小于1的正数可以用科学记数法表示为：怎样确定a和n？a× 10n (其中1≤a＜10,n是负整数）1.用科学记数法表示下列各数： 0.000 000 000 1= 0.000 000 000 002 9= 0.000 000 001 295= 巩固落实 2.下面的数据都是用科学记数法表示的，请你用小数把它们表示出来: 7×10-5= 1.35×10-10= 2.657×10-16= 7×10-5与7-5有什么区别？感受数据 1. PM2.5是指大气中直径小于或等于2.5μm的颗粒物，也称为可入肺颗粒物.虽然他们的直径还不到人的头发丝粗细的二十分之一，但它们含有大量的有毒、有害物质，并且在大气中停留的时间长、输送距离远，因而对人体健康和大气环境质量有很大的危害. 假设一种可入肺颗粒物的直径约为2.5μm，相当于多少米？ 多少个这样的颗粒物首尾连接起来能达到1m？与同伴交流 2. 估计1张纸的厚度大约是多少厘米.你是怎样做的？与同伴交流基础练习：（1）用科学记数法表示下列各数，并在计算器上表示出来： 0.000 000 72； 0.000 861； 0.000 000 000 342 5课堂练习基础练习：（2）1个电子的质量是：0.000 000 000 000 000 00 000 000 000 911g， 用科学记数法表示为 g； 冠状病毒的直径为1.2×102 纳米， 用科学记数法表示为______________米变式练习：（1）每个水分子的质量是3×10-26g，用小数表示为 ； 每个水分子的直径是4×10-10m，用小数表示为 . （2）拓展延伸： 如果一滴水的质量约为 0.05g，请根据（1）中提供的数据回答：①一滴水中大约有多少个水分子？用科学记数法表示 .②如果把一滴水中的水分子依次排成一列（中间没有空隙），能排多少米？用科学记数法表示 .这节课你学到了哪些知识？用科学记数法表示小于1的正数与表示大于10的数有什么相同之处？有什么不同之处？用科学记数法表示容易出现哪些错误？你有哪些经验？与同伴交流.在估测微小事物时你用到了哪些方法和策略？课堂小结完成课本习题1.5拓展作业： 阅读课本“读一读”，你想了解更多的有关纳米技术或微小世界中的有趣问题吗？请你查阅资料，制作成手抄报，一周后带来与同学分享.课后作业4 整式的乘法（第1课时）第一章 整式的乘除北师版七年级下册运用幂的运算性质计算下列各题： 复习旧知七年级三班举办新年才艺展示，小明的作品是用同样大小的纸精心制作的两幅剪贴画，如下图所示，第一幅画的画面大小与纸的大小相同，第二幅画的画面在纸的上、下方各留有 的空白。xm1.2xm情景导入（1） 第一幅画的画面面积是多少平方米？第二幅呢？你是怎样做的？（2） 若把图中的1.2x改为mx,其他不变，则两幅画的面积又该怎样表示呢？1、 3a2b · 2ab3 和 (xyz) ·y2z又等于什么？你是怎样计算的？2、如何进行单项式乘单项式的运算？3、在你探索单项式乘法运算法则的过程中，运用了哪些运算律和运算法则？ 讲授新课探索规律：单项式乘法的法则： 单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式。例1 计算：例题解析：（1）进行单项式乘法，应先确定结果的符号，再把同底数幂分别相乘，这时容易出现的错误是将系数相乘与相同字母指数相加混淆；（2）不要遗漏只在一个单项式中出现的字母，要将其连同它的指数作为积的一个因式；知识加油站：（3）单项式乘法法则对于三个以上的单项式相乘同样适用；（4）单项式乘以单项式，结果仍为单项式。 完成课本15页：随堂练习 延伸拓展： 一家住房的结构如图示，房子的主人打算把卧室以外的部分全都铺上地砖，至少需要多少平方米的地砖？如果某种地砖的价格是a元/平方米，那么购买所需地砖至少需要多少元？计算： ① ② ③ ④ ⑤课堂练习本节课你学到了什么？发现了什么？有什么收获？还存在什么没有解决的问题？课堂小结1. 习题1.62. 拓展探究：课后作业4 整式的乘法（第2课时）第一章 整式的乘除北师版七年级下册1. 计算： 2.写一个多项式，并说明它的次数和项数 复习旧知—xm 才艺展示中，小颖也作了一幅画，所用纸的大小如图所示，她在纸的左、右两边各留了—xm的空白，这幅画的画面面积是多少？mx mx m181818—xm情景导入问题1：ab·(abc+2x) 和c2·(m+n-p)等于什么？你是怎样计算的？问题2： 如何进行单项式与多项式相乘的运算？单项式与多项式相乘的法则：单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加。讲授新课例2 计算： 应用新知：变式训练：1、计算：2、计算： 3、1.计算(1)(3x－1)(4x＋5)； (2)(－4x－y)(－5x＋2y)2．解方程： 3．已知ab2=6，求 的值。课堂练习4.计算：课堂练习本节课学习了哪些知识？领悟到哪些解决问题的方法？感触最深的是什么？对于本节课的学习还有什么困惑？课堂小结1.习题1.72.拓展作业：课后作业4 整式的乘法（第3课时）第一章 整式的乘除北师版七年级下册计算： （1）（2）复习旧知 图1-1是一个长和宽分别为m，n的长方形纸片，如果它的长和宽分别增加a，b，所得长方形（图1-2）的面积可以怎样表示？情境导入1、你能说出这一步运算的道理吗？2、 结合这个算式 (m+a)(n+b)=mn+mb+an+ab你能说说如何进行多项式与多项式相乘的运算？讲授新课单项式与多项式相乘的法则： 单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加。探究尝试：例3 计算： 应用新知：（1）（2）（3） 综合练习：（1） （2）变式训练： 1、计算： （1）（2）2、计算：3、若 求m，n的值.计算： （1） （2）课堂练习本节课学习了哪些知识？领悟到哪些解决问题的方法？感触最深的是什么？对于本节课的学习还有什么困惑？课堂小结1.习题1.82.拓展作业：解方程3.预习作业：两项式乘以两项式，结果可能是四项吗？可能是三项吗？可能是两项吗？请你举例说明 课后作业5 平方差公式（第1课时）第一章 整式的乘除北师版七年级下册多项式乘多项式法则 多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加（m+b)(n+a)=mn+ma+bn+ba复习旧知探究规律计算下列各题：（1）(x+2)(x－2) （2）(1+3a)(1－3a)（3）(x+5y)(x－5y)（4）(2y+z)(2y－z)观察以上算式及其运算结果，你有什么发现？再举两例验证你的发现。平方差公式： (a+b)(a−b)＝a2−b2讲授新课练一练判断下面计算是否正确（1） = （ ）（2）(3x－y)(－3x+y)=9x2－y2 （ ） （3）(m+n)(－m－n)=m2－n2 （ )×××例1利用平方差公式计算：（1）(5+6x)(5－6x)（2）(x－2y)(x+2y)（3）(－m+n)(－m－n)练一练利用平方差公式计算：（1） (a+2)(a－2) （2）(3a+2b)(3a－2b)例2利用平方差公式计算：（1） （2）(ab+8)(ab－8) 练一练利用平方差公式计算：（1） （2）(－mn+3)(－mn－3)想一想(a−b)(−a−b)=？你是怎样做的？ 计算 1、 (5m－n)(－5m－n) 2、 (a+b)(a－b)(a2+b2)利用平方差公式计算：（1）(－x－1)(1－x)（2）(0.3x+2y)(0.3x－2y) （3）课堂练习 分享你的收获， 交流你的困惑。课后小结 1. 必做题：教材习题1.9 2. 选做题： 你能用图形来验证平方差公式吗？课后作业5 平方差公式（第2课时）第一章 整式的乘除北师版七年级下册计算：（1）(102)4 ; (2) (b5)2 ; （3）(an)6; (4) －(x2)n; (5) (y2)4 · y ; (6) 2(a2)6 + (a3)4 .复习旧知 1、平方差公式： (a+b)(a－b)=a2－b2 2、公式的结构特点： 左边是两个二项式的乘积，即两数和与这两数差的积；右边是两数的平方差。3、应用平方差公式的注意事项： 1）注意平方差公式的适用范围 2）字母a、b可以是数，也可以是整式 3）注意计算过程中的符号和括号利用平方差公式计算：（1） (a+2)(a－2) （2）(3a+2b)(3a－2b)（3）(ab+8)(ab－8)利用平方差公式计算：（1）(－x－1)(1－x)（2）(0.3x+2y)(0.3x－2y) （3）活动探究一图1-5如图1-5，边长为a的大正方形中有一个边长为b的小正方形.讲授新课图1-5（1）请表示图1-5中阴影部分的面积（2）小颖将阴影部分拼成了一个长方形，如图1-4，这个长方形的长和宽分别是多少？你能表示出它的面积吗？（3）比较（1）（2）的结果，你能验证平方差公式吗？活动探究二1、计算下列各组算式，并观察它们的共同特点 7×9= 11×13= 79×81= 8×8= 12×12= 80×80=2、从以上过程中，你发现了什么规律？3、请用字母表示这一规律，你能说明它的正确性吗？例3 用平方差公式进行计算：（1）103×97 ； （2）118×122（100+3）（100-3）（120-2）（120+2）练一练计算：（1）704×696 ； （2）9.9 ×10.1例4 计算：（1）a2(a+b)(a－b)+a2b2 （2）(2x-5)(2x+5)-2x(2x-3)练一练计算：（1）(x+2y)(x－2y)+(x+1)(x－1)（2）x(x-1)- 计算：1） 2001×1999 -20002 2）(3mn+1)(3mn-1)-8m2n23） - （x+8）课堂练习 本节课你有哪些收获？ 还有那些困惑？课堂小结 1. 教材习题1.10 2. 拓展作业： 计算(21+1)( 22+1)(24+1)(28+1)(216+1)(232+1)(264+1)课后作业6 完全平方公式（第1课时）第一章 整式的乘除北师版七年级下册公式的结构特征:左边是a2 − b2; 两个二项式的乘积,平方差公式 对于一般两个二项式的积, 看准有无相等的“项”和符号相反的“项”; 仅当把两个二项式的积变成公式标准形式后，才能使用平方差公式。 (a+b)(a−b)=即两数和与这两数差的积.右边是两数的平方差.复习旧知 一块边长为a米的正方形实验田，图1—6 因需要将其边长增加 b 米。 形成四块实验田，以种植不同的新品种(如图1—6). 用不同的形式表示实验田的总面积, 并进行比较. (a+b) ；2a2+ab+ab+b2.(a+b)2=a2+ab+b2.2情境导入 完全平方公式的证明(1) 你能用多项式的乘法法则来说明它成立吗?(a+b)2=a2+2ab+b2 ;(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2;(2)a2 −2ab+b2.小颖写出了如下的算式:(a−b)2=[a+(−b)]2她是怎么想的?利用两数和的完全平方公式推证公式= 2 + 2 + 2 aa(−b)(−b)=a22ab−b2.+你能继续做下去吗?讲授新课 初 识 完全平方公式(a+b)2 = a2+2ab+b2 .(a−b)2 = a2−2ab+b2 .a2abb2结构特征:左边是的平方;二项式右边是a2 +b2 a2 +b2 (两数和 )(差)(a+b)2=a2−ab−b(a−b)=a2−2ab+b2 .=(a−b)2a−ba−bb(a−b)(a−b)2a2+2ab+b2a+ba−b两数的平方和+加上−(减去)2ab2ab这两数乘积的两倍.(a−b)2 = a2−2ab+b2语言表述:两数和 的平方 等于这两数的平方和 加上 这两数乘积的两倍.22(a−b)2 = a2−2ab+b2(差)(减去) 例1 利用完全平方公式计算：(1) (2x−3)2 ； (2) (4x+5y)2 ; (3) (mn−a)2 使用完全平方公式与平方差公式的使用一样, 先把要计算的式子与完全平方公式对照, 明确个是 a , 哪个是 b.第一数2x4x22x的平方,( )2−减去2x第一数与第二数−2x3•乘积的2倍,•2加上+第二数3的平方.2=−12x+9 ;3 (1) ( x − 2y)2 ； (2) (2xy+ x )2 ;1、计算：(3) (n +1)2 − n2.课堂练习 2. 指出下列各式中的错误，并加以改正： (1) (2a−1)2＝2a2−2a+1; (2) (2a+1)2＝4a2 +1； (3) (a−1)2＝a2−2a−1. 3.利用完全平方公式计算： (1) (－1－2x)2 ； (2) (－2x+1)21. 注意完全平方公式和平方差公式不同：形式不同．结果不同：完全平方公式的结果是三项 即 (a b)2＝a2 2ab+b2;平方差公式的结果是两项 即 (a+b)(a−b)＝a2−b2.2. 在解题过程中要准确确定a和b，对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2。课堂小结上交作业：教材习题1.11、1.12； 课后作业6 完全平方公式（第2课时）第一章 整式的乘除北师版七年级下册2. 想一想：（1）两个公式中的字母都能表示什么? （2）完全平方公式在计算化简中有些什么作用?（3）根据两数和或差的完全平方公式，能够计算多个数的和或差的平方吗?1. (a+b) 2=a2+2ab+b2 (a－b) 2=a2－2ab+b2 完全平方公式：复习旧知做一做 有一位老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待他们。来一个孩子，老人就给这个孩子一块糖，来两个孩子，老人就给每个孩子两块糖，来三个，就给每人三块糖，……(1) 第一天有 a 个男孩一起去了老人家，老人一共给了这些孩子多少块糖？讲授新课做一做 有一位老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待他们。来一个孩子，老人就给这个孩子一块糖，来两个孩子，老人就给每个孩子两块糖，来三个，就给每人三块糖，……(2) 第二天有 b 个女孩一起去了老人家，老人一共给了这些孩子多少块糖？b2做一做 有一位老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待他们。来一个孩子，老人就给这个孩子一块糖，来两个孩子，老人就给每个孩子两块糖，来三个，就给每人三块糖，……(3)第三天这(a + b)个孩子一起去看老人，老人一共给了这些孩子多少块糖？(a+b)2做一做 有一位老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待他们。来一个孩子，老人就给这个孩子一块糖，来两个孩子，老人就给每个孩子两块糖，来三个，就给每人三块糖，……(4)这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多？多多少？为什么？(a+b)2-(a2+b2)=a2+2ab+b2-a2-b2=2ab简单应用：例2 利用完全平方公式计算： (1) 1022 ; (2) 1972 . (1) 962 ； (2) 2032 .巩固练习：综合应用 例3 计算： (1) (x+3)2 - x2 (2) (x+5)2–(x-2)(x-3) (3) (a+b+3)(a+b-3)综合应用 巩固练习：（1）(a－b+3)(a－b－3)（2）(x－2)(x+2) －(x+1)(x－3)（3）(ab+1)2－ (ab－1)2（4）(2x－y)2－4(x－y)(x+2y)1. 完全平方公式的使用：在做题过程中一定要注意符号问题和正确认识a、b表示的意义，它们可以是数、也可以是单项式，还可以是多项式，所以要记得添括号.2. 解题技巧：在解题之前应注意观察思考，选择不同的方法会有不同的效果，要学会优化选择.课堂小结教材习题1.12 联系拓广：课后作业联系拓广：1.如果把完全平方公式中的字母“a”换成“m+n”，公式中的“b”换成“p”，那么 (a+b)2 变成怎样的式子? (a+b)2变成(m+n+p)2。 怎样计算(m+n+p)2呢? (m+n+p)2=[(m+n)+p]2逐步计算得到： =(m+n)2+2(m+n)p+p2=m2+2mn+n2+2mp+2np+p2=m2+ n2 +p2+2mn+2mp+2np 把所得结果作为推广了的完全平方公式，试用语言叙述这一公式联系拓广：2.已知:a+b=5,ab=-6,求下列各式的值(1)(a+b)2 (2)a2+b2若条件换成a-b=5,ab=-6,你能求出a2+b2的值吗?7 整式的除法（第1课时）第一章 整式的乘除北师版七年级下册1.同底数幂的除法同底数幂相除，底数不变，指数相减。2.单项式乘单项式法则单项式与单项式相乘，把它们的系数，相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式。复习旧知 学习了今天的知识，我们就能解决这个问题了！你知道吗？情景导入你能计算下列各题吗？如果能，说说你的理由。讲授新课方法1：利用乘除法的互逆探究方法小结方法2：利用类似分数约分的方法约分时，先约系数，再约同底数幂，分子中单独存在的字母及其指数直接作为商的因式。探究方法小结单项式与单项式相除的法则单项式相除，把系数，同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的因式。知识要点系数相乘系数相除同底数幂相乘同底数幂相除其余字母不变连同其指数作为积的因式只在被除式里含有的字母连同其指数一起作为商的因式对比学习例1 计算：试一试解：注意运算顺序：先乘方，再乘除，最后算加减 如图所示，三个大小相同的球恰好放在一个圆柱形盒子里，三个球的体积占整个盒子容积的几分之几？做一做课本随堂练习课堂练习解：答：光速大约是声速的1000000倍，即100万倍。现在你会了吗？1. 单项式与单项式相除的法则单项式相除，把系数，同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的因式2. 对比的学习方法谈谈你的收获课堂小结1.基础作业：习题1.13知识技能 1，2，52.拓展作业：在一次水灾中，大约有2.5×105个人无家可归。假若一顶帐篷占地100 m2 ，可以安置40个床位，为了安置所有无家可归的人，需要多少顶帐篷？这些帐篷大约占多大地方？估计你学校的操场中可以安置多少人？要安置这些人，大约要多少个这样的操场？课后作业7 整式的除法（第2课时）第一章 整式的乘除北师版七年级下册单项式相除，把系数，同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的因式。2.单项式与单项式相除的法则1.同底数幂的除法复习旧知 图（1）的瓶子中盛满了水，如果将这个瓶子中的水全部倒入图（2）的杯子中，那么一共需要多少个这样的杯子？（单位：cm）你知道需要多少杯子吗？情景导入计算下列各题，说说你的理由。讲授新课方法1：利用乘除法的互逆方法2：类比有理数的除法由有理数的除法类比得到多项式除以单项式法则多项式除以单项式，先把这个多项式的每一项分别除以单项式，再把所得的商相加。知识要点例3 计算：试一试解：小明在爬一小山时，第一阶段的平均速度为v，所用时间为 t1；第二阶段的平均速度为 v，所用时间为 t2.下山时，小明的平均速度保持为4v．已知小明上山的路程和下山的路程是相同的，问小明下山用了多长时间？做一做你能说出上面题目错误的原因吗？试试看想一想，下列计算正确吗？课本随堂练习课堂练习现在你会了吗？ 图（1）的瓶子中盛满了水，如果将这个瓶子中的水全部倒入图（2）的杯子中，那么一共需要多少个这样的杯子？（单位：cm）解：多项式除以单项式法则多项式除以单项式，先把这个多项式的每一项分别除以单项式，再把所得的商相加。课堂小结1.习题1.14知识技能 12.完成本章知识结构图课后作业感谢聆听