湘教版（2024）九年级上册3.4 相似三角形的判定与性质示范课课件ppt

这是一份湘教版（2024）九年级上册3.4 相似三角形的判定与性质示范课课件ppt，文件包含341相似三角形的判定1pptx、图形的相似大单元教学设计docx、341相似三角形的判定1docx等3份课件配套教学资源，其中PPT共27页， 欢迎下载使用。
1.经历相似三角形判定定理“平行于三角形一边的直线和其他两边相交，截得的三角形与原三角形相似”的证明过程。2.理解并掌握相似三角形判定定理“平行于三角形一边的直线和其他两边相交，截得的三角形与原三角形相似”。3.能够利用平行线判定三角形相似，并能证明相关结论。4.通过观察、测量、猜想、归纳等过程，体验数学发现的过程和方法。5.培养学生分析问题、解决问题的能力以及逻辑推理能力。
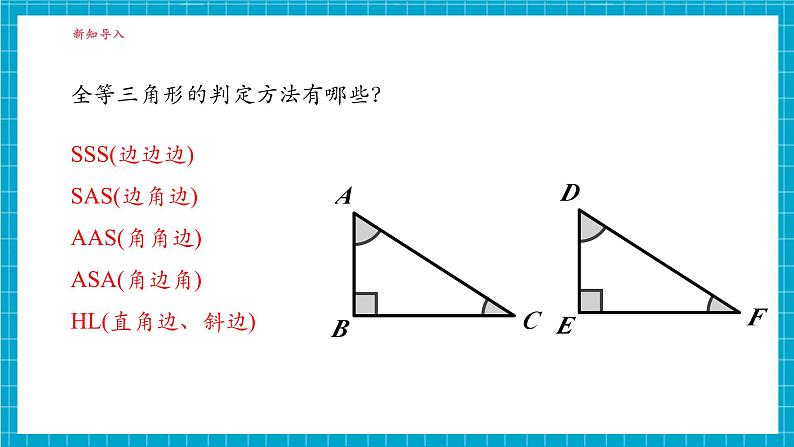
全等三角形的判定方法有哪些？
SSS(边边边)SAS(边角边)AAS(角角边)ASA(角边角)HL(直角边、斜边)
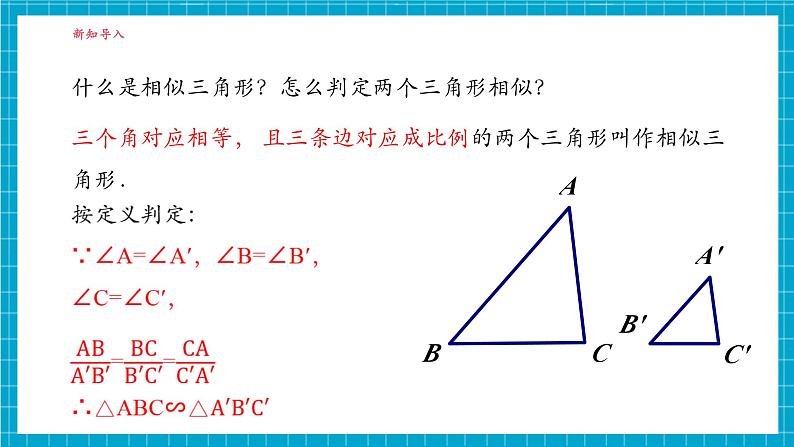
什么是相似三角形？怎么判定两个三角形相似？
三个角对应相等， 且三条边对应成比例的两个三角形叫作相似三角形．
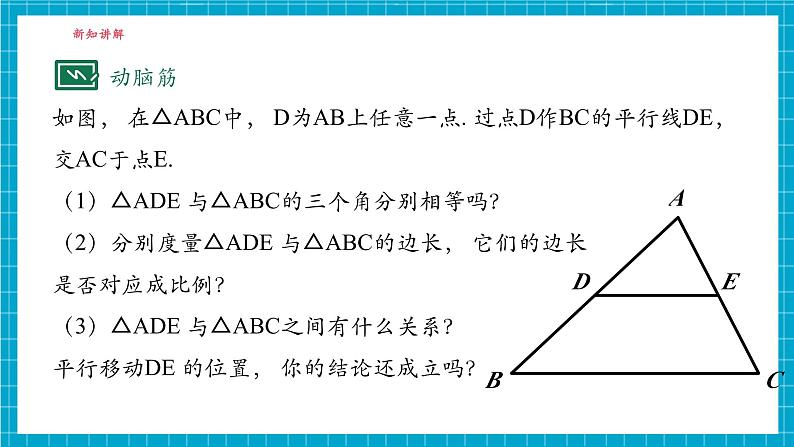
如图， 在△ABC中， D为AB上任意一点. 过点D作BC的平行线DE，交AC于点E.（1）△ADE 与△ABC的三个角分别相等吗？（2）分别度量△ADE 与△ABC的边长， 它们的边长是否对应成比例？（3）△ADE 与△ABC之间有什么关系？ 平行移动DE 的位置， 你的结论还成立吗？
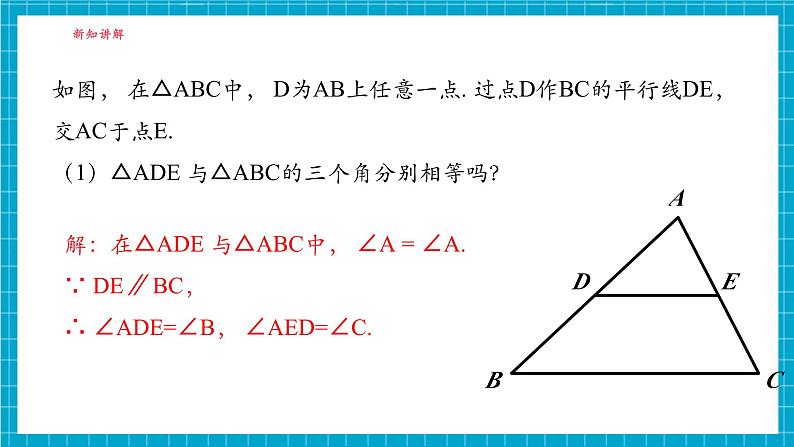
如图， 在△ABC中， D为AB上任意一点. 过点D作BC的平行线DE，交AC于点E.（1）△ADE 与△ABC的三个角分别相等吗？
解：在△ADE 与△ABC中， ∠A = ∠A.∵ DE∥ BC，∴ ∠ADE=∠B， ∠AED=∠C.
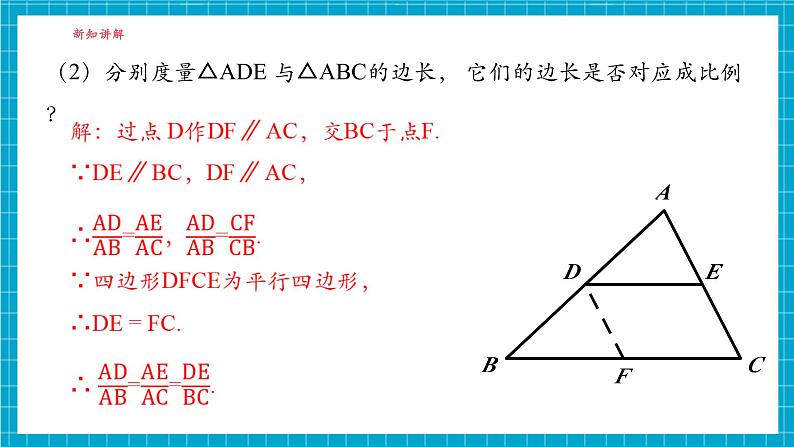
（2）分别度量△ADE 与△ABC的边长， 它们的边长是否对应成比例？
（3）△ADE 与△ABC之间有什么关系？ 平行移动DE 的位置， 你的结论还成立吗？
只要 DE∥ BC， 那么△ADE与△ABC是相似的．
平行于三角形一边的直线与其他两边相交， 截得的三角形与原三角形相似.
几何语言：∵DE∥ BC∴△ADE∽△ABC
如图，在△ABC中，已知点D，E分别是AB，AC边的中点.求证：△ADE∽△ABC.
证明 :∵ 点D,E分别是AB、AC边的中点，∴ DE∥ BC，∴△ADE∽△ABC.
如图，点D为△ABC的边AB的中点，过点D作DE∥ BC，交边AC于点E.延长DE至点F，使DE=EF.求证： △CFE ∽△ABC .
证明 :∵DE∥ BC，点D为△ABC边的中点，∴AE=CE.又DE=FE,∠AED=∠CEF,∴△ADE≌△CFE(SAS).∵DE∥ BC,∴△ADE∽△ABC.∴△CFE ∽△ABC
【知识技能类作业】必做题：
如图，已知点O在四边形ABCD的对角线AC上，OE//CB， OF// CD.试判断四边形AEOF与四边形ABCD是否相似，并说明理由.
平行于三角形一边的直线与其他两边相交， 截得的三角形与原三角形相似.利用平行线判定：∵DE∥ BC∴△ADE∽△ABC
3. 如图，在△ABC中，DE//BC,且DE分别交AB,AC于点D,E,M为边BC上一点，连接AM交DE于点N,则图中相似三角形的组数是( )A.2组B. 3组C.4组D.5组