数学湘教版（2024）4.1 正弦和余弦完整版ppt课件

这是一份数学湘教版（2024）4.1 正弦和余弦完整版ppt课件，文件包含41正弦和余弦1pptx、41正弦和余弦1docx、锐角三角函数大单元设计docx等3份课件配套教学资源，其中PPT共23页， 欢迎下载使用。
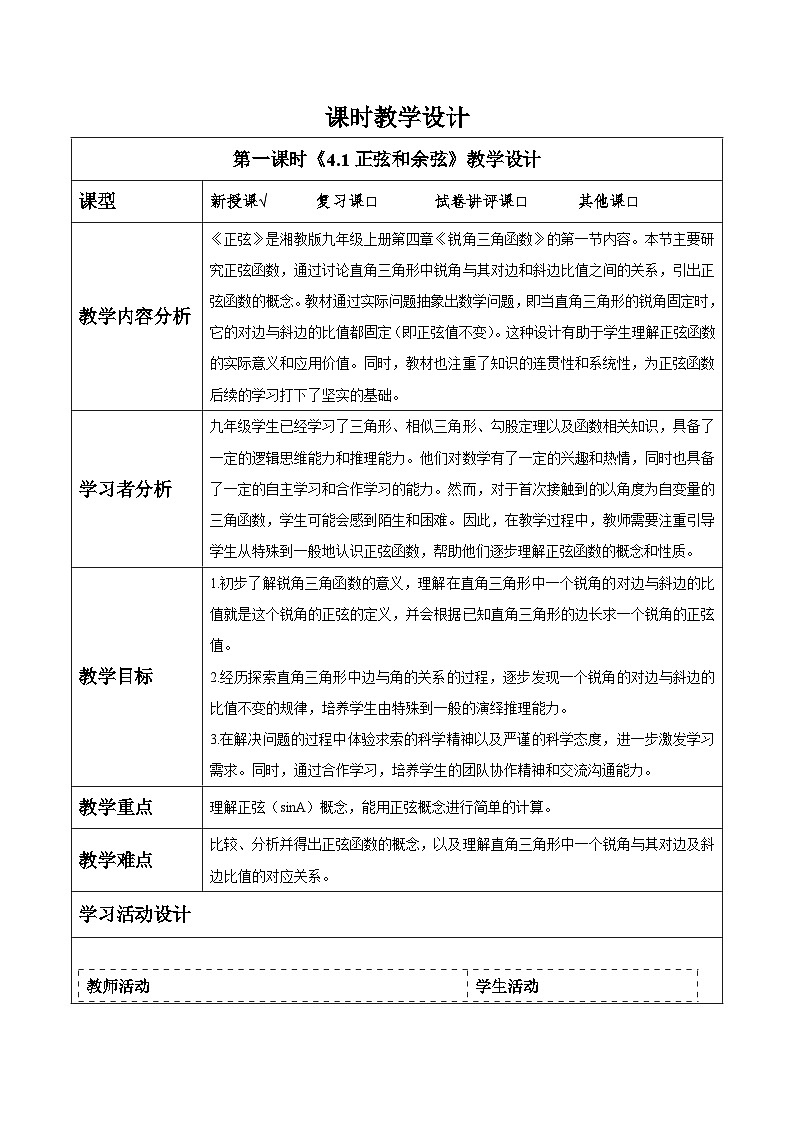
1.初步了解锐角三角函数的意义，理解在直角三角形中一个锐角的对边与斜边的比值就是这个锐角的正弦的定义，并会根据已知直角三角形的边长求一个锐角的正弦值。2.经历探索直角三角形中边与角的关系的过程，逐步发现一个锐角的对边与斜边的比值不变的规律，培养学生由特殊到一般的演绎推理能力。
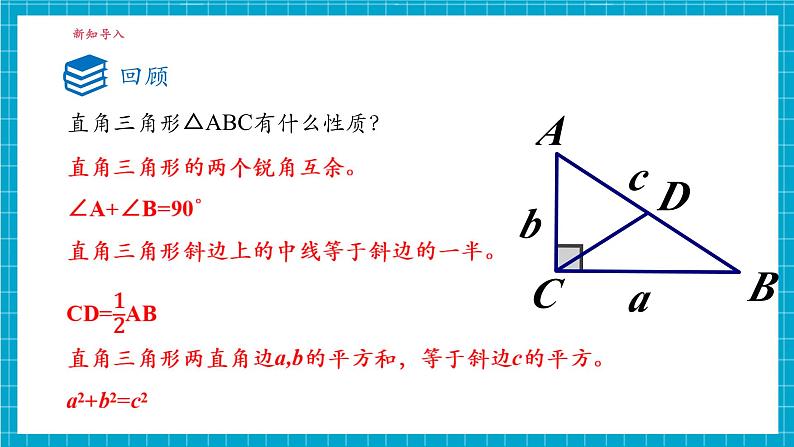
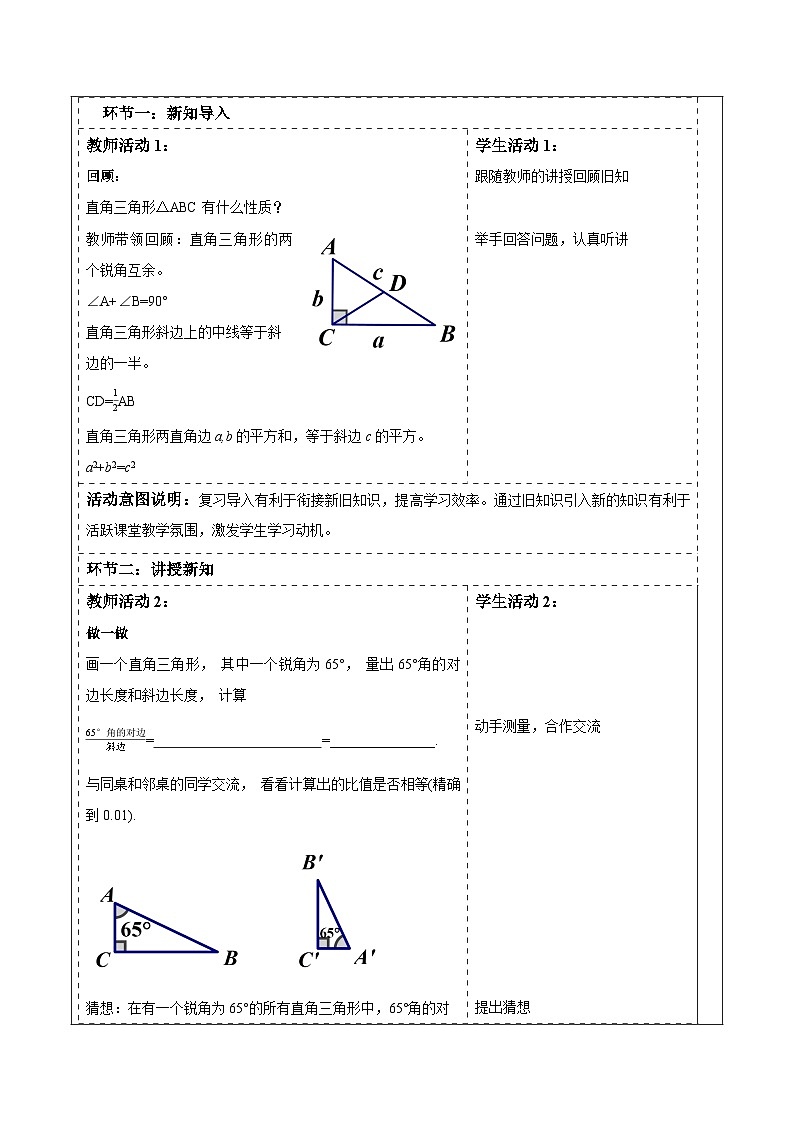
直角三角形△ABC有什么性质？
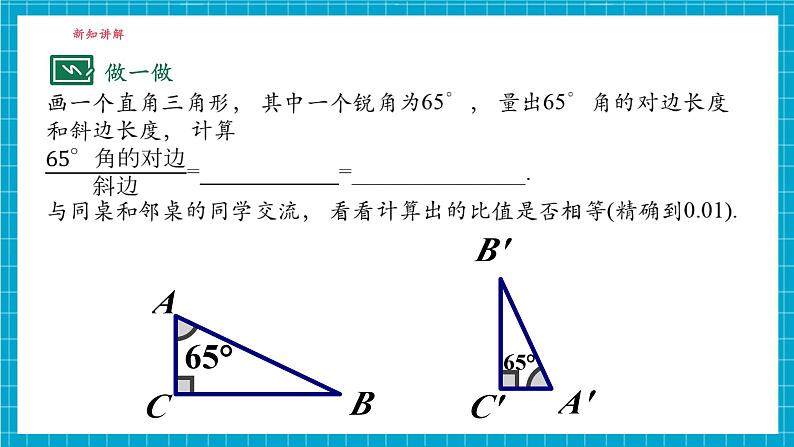
猜想：在有一个锐角为65°的所有直角三角形中，65°角的对边与斜边的比值是一个常数.
思考：若把65°角换成任意一个锐角α， 则这个角的对边与斜边的比值是否也是一个常数呢？
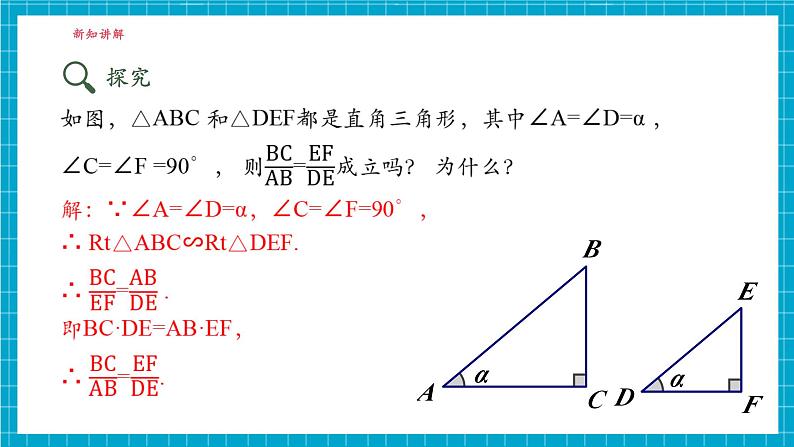
在有一个锐角等于 α 的所有直角三角形中， 角 α 的对边与斜边的比值是一个常数， 与直角三角形的大小无关.
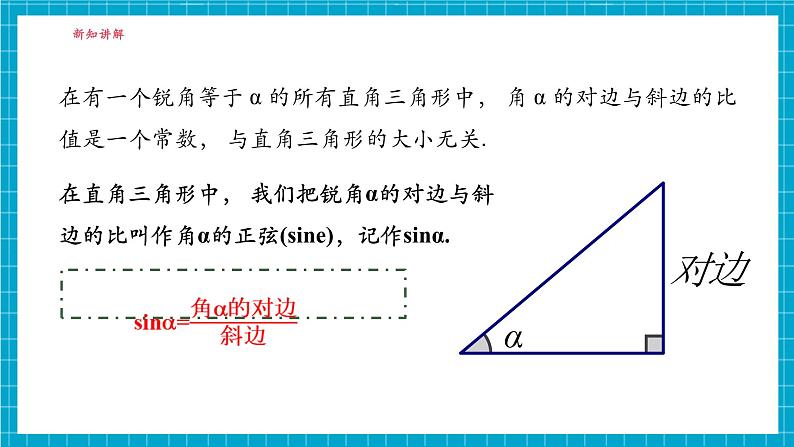
在直角三角形中， 我们把锐角α的对边与斜边的比叫作角α的正弦(sine)，记作sinα.
【知识技能类作业】必做题：
5.计算：sin30°－|－2|＝　 　．6.如图，在△ABC中，DE∥BC，∠B＝30°，则sin∠ADE的值为　 　．
如图所示，在Rt△ABC中，∠ACB＝90°，CD⊥AB，D为垂足，若AC＝4，BC＝3，求sin∠ACD的值．
1.已知Rt△ABC∽Rt△A′B′C′，∠C=∠C′=90°，且AB=2A′B′，则sinA与sinA′的关系为 (　　)A．sinA=2sinA′B．sinA=sinA′　C．2sinA=sinA′　D．不确定
3.在Rt△ABC中，∠B＝90°.若AC＝2BC，则sinC的值是_______.
如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D.(1)求证：△ACD∽△CBD；(2)若AD＝2，AB＝6，求CD的长和sinA的值．
(1)证明：∵∠A＋∠ACD＝90°，∠A＋∠B＝90°，∴∠ACD＝∠B.又∵∠ADC＝∠CDB＝90°，∴△ACD∽△CBD.