湘教版九年级上册3.4 相似三角形的判定与性质精品精练

3.4.2.2 相似三角形的性质2

班级：___________姓名：___________得分：__________

（满分：100分，考试时间：40分钟）

一．选择题（共5小题，每题6分）

1．已知△ABC∽△DEF，相似比为2，且△ABC的周长为16，则△DEF的周长为（　　）

A．2 B．4 C．8 D．32 

2．如果两个相似三角形对应高的比是4：9，那么它们的面积比是（　　）

A．4：9 B．2：3 C．16：81 D．9：4 

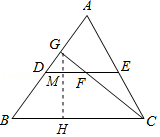
3．如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，若△CEF的面积为18cm2，则S△DGF的值为（　　）

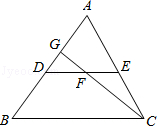
A．4cm2 B．5cm2 C．6cm2 D．7cm2 

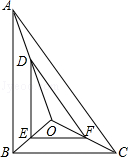
4．如图，在正方形ABCD中，E是BC的中点，F是CD上一点，AE⊥EF，则S△ABE：S△ECF等于（　　）

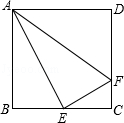
A．1：2 B．4：1 C．2：1 D．1：4 

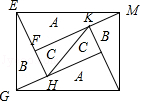
5．如图是一个由A、B、C三种相似的直角三角形纸片拼成的矩形（相似比相同），相邻纸片之间互不重叠也无缝隙，其中A、B、C的纸片的面积分别为S1、S2、S3，若S1＞S2＞S3，则这个矩形的面积一定可以表示为（　　）

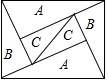
A．4S1 B．6S2 C．4S2+3S3 D．3S1+4S3 

二．填空题（共5小题，每题6分）

6．已知△ABC与△DEF相似，且△ABC与△DEF的相似比为2：3，若△DEF 的面积为36，则△ABC的面积等于　   　．

7．如果两个相似三角形的周长比为2：3，那么这两个相似三角形的面积比为　   　．

8．如果两个相似三角形对应边上的高的比为1：4，那么这两个三角形的周长比是　   　．

9．已知△ABC∽△DEF，且S△ABC=4，S△DEF=9，则=　   　．

10．若△ABC∽△A′B′C′，且△ABC与△A′B′C′的面积之比为1：3，则相似比为　   　．

三．解答题（共3小题，第11、12题每题12分，第13题16分）

11．已知△ABC中．AB=15cm，BC=20cm，AC=25cm，另一个与它相似的△A′B′C′的最长边A′C′=50cm，求△A′B′C′的周长和面积．

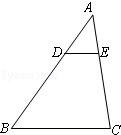
12．如图，△ADE∽△ABC，=，△ABC的面积为18，求四边形BCED的面积．

13．如图，直角三角形ABC到直角三角形DEF是一个相似变换，AC与DF的长度之比是3：2．

（1）DE与AB的长度之比是多少？

（2）已知直角三角形ABC的周长是12cm，面积是6cm2，求直角三角形DEF的周长与面积．

试题解析

一．选择题

1．【分析】根据相似三角形面积的比等于相似比求解即可．

【解答】解：设△DEF的周长为x，

∵△ABC∽△DEF，相似比为2，

∴16：x=2：1，

解得，x=8．

故选：C．

【点评】本题考查了相似三角形的性质，熟记性质是解题的关键．

2．【分析】相似三角形对应高的比等于相似比，再根据相似三角形的面积比等于相似比的平方即可解决问题；

【解答】解：∵两个相似三角形对应高之比为4：9，

∴它们的相似比为4：9，

∴面积比=（）2=16：81．

故选：C．

【点评】本题考查对相似三角形性质的理解．相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方，相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．

3．【分析】作GH⊥BC于H交DE于M，根据三角形中位线定理得到DE∥BC，DE=BC，证明△GDF∽△GBC，根据相似三角形的性质、三角形的面积公式计算．

【解答】解：作GH⊥BC于H交DE于M，

∵DE是△ABC的中位线，

∴DE∥BC，DE=BC，

∵F是DE的中点，

∴DF=BC，

∵DF∥BC，

∴△GDF∽△GBC，

∴==，

∴=，

∵DF=FE，

∴S△DGF=×△CEF的面积=6cm2，

故选：C．

【点评】本题考查的是相似三角形的判定和性质、三角形中位线定理，掌握相似三角形的判定定理和性质定理是解题的关键．

4．【分析】首先根据正方形的性质与同角的余角相等证得：△BAE∽△CEF，再根据相似三角形的性质可得结论．

【解答】解：∵四边形ABCD是正方形，

∴∠B=∠C=90°，AB=BC=CD，

∵AE⊥EF，

∴∠AEF=∠B=90°，

∴∠BAE+∠AEB=90°，∠AEB+∠FEC=90°，

∴∠BAE=∠CEF，

∴△BAE∽△CEF，

∴S△ABE：S△ECF=AB2：CE2，

∵E是BC的中点，

∴BC=2CE=AB

∴==，即S△ABE：S△ECF=4：1

故选：B．

【点评】此题考查了相似三角形的判定与性质，以及正方形的性质，熟练掌握相似三角形面积的比等于相似比的平方．

5．【分析】如图，由A、B、C三种直角三角形相似，设相似比为k，EF=m，则GH=mk，FH=mk2．想办法构建方程，求出k定值，证明S2+S3=S1即可解决问题；

【解答】解：如图，由A、B、C三种直角三角形相似，设相似比为k，EF=m，则GH=mk，FH=mk2．

∴EH=m（1+k2），FM=，FK=km（1+k2），

则有：Km（1+k2）+mk=，

整理得：k4+k2﹣1=0，

∴k2=或（舍弃），

∴S2=S1，S3=（）2S1=S1，

∴S2+S3=S1，

∴这个矩形的面积=2S1+2（S2+S3）=4S1，

故选：A．

【点评】本题考查相似三角形的性质、矩形的性质等知识，解题的关键是学会利用参数，构建方程解决问题，属于中考选择题中的压轴题．

二．填空题

6．【分析】直接利用相似三角形面积比等于相似比的平方得出两三角形面积比，进而得出答案．

【解答】解：∵△ABC～△DEF，相似比为2：3，

∴△ABC的面积与△DEF的面积比为：4：9，

∵△DEF的面积为36

∴△ABC的面积为16，

故答案为16．

【点评】此题主要考查了相似三角形的性质，正确得出三角形的面积比是解题关键．

7．【分析】根据相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方解答．

【解答】解：因为两个相似三角形的周长比为2：3，

所以这两个相似三角形的相似比为2：3，

所以这两个相似三角形的面积比为4：9；

故答案为：4：9．

【点评】本题考查的是相似三角形的性质，相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．

8．【分析】根据相似三角形周长的比、两个相似三角形对应边上的高的比等于相似比解答即可．

【解答】解：∵两个相似三角形对应边上的高的比为1：4，

∴这两个三角形的相似比为1：4，

∴两个相似三角形的周长比为1：4；

故答案为：1：4

【点评】本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比是解题的关键．

9．【分析】直接根据相似三角形的性质即可得出结论．

【解答】解：∵△ABC∽△DEF，且S△ABC=4，S△DEF=9，

∴．

故答案为

【点评】本题考查的是相似三角形的性质，熟知相似三角形的面积的比等于相似比的平方是解答此题的关键．

10．【分析】根据相似三角形面积的比等于相似比的平方解答．

【解答】解：∵△ABC∽△A′B′C′，△ABC与△A′B′C′的面积之比为1：3，

∴△ABC与△A′B′C′的相似比为1：．

故答案为：1：．

【点评】本题考查了相似三角形的性质，是基础题，熟记性质是解题的关键．

三．解答题

11．【分析】根据△ABC中，AB=15cm，BC=20cm，AC=25cm，可得△ABC的周长和面积，利用最长边可求得两三角形的相似比，再根据周长比等于相似比，可求得△A′B′C′的周长，根据相似三角形的面积的比等于相似比的平方，可得△A′B′C′的面积．

【解答】解：∵△ABC中，AB=15cm，BC=20cm，AC=25cm，

∴△ABC的周长=60cm，AB2+BC2=AC2，

∴△ABC是直角三角形，

∴△ABC的面积=×15×20=150cm2，

∵△ABC∽△A′B′C′，且△ABC中最长边为25cm，△A′B′C′的最长边长为50cm，

∴相似比为，

∴=，即=，

解得C△A′B′C′=120cm，

∵=（）2，

∴=，

解得S△A′B′C′=600cm2．

【点评】本题主要考查相似三角形的性质，掌握相似三角形的周长比等于相似比，相似三角形的面积的比等于相似比的平方是解题的关键．

12．【分析】根据题意求出两个三角形的相似比，根据相似三角形的性质得到两个三角形的面积比，求出△ADE的面积，结合图形计算即可．

【解答】解：∵=，

∴=，

∵△ADE∽△ABC，=，

∴△ADE与△ABC的面积比为，又△ABC的面积为18，

∴△ADE的面积为2，

∴四边形BCED的面积=△ABC的面积﹣△ADE的面积=16．

【点评】本题考查的是相似三角形的性质，掌握相似三角形面积的比等于相似比的平方是解题的关键．

13．【分析】根据相似三角形的对应边的比等于相似比，周长比等于相似比，面积比等于相似比的平方解题即可．

【解答】解：（1）由相似变换可得：DE：AB=DF：AC=2：3；

（2）∵AC：DF=3：2，

∴△DEF的周长：△ABC的周长=2：3，

S△DEF：S△ABC=4：9，

∵直角三角形ABC的周长是12cm，面积是6cm2

∴△DEF的周长为8cm，S△DEF=cm2．

【点评】此题主要考查学生对相似三角形的性质的理解及运用．