湘教版九年级上册3.4 相似三角形的判定与性质试讲课教学ppt课件

这是一份湘教版九年级上册3.4 相似三角形的判定与性质试讲课教学ppt课件，文件包含教学课件九上·湘教·341相似三角形的判定第4课时相似三角形的判定定理3pptx、数学九上·湘教·341相似三角形的判定第4课时相似三角形的判定定理3教案docx等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。

3.4.1.4 相似三角形的判定定理3
湘教版数学九年级上册
学习目标
A
B
C
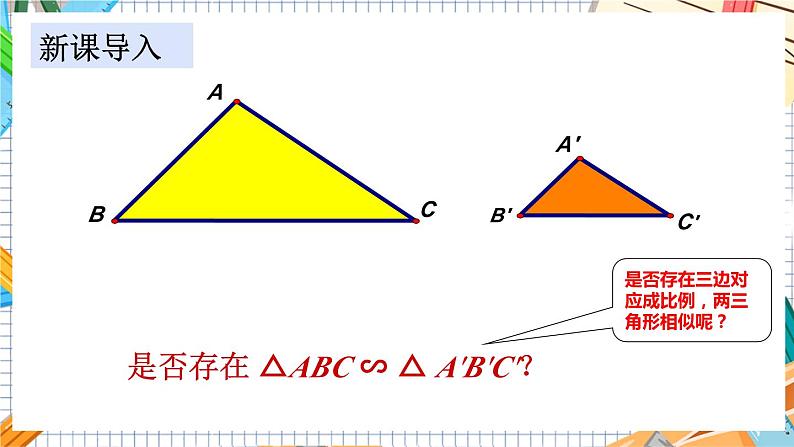
是否存在三边对应成比例，两三角形相似呢？
是否存在 △ABC ∽ △ A'B'C'？
新课导入
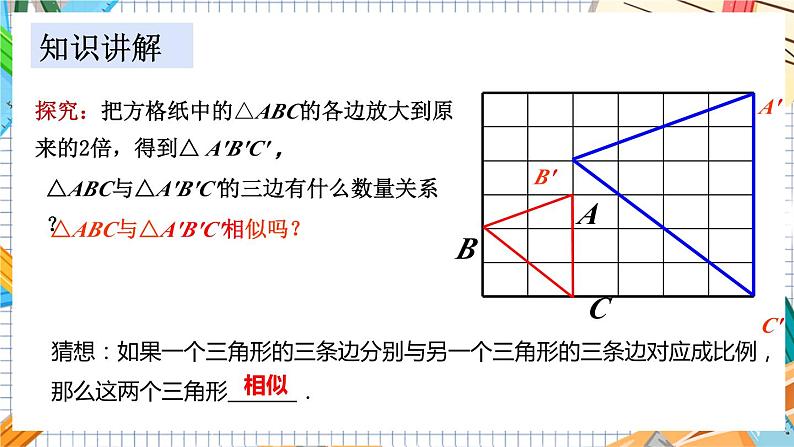
猜想：如果一个三角形的三条边分别与另一个三角形的三条边对应成比例，那么这两个三角形_______．
相似
探究：把方格纸中的△ABC的各边放大到原来的2倍，得到△ A'B'C' ，
△ABC与△A'B'C'相似吗？
△ABC与△A'B'C'的三边有什么数量关系？
知识讲解
思考：如果三角形三条边对应成比例，请验证这两个三角形是相似的.
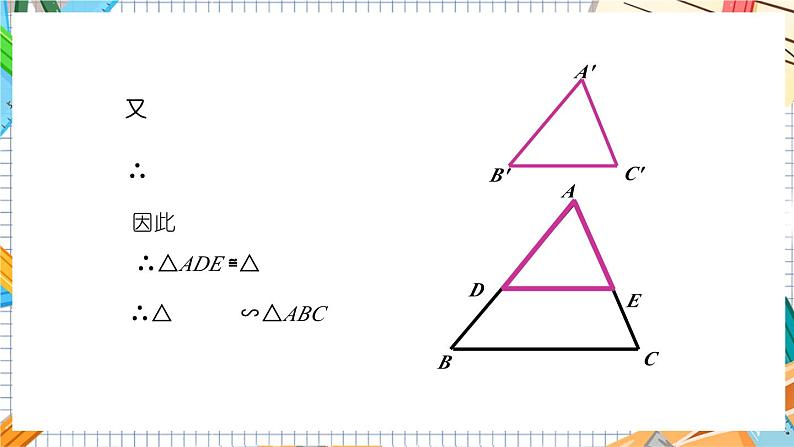
已知:在△ABC 和△A'B'C' 中,
求证:ΔABC ∽ △A'B'C'
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
D
E
过点D作DE∥BC交AC于点E.
∴△ADE∽△ABC，
∵
D
E
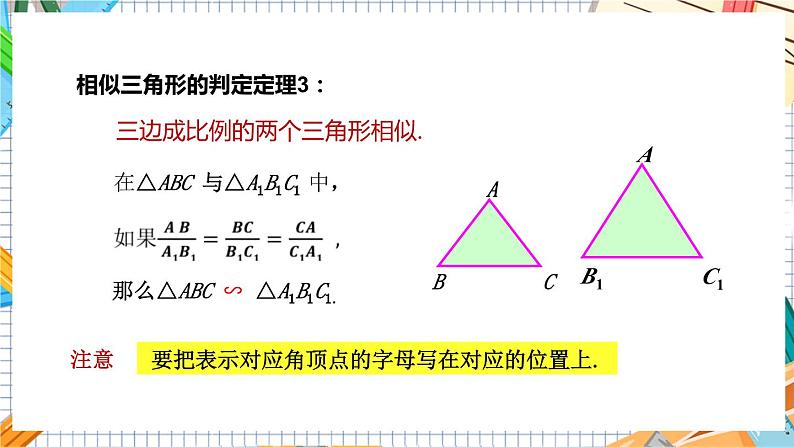
　　三边成比例的两个三角形相似.
那么△ABC ∽ △A1B1C1.
要把表示对应角顶点的字母写在对应的位置上.
注意
在△ABC 与△A1B1C1 中，
相似三角形的判定定理3：
 
已知△ABC和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12， BC=15， AC＝24 DE＝16， EF＝20， DF＝30
(2) AB=4， BC=8， AC＝10 DE＝20， EF＝16， DF＝8
(1) AB=3， BC=4， AC＝6 DE＝6， EF＝8， DF＝9
是
否
否
（大对大，中对中，小对小）
思考：（1）两个直角三角形一定相似吗？ 两个等腰直角三角形呢？为什么？
所有的直角三角形不都相似；所有的等腰直角三角形都相似.
（2）两个等腰三角形一定相似吗？ 两个等边三角形呢？为什么？
所有的等腰三角形不都相似；所有的等边三角形都相似.
分析: 已知两边成比例，只要得到三边成比例，即可完成证明.
∴
Rt△ABC∽
Rt△
（三边成比例的两个三角形相似）
例8 判断下图中的两个三角形是否相似，并说明理由.
∴ △DEF∽△ABC.
1.　如图 所示，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与图中△ ABC 相似的是（　　）
B
随堂训练
2. 如图所示，在正方形网格中有5个三角形：①，②，③，④，⑤,在②～⑤中，与①相似的是(　　)A.②③④ 　B.③④⑤ 　　C.②④⑤ 　D.②③⑤
B
 
解析:
 
∴ΔABC∽ΔADE，∴∠BAC=∠DAE，∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE.
 
∵
证明：
解:相似相似比为2:1.
 
　　两边成比例且夹角相等的两个三角形相似.
相似三角形的判定定理2：
相似三角形的判定定理1：
　　两角分别相等的两个三角形相似.
相似三角形的判定：
平行于三角形一边的直线与其他两边相交，截得的三角形与原三角形相似．
　　三边成比例的两个三角形相似.
相似三角形的判定定理3：
课堂小结