湘教版数学九上 4.1 第1课时 正弦 课件

这是一份湘教版数学九上 4.1 第1课时 正弦 课件，共12页。

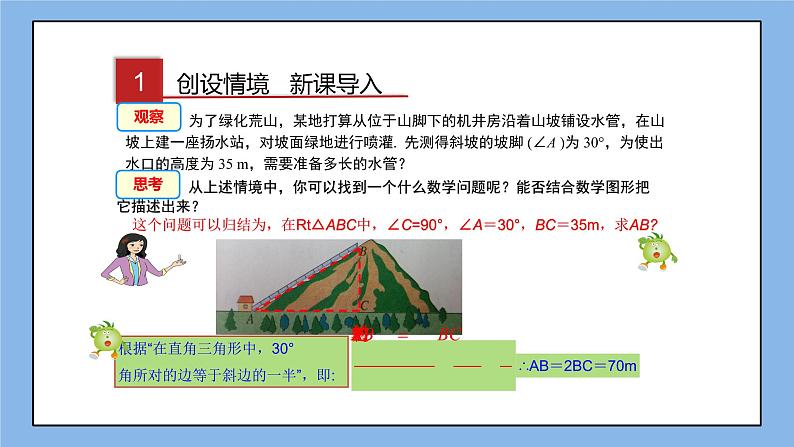
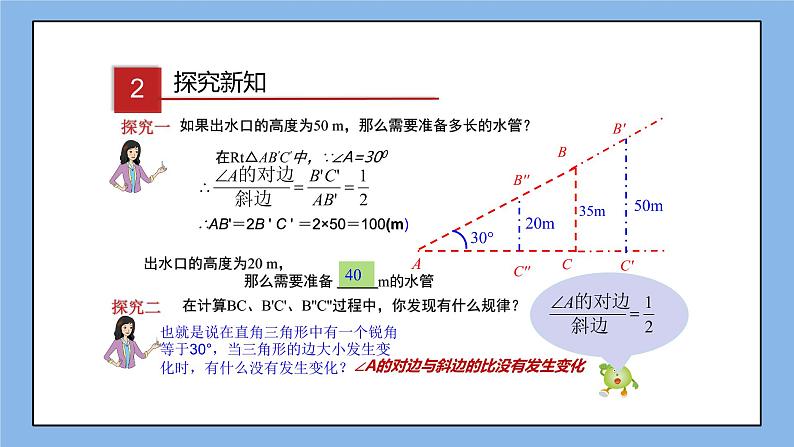
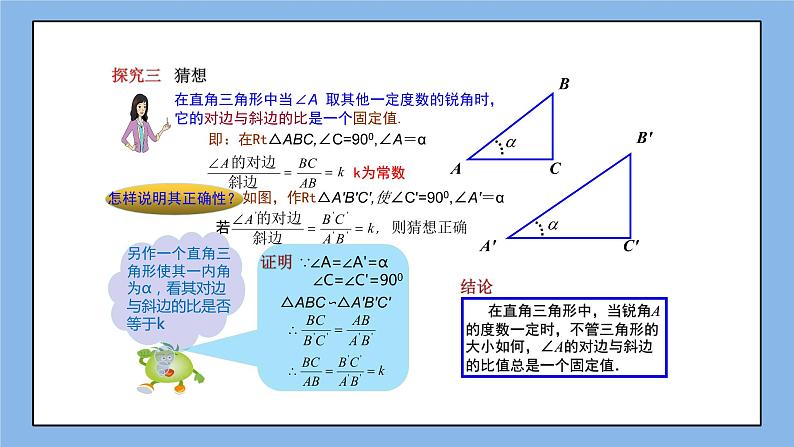
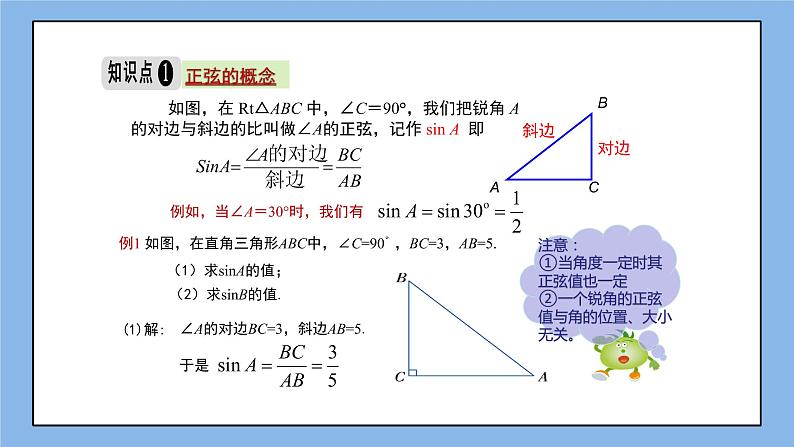
第1课时 正 弦 4.1 正弦和余弦第4章 锐角三角函数 从上述情境中，你可以找到一个什么数学问题呢？能否结合数学图形把它描述出来？ABC35m? 为了绿化荒山，某地打算从位于山脚下的机井房沿着山坡铺设水管，在山坡上建一座扬水站，对坡面绿地进行喷灌. 先测得斜坡的坡脚 (∠A )为 30°，为使出水口的高度为 35 m，需要准备多长的水管？观察思考这个问题可以归结为，在Rt△ABC中，∠C=90°，∠A＝30°，BC＝35m，求AB?根据“在直角三角形中，30°角所对的边等于斜边的一半”，即:∴AB＝2BC＝70m∴AB＝2BC＝70m探究一如果出水口的高度为50 m，那么需要准备多长的水管？B'C'50m在Rt△AB'C'中，∵∠A=300∴AB'＝2B ' C ' ＝2×50＝100(m)出水口的高度为20 m， 那么需要准备 m的水管20mB''C''40探究二35m在计算BC、B'C'、B''C''过程中，你发现有什么规律？也就是说在直角三角形中有一个锐角等于30°，当三角形的边大小发生变化时，有什么没有发生变化？∠A的对边与斜边的比没有发生变化在直角三角形中当∠A 取其他一定度数的锐角时，它的对边与斜边的比是一个固定值.探究三猜想如图，作Rt△A'B'C',使∠C'=900,∠A'＝α 在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比值总是一个固定值．结论证明即：在Rt△ABC,∠C=900,∠A＝α △ABC∽△A'B'C'∵∠A=∠A'=ɑ ∠C=∠C'=900k为常数正弦的概念 如图，在 Rt△ABC 中，∠C＝90°，我们把锐角 A 的对边与斜边的比叫做∠A的正弦，记作 sin A 即例如，当∠A＝30°时，我们有对边斜边例1 如图，在直角三角形ABC中，∠C=90°，BC=3，AB=5.（1）求sinA的值；（2）求sinB的值.(1)解:∠A的对边BC=3，斜边AB=5.于是2、在直角三角形ABC中，∠C=90°， BC=5，AB=13.则sinB=（ ） (2)解:∠B的对边是AC，根据勾股定理，得 AC2 = AB2-BC2 = 52-32 = 16于是 AC = 4因此方法总结：正确理解锐角的正弦的概念 1、 在 Rt△ABC中，锐角 A 的对边和斜边同时扩大 100 倍，sinA 的值 ( ) A. 扩大100倍 B. 缩小100倍 C. 不变 D. 不能确定练一练 C知识点❶利用正弦定义求正弦值 例2、如图， 在平面直角坐标系内有一点P（3，4）， 连接OP， 求OP与x轴正方向所夹锐角α 的正弦值.解： 平面直角坐标系内点P的坐标为（3，4）， 连接OP，由勾股定理得 OP=5, 角α的对边是直角边，边长为4，而斜边长OP为5 ， ∴知识点❷求网格中锐角的正弦值例3、如图，△ABC的顶点都在正方形方格纸的格点上，则SinA=方法总结：构造直角三角形，利用正弦的定义求解练习1、如图，△ABC的顶点都在正方形方格纸的格点上，则SinB=（ ）2、如图，△ABC的顶点都在正方形方格纸的格点上，则SinC=（ ）知识点❸利用正弦值求三角形边长和面积例4、如图，在△ABC中，AB=AC=13，sinB= ,求△ABC的面积CABD解析：要求△ABC就要知道底与高，根据正弦的定义要构造直角三角形，由等腰三角形三线合因此作底边上的高AD，就可求出BC和高AD，从而求面积。解：作AD┴BD于D，∵AB=AC∴BC=2BD∵在Rt△ABD中，sinB= AB=AC=13∴AD=5∴在Rt△ABD中，AB2=BD2+AD2132=BD2+52∴BD=12BC=2BD=24知识点❹利用参数法求锐角的正弦例5、如图在Rt△ABC中，∠C＝90°，sinA= 求∠B的正弦解析：要求∠B的正弦正弦必须知道三边的长。因知道sinA= ,因此若设BC=2k,则AB=3k,则勾股定理求出AC关于k的式子，从而求出sinB.解:∵∠C＝90° ∴ sinA=设BC=2k,则AB=3k由勾股定理AC2+BC2=AB2AC2+（2k)2=(3k)2∴ AC=故sinB=练一练：如图在Rt△ABC中，∠C＝90°，M为BC边的中点，sin∠CAM=则sinB=( ) 正 弦正弦的应用正弦的概念已知边长求正弦值已知正弦值求边长1. 在直角t△ABC 中，若三边长都扩大 2 倍，则锐角 A 的正弦值( ) A. 扩大 2 倍 B.不变 C. 缩小 D. 无法确定5布置作业3. 如图，在正方形网格中有 △ABC，则 sin∠ABC的值为 .4. 如图，在 △ABC 中， AB = BC = 5，sinA = ，求 △ABC 的面积.