资料中包含下列文件,点击文件名可预览资料内容










还剩10页未读,
继续阅读
所属成套资源:湘教版数学九年级上学期PPT课件+教案全套
成套系列资料,整套一键下载
数学九上·湘教·4.1正弦和余弦(第3课时余弦) 教学课件+教案
展开
这是一份数学九上·湘教·4.1正弦和余弦(第3课时余弦) 教学课件+教案,文件包含教学课件九上·湘教·41正弦和余弦第3课时余弦pptx、数学九上·湘教·41正弦和余弦第3课时余弦教案docx等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
4.1.3 余弦
湘教版数学九年级上册
1
2
会求特殊角的余弦值并熟记这些值.(难点)
会利用相似直角三角形,探索并认识余弦.(重点)
会用计算器求锐角的余弦值及已知余弦值求对应的锐角.(难点)
3
学习目标
1.什么是锐角α的正弦?2.下列特殊角的正弦值分别是什么?
在直角三角形中, 我们把锐角α的对边与斜边的比叫作角α的正弦,记作sinα
新课导入
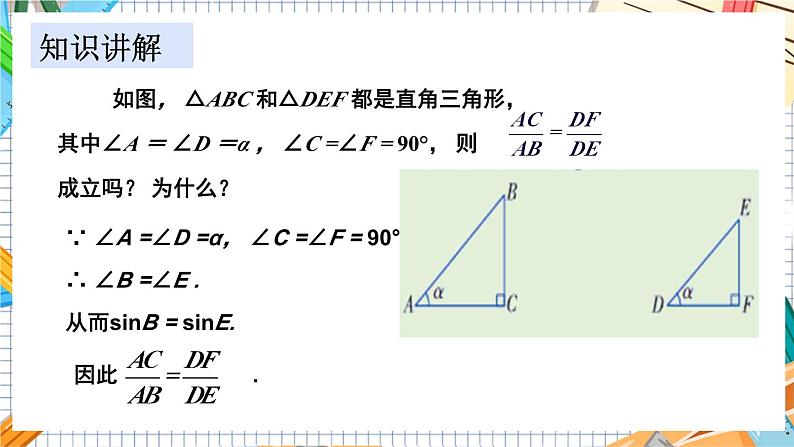
如图, △ABC 和△DEF 都是直角三角形, 其中∠A = ∠D =α , ∠C =∠F = 90°, 则成立吗? 为什么?
∵ ∠A =∠D =α, ∠C =∠F = 90°,∴ ∠B =∠E .从而sinB = sinE.
因此 .
知识讲解
定义 在直角三角形中,锐角α的邻边与斜边的比叫作角α的余弦,记作 cosα,即
如图,在直角三角形ABC中,∠C=90°,∠A,∠B,∠C的对边分别记作a,b,c . ∠A的正弦值是什么?∠B的余弦值呢?它们相等吗?
从上述探究和证明过程看出,对于任意锐角α,有
探究结论
cosα = sin(90°- α),
sinα = cos(90°- α).
例1 求cos30°, cos45°, cos60°的值.
解:
练一练:
通过前面的学习,我们已经知道了三个特殊角(30°, 45°, 60°)的余弦值, 而对于一般锐角α 的余弦值, 仍可以利用计算器来求.
例如求50°角的余弦值, 可以在计算器上依次按键cos 50 ,显示结果为0.64627 …,
练一练:利用计算器计算:(1) cos 15°≈ (精确到0.0001);(2) cos 50° 48 ′≈ (精确到0.0001);(3) 若cos α = 0.965 9, 则α ≈ (精确到0.1°);(4) 若cos α = 0.258 8, 则α ≈ (精确到0.1°).
答案:(1)0.965 9;
(2)0.632 0;
(3)15.0 °;
(4)75.0 °.
例2 计算:
= ,
1.如图,在Rt△ABC中,∠C=90°,AB=6, cosB= ,则BC的长为( )
A
A.4 B.2 C. D.
随堂训练
2.计算:
(1)sin30°+cos45°;(2)sin260°+ cos260°- 2sin30°.
解:(1)sin30°+cos45°
(2) sin260°+cos260°- 2sin30°
知识讲解
变形应用:
课堂小结
4.1.3 余弦
湘教版数学九年级上册
1
2
会求特殊角的余弦值并熟记这些值.(难点)
会利用相似直角三角形,探索并认识余弦.(重点)
会用计算器求锐角的余弦值及已知余弦值求对应的锐角.(难点)
3
学习目标
1.什么是锐角α的正弦?2.下列特殊角的正弦值分别是什么?
在直角三角形中, 我们把锐角α的对边与斜边的比叫作角α的正弦,记作sinα
新课导入
如图, △ABC 和△DEF 都是直角三角形, 其中∠A = ∠D =α , ∠C =∠F = 90°, 则成立吗? 为什么?
∵ ∠A =∠D =α, ∠C =∠F = 90°,∴ ∠B =∠E .从而sinB = sinE.
因此 .
知识讲解
定义 在直角三角形中,锐角α的邻边与斜边的比叫作角α的余弦,记作 cosα,即
如图,在直角三角形ABC中,∠C=90°,∠A,∠B,∠C的对边分别记作a,b,c . ∠A的正弦值是什么?∠B的余弦值呢?它们相等吗?
从上述探究和证明过程看出,对于任意锐角α,有
探究结论
cosα = sin(90°- α),
sinα = cos(90°- α).
例1 求cos30°, cos45°, cos60°的值.
解:
练一练:
通过前面的学习,我们已经知道了三个特殊角(30°, 45°, 60°)的余弦值, 而对于一般锐角α 的余弦值, 仍可以利用计算器来求.
例如求50°角的余弦值, 可以在计算器上依次按键cos 50 ,显示结果为0.64627 …,
练一练:利用计算器计算:(1) cos 15°≈ (精确到0.0001);(2) cos 50° 48 ′≈ (精确到0.0001);(3) 若cos α = 0.965 9, 则α ≈ (精确到0.1°);(4) 若cos α = 0.258 8, 则α ≈ (精确到0.1°).
答案:(1)0.965 9;
(2)0.632 0;
(3)15.0 °;
(4)75.0 °.
例2 计算:
= ,
1.如图,在Rt△ABC中,∠C=90°,AB=6, cosB= ,则BC的长为( )
A
A.4 B.2 C. D.
随堂训练
2.计算:
(1)sin30°+cos45°;(2)sin260°+ cos260°- 2sin30°.
解:(1)sin30°+cos45°
(2) sin260°+cos260°- 2sin30°
知识讲解
变形应用:
课堂小结
相关资料
更多









