中考数学一轮复习专题18 解直角三角形（10个高频考点）（强化训练）（2份，原卷版+解析版）

这是一份中考数学一轮复习专题18 解直角三角形（10个高频考点）（强化训练）（2份，原卷版+解析版），文件包含中考数学一轮复习专题18解直角三角形10个高频考点强化训练原卷版doc、中考数学一轮复习专题18解直角三角形10个高频考点强化训练解析版doc等2份试卷配套教学资源，其中试卷共81页， 欢迎下载使用。
【考点1 锐角三角函数的定义】
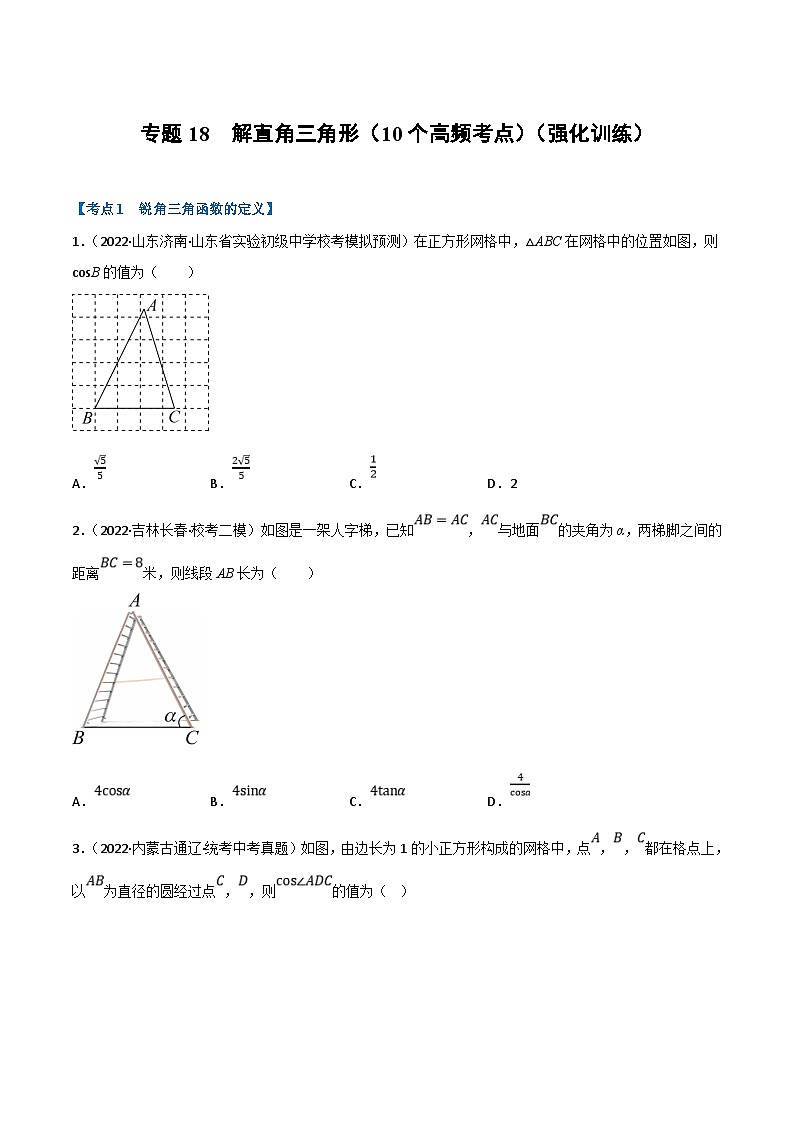
1．（2022·山东济南·山东省实验初级中学校考模拟预测）在正方形网格中，△ABC在网格中的位置如图，则csB的值为（ ）
A．B．C．D．2
2．（2022·吉林长春·校考二模）如图是一架人字梯，已知，与地面的夹角为α，两梯脚之间的距离米，则线段AB长为（ ）
A．B．C．D．
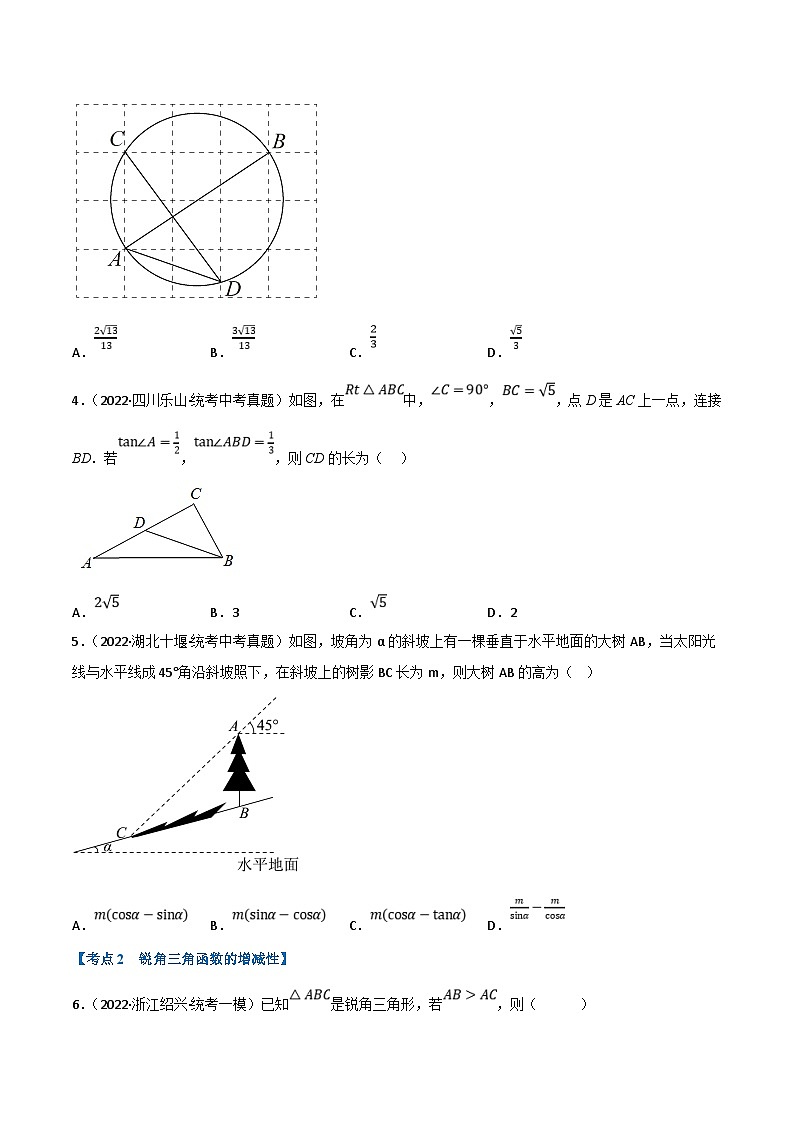
3．（2022·内蒙古通辽·统考中考真题）如图，由边长为1的小正方形构成的网格中，点，，都在格点上，以为直径的圆经过点，，则的值为（ ）
A．B．C．D．
4．（2022·四川乐山·统考中考真题）如图，在中，，，点D是AC上一点，连接BD．若，，则CD的长为（ ）
A．B．3C．D．2
5．（2022·湖北十堰·统考中考真题）如图，坡角为α的斜坡上有一棵垂直于水平地面的大树AB，当太阳光线与水平线成45°角沿斜坡照下，在斜坡上的树影BC长为m，则大树AB的高为（ ）
A．B．C．D．
【考点2 锐角三角函数的增减性】
6．（2022·浙江绍兴·统考一模）已知是锐角三角形，若，则（ ）
A．B．C．D．
7．（2022·浙江金华·校联考一模）若∠A是锐角，且sinA＝，则（ ）
A．0°＜∠A＜30°B．30°＜∠A＜45°C．45°＜∠A＜60°D．60°＜∠A＜90°
8．（2022·山东临沂·统考一模）如图，撬钉子的工具是一个杠杆，动力臂，阻力臂，如果动力F的用力方向始终保持竖直向下，当阻力不变时，则杠杆向下运动时的动力变化情况是（ ）
A．越来越小B．不变C．越来越大D．无法确定
9．（2022·浙江宁波·统考一模）红领巾的形状是等腰三角形，底边长为100厘米，腰长为60厘米，则底角（ ）
A．小于30°B．大于30°且小于45°C．等于30°D．大于45°且小于60°
10．（2022·四川成都·统考一模）已知＜csA＜sin70°，则锐角A的取值范围是_________
【考点3 同角三角函数的关系】
11．（2022·陕西西安·交大附中分校校考模拟预测）已知为锐角， ，求的值．
12．（2022·广东·九年级统考竞赛）现有如下信息：（1）黄金分割比（简称：黄金比）是指把一条线段分割为两部分，较短部分与较长部分的长度之比等于较长部分与整体长度之比，其比值为；（2）黄金三角形被誉为最美三角形，是较短边与较长边之比为黄金比的等腰三角形；（3）有一个内角为的等腰三角形为黄金三角形．由上述信息可求得______．
13．（2022·陕西西安·交大附中分校校考模拟预测）已知，都是锐角，且，，则________．
14．（2022·陕西西安·交大附中分校校考模拟预测）化简：（其中）=___________．
15．（2022秋·安徽亳州·九年级统考期末）如图，在△ABC中，∠C＝90°，a，b，c分别∠A，∠B，∠C的对边．
(1)求的值；
(2)填空：当为锐角时，______；
(3)利用上述规律，求下列式子的值：．
【考点4 互余两角三角函数的关系】
16．（2022·浙江杭州·统考二模）在Rt中，，，则______．
17．（2022·浙江杭州·模拟预测）如图，在Rt△ABC中，∠A=90°，AD⊥BC，垂足为D．给出下列四个结论：①sinα=sinB；②sinβ=sinC；③sinB=csC；④sinα=csβ.其中正确的结论有_____.
18．（2022·四川内江·统考一模）在△ABC中，已知∠C=90°，，则 =___．
19．（2012·湖南衡阳·中考真题）观察下列等式
①sin30°=cs60°=
②sin45°=cs=45°=
③sin60°=cs30°=
…
根据上述规律，计算sin2a+sin2（90°﹣a）= ．
20．（2022·湖南娄底·统考中考真题）高速公路上有一种标线叫纵向减速标线，外号叫鱼骨线，作用是为了提醒驾驶员在开车时减速慢行．如图，用平行四边形表示一个“鱼骨”，平行于车辆前行方向，，过B作的垂线，垂足为（A点的视觉错觉点），若，则________．
【考点5 特殊角的三角函数】
21．（2022·黑龙江绥化·统考中考真题）定义一种运算；，．例如：当，时， ，则的值为_______．
22．（2022·浙江杭州·杭州绿城育华学校校考模拟预测）已知为锐角，若，则的度数为______ ．
23．（2022·四川自贡·校考一模）在中，若，，都是锐角，则是______三角形．
24．（2022·辽宁丹东·统考一模）在平面直角坐标系中，已知点，，点是轴上的一个动点，当时，点的坐标为________．
25．（2022·上海静安·统考一模）计算：．
【考点6 解直角三角形】
26.（2022·江苏无锡·无锡市天一实验学校校考模拟预测）如图，中，分别以、为底边向外作等腰和等腰，连接，点为的中点，连接并延长交的延长线于点，，，若，，则的值为______．
27.（2022·辽宁丹东·统考中考真题）如图，AB是⊙O的直径，点E在⊙O上，连接AE和BE，BC平分∠ABE交⊙O于点C，过点C作CD⊥BE，交BE的延长线于点D，连接CE．
(1)请判断直线CD与⊙O的位置关系，并说明理由；
(2)若sin∠ECD＝，CE＝5，求⊙O的半径．
28.（2022·上海·统考中考真题）一个一次函数的截距为1，且经过点A（2，3）．
(1)求这个一次函数的解析式；
(2)点A，B在某个反比例函数上，点B横坐标为6，将点B向上平移2个单位得到点C，求cs∠ABC的值．
29.（2022·山东烟台·统考中考真题）
(1)【问题呈现】如图1，△ABC和△ADE都是等边三角形，连接BD，CE．求证：BD＝CE．
(2)【类比探究】如图2，△ABC和△ADE都是等腰直角三角形，∠ABC＝∠ADE＝90°．连接BD，CE．请直接写出的值．
(3)【拓展提升】如图3，△ABC和△ADE都是直角三角形，∠ABC＝∠ADE＝90°，且＝＝．连接BD，CE．
①求的值；
②延长CE交BD于点F，交AB于点G．求sin∠BFC的值．
30.（2023·上海静安·统考一模）如图，已知在中，为锐角，是边上的高，， ．
(1)求的长；
(2)求的正弦值．
【考点7 解直角三角形的应用之仰角俯角问题】
31．（2022·湖北黄石·统考中考真题）某校数学兴趣小组开展无人机测旗杆的活动：已知无人机的飞行高度为30m，当无人机飞行至A处时，观测旗杆顶部的俯角为30°，继续飞行20m到达B处，测得旗杆顶部的俯角为60°，则旗杆的高度约为________m．（参考数据：，结果按四舍五八保留一位小数）
32．（2022·贵州黔东南·统考中考真题）如图，校园内有一株枯死的大树，距树12米处有一栋教学楼，为了安全，学校决定砍伐该树，站在楼顶处，测得点的仰角为45°，点的俯角为30°，小青计算后得到如下结论：①米；②米；③若直接从点处砍伐，树干倒向教学楼方向会对教学楼有影响；④若第一次在距点的8米处的树干上砍伐，不会对教学楼造成危害.其中正确的是_______．（填写序号，参考数值：，）
33．（2022·海南·统考中考真题）无人机在实际生活中应用广泛．如图8所示，小明利用无人机测量大楼的高度，无人机在空中P处，测得楼楼顶D处的俯角为，测得楼楼顶A处的俯角为．已知楼和楼之间的距离为100米，楼的高度为10米，从楼的A处测得楼的D处的仰角为（点A、B、C、D、P在同一平面内）．
(1)填空：___________度，___________度；
(2)求楼的高度（结果保留根号）；
(3)求此时无人机距离地面的高度．
34．（2022·内蒙古呼和浩特·统考中考真题）“一去紫台连朔漠，独留青冢向黄昏”，美丽的昭君博物院作为著名景区现已成为外地游客到呼和浩特市旅游的打卡地．如图，为测量景区中一座雕像的高度，某数学兴趣小组在处用测角仪测得雕像顶部的仰角为，测得底部的俯角为．已知测角仪与水平地面垂直且高度为1米，求雕像的高．（用非特殊角的三角函数及根式表示即可）
35．（2022·四川宜宾·统考中考真题）宜宾东楼始建于唐代，重建于宜宾建城2200周年之际的2018年，新建成的东楼（如图1）成为长江首城会客厅、旅游休闲目的地、文化地标打卡地．某数学小组为测量东楼的高度，在梯步A处（如图2）测得楼顶D的仰角为45°，沿坡比为7：24的斜坡AB前行25米到达平台B处，测得楼顶D的仰角为60°，求东楼的高度DE．（结果精确到1米．参考数据：，）
【考点8 解直角三角形的应用之方位角问题】
36．（2022·辽宁葫芦岛·统考一模）如图为某景区五个景点A，B，C，D，E的平面示意图，B在A的正东方向，D在A的北偏东方向上，与A相距300米，E在D的正东方向140米处，C在A的北偏东方向上，C，E均在B的正北方向．
(1)求景点B，E之间的距离；
(2)求景点A，C之间的距离．（结果保留根号）
37．（2022·重庆·统考二模）一天，爸爸带着他的一儿一女去海边玩，爸爸和哥哥在距海岸线（抽象为直线l）一定距离的A处休息，妹妹带上游泳圈在距海岸线40米的B处游泳．过了一会儿，海浪逐渐变大，妹妹由于过度紧张，无法继续游动，只好在B处呼救，爸爸和哥哥听到妹妹呼救，立刻起身．情急之下，哥哥沿AB方向奔跑，由E处下海，沿EB游向妹妹；爸爸沿AD方向奔跑，由D处下海，再沿DB游向妹妹．如图所示，BD⊥l于点D，点B在点A北偏西37°方向，点D在点A北偏西60°方向，A、E、B三点共线．（参考数据：sin37°≈0.6，cs37°≈0.8，tan37°≈0.75，1.73）
(1)求点A到海岸线的距离（结果精确到0.1米）；
(2)若爸爸和哥哥在沙滩上奔跑的速度均为2m/s，在水中游泳的速度均为0.5m/s，请用数据说明，爸爸和哥哥谁先到达妹妹身边？
38．（2022·重庆·西南大学附中校考三模）北京冬奥会的成功举办，点燃了小明和小代的健身热情，两人立即制定好计划积极投入到健身中，如图，小明家住在A地，小代家住在B地，健身馆在C地，在A处测得健身馆C在A的北偏东15方向上，在B处测得健身馆C在B的北偏西45方向上，B在A的北偏东60方向上．某天小明和小代分别从自己家出发到C地健身，他们约定先在AC上的D处汇合，小明沿着AC方慢跑，小代沿着正西方向以180m/min的速度跑了5分钟到D．（参考数据：，，）
(1)求小明家A到小代家B的距离；（结果精确到0.1m）
(2)他们在D处汇合的时间恰好为13：57，若他们要在预定的14：00到达健身馆C，请问他们汇合之后的速度至少应为多少？
39．（2022·湖南怀化·统考模拟预测）某地修建了一座以“讲好隆平故事，厚植种子情怀”为主题的半径为800米的圆形纪念园．如图，纪念园中心点A位于C村西南方向和B村南偏东60°方向上，C村在B村的正东方向且两村相距2.4千米．有关部门计划在B、C两村之间修一条笔直的公路来连接两村．问该公路是否穿过纪念园？试通过计算加以说明． （参考数据：≈1.73，≈1.41）
40．（2022·四川达州·统考一模）深圳是沿海城市，每年都会受到几次台风侵袭，台风是一种自然灾害，它以台风中心为圆心在数十千米范围内形成气旋风景，有极强的破坏力．某次，据气象观察，距深圳正南200千米的处有一台风中心，中心最大风力为12级，每远离台风中心30千米，风力就会减弱一级，该台风中心正以20千米/时的速度沿北偏东43°方向向移动，且台风中心风力不变，若城市受到风力达到或超过六级，则称受台风影响．
（1）此次台风会不会影响深圳？为什么？
（2）若受到影响，那么受到台风影响的最大风力为几级？
（3）若受到影响，那么此次台风影响深圳共持续多长时间？（结果可带根号表示）（sin43°≈，cs42°≈，tan42°≈）
【考点9 解直角三角形的应用之坡度坡比问题】
41．（2022·贵州毕节·统考中考真题）如图，某地修建一座高的天桥，已知天桥斜面的坡度为，则斜坡的长度为（ ）
A．B．C．D．
42．（2022·山东济南·统考一模）如图，为了测量某建筑物 的高度，小颖采用了如下的方法：先从与建筑物底端B在同一水平线上的A点出发，沿斜坡行走100米至坡顶D处，再从D处沿水平方向继续前行若干米到点E处，在E点测得该建筑物顶端C的仰角为59°，建筑物底端B的俯角为，点A、B、C、D、E在同一平面内，斜坡的坡度 ．根据以上数据，计算出建筑物BC的高度约为（结果精确到1．参考数据：，，）（ ）
A．158米B．161米C．159米D．160米
43．（2022·内蒙古·中考真题）在一次综合实践活动中，某小组对一建筑物进行测量．如图，在山坡坡脚C处测得该建筑物顶端B的仰角为60°，沿山坡向上走20m到达D处，测得建筑物顶端B的仰角为30°．已知山坡坡度，即，请你帮助该小组计算建筑物的高度．（结果精确到0.1m，参考数据：）
44．（2022·宁夏·中考真题）北京冬奥会自由式滑雪空中技巧比赛中，某运动员比赛过程的空中剪影近似看作一条抛物线，跳台高度为米，以起跳点正下方跳台底端为原点，水平方向为横轴，竖直方向为纵轴，建立如图所示平面直角坐标系．已知抛物线最高点的坐标为，着陆坡顶端与落地点的距离为米，若斜坡的坡度（即．求：
(1)点的坐标；
(2)该抛物线的函数表达式；
(3)起跳点与着陆坡顶端之间的水平距离的长．（精确到米）（参考数据：）
45．（2022·山东烟台·统考中考真题）如图，某超市计划将门前的部分楼梯改造成无障碍通道．已知楼梯共有五级均匀分布的台阶，高AB＝0.75m，斜坡AC的坡比为1：2，将要铺设的通道前方有一井盖，井盖边缘离楼梯底部的最短距离ED＝2.55m．为防止通道遮盖井盖，所铺设通道的坡角不得小于多少度？（结果精确到1）
（参考数据表）
【考点10 解直角三角形应用之其他问题】
46．（2022·山东威海·模拟预测）激光电视的光源是激光，它运用反射成像原理，屏幕不通电无辐射，降低了对消费者眼睛的伤害．根据THX观影标准，当观影水平视场角“”的度数处于 到 之间时（如图1），双眼肌肉处于放松状态，是最佳的感官体验的观影位．
(1)小丽家决定要买一个激光电视，她家客厅的观影距离（人坐在沙发上眼睛到屏幕的距离）为3．5米，小佳家要选择电视屏幕宽（图2中的BC的长）在什么范围内的激光电视就能享受黄金观看体验？（结果精确到，参考数据： ， ，， ，，，，）
(2)由于技术革新和成本降低，激光电视的价格逐渐下降，某电器商行经营的某款激光电视今年每台销售价比去年降低4000元，在销售量相同的情况下，今年销售额在去年销售总额100万元的基础上减少，今年这款激光电视每台的售价是多少元？
47．（2022·浙江绍兴·一模）如图，图①是某电脑液晶显示器的侧面图，显示屏可以绕点O旋转一定的角度．研究表明：显示屏顶端A与底座B的连线与水平线BC垂直时(如图②)，人观看屏幕最舒适．此时测得，求的长度．(结果精确到)（参考数据：）
48．（2022·广东广州·校考二模）C919大型客机首飞成功，激发了同学们对航空科技的兴趣．如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸，图中，其中，求出线段BE和CD的长．
（，结果保留小数点后两位）
49．（2022·贵州六盘水·统考中考真题）“五一”节期间，许多露营爱好者在我市郊区露营，为遮阳和防雨会搭建一种“天幕”，其截面示意图是轴对称图形，对称轴是垂直于地面的支杆，用绳子拉直后系在树干上的点处，使得，，在一条直线上，通过调节点的高度可控制“天幕”的开合，m，m．
(1)天晴时打开“天幕”，若，求遮阳宽度（结果精确到0.1m）；
(2)下雨时收拢“天幕”，从65°减少到45°，求点下降的高度（结果精确到0.1m）．
（参考数据：，，，）
50．（2022·内蒙古通辽·统考中考真题）某型号飞机的机翼形状如图所示，根据图中数据计算的长度（结果保留小数点后一位，）.
计算器按键顺序
计算结果（已精确到0.001）
11.310
0.003
14.744
0.005