中考数学一轮复习专题20 矩形、菱形、正方形（10个高频考点）（强化训练）（2份，原卷版+解析版）

这是一份中考数学一轮复习专题20 矩形、菱形、正方形（10个高频考点）（强化训练）（2份，原卷版+解析版），文件包含中考数学一轮复习专题20矩形菱形正方形10个高频考点强化训练原卷版doc、中考数学一轮复习专题20矩形菱形正方形10个高频考点强化训练解析版doc等2份试卷配套教学资源，其中试卷共157页， 欢迎下载使用。
1．（2022·湖南湘西·统考中考真题）如图，在Rt△ABC中，∠A＝90°，M为BC的中点，H为AB上一点，过点C作CG∥AB，交HM的延长线于点G，若AC＝8，AB＝6，则四边形ACGH周长的最小值是（ ）
A．24B．22C．20D．18
【答案】B
【分析】通过证明△BMH≌△CMG可得BH＝CG，可得四边形ACGH的周长即为AB+AC+GH，进而可确定当MH⊥AB时，四边形ACGH的周长有最小值，通过证明四边形ACGH为矩形可得HG的长，进而可求解．
【详解】∵CG∥AB，
∴∠B＝∠MCG，
∵M是BC的中点，
∴BM＝CM，
在△BMH和△CMG中，
，
∴△BMH≌△CMG（ASA），
∴HM＝GM，BH＝CG，
∵AB＝6，AC＝8，
∴四边形ACGH的周长＝AC+CG+AH+GH＝AB+AC+GH＝14+GH，
∴当GH最小时，即MH⊥AB时四边形ACGH的周长有最小值，
∵∠A＝90°，MH⊥AB，
∴GH∥AC，
∴四边形ACGH为矩形，
∴GH＝8，
∴四边形ACGH的周长最小值为14+8＝22，
故选：B．
【点睛】本题主要考查全等三角形的判定与性质，确定GH的值是解题的关键．
2．（2022·四川乐山·统考中考真题）如图，等腰△ABC的面积为2，AB=AC，BC=2．作AE∥BC且AE=BC．点P是线段AB上一动点，连接PE，过点E作PE的垂线交BC的延长线于点F，M是线段EF的中点．那么，当点P从A点运动到B点时，点M的运动路径长为（ ）
A．B．3C．D．4
【答案】B
【分析】当P与A重合时，点F与C重合，此时点M在N处，当点P与B重合时，如图，点M的运动轨迹是线段MN．求出CF的长即可解决问题．
【详解】解：过点A作AD⊥BC于点D，连接CE，
∵AB=AC，
∴BD=DC=BC=1，
∵AE=BC，
∴AE=DC=1，
∵AE∥BC，
∴四边形AECD是矩形，
∴S△ABC=BC×AD=×2×AD=2，
∴AD=2，则CE=AD=2，
当P与A重合时，点F与C重合，此时点M在CE的中点N处，
当点P与B重合时，如图，点M的运动轨迹是线段MN．
∵BC=2，CE=2，
由勾股定理得BE=4，
cs∠EBC=，即，
∴BF=8，
∴CF=BF-BC=6,
∵点N是CE的中点，点M是EF的中点，
∴MN=CF=3，
∴点M的运动路径长为3，
故选：B．
【点睛】本题考查点的轨迹、矩形的判定和性质、解直角三角形、勾股定理等知识，解题的关键是正确寻找点M的运动轨迹，学会利用起始位置和终止位置寻找轨迹，属于中考填空题中的压轴题．
3．（2022·湖北宜昌·统考中考真题）如图，在矩形中，是边上一点，，分别是，的中点，连接，，，若，，，矩形的面积为________．
【答案】48
【分析】根据三角形中位线的性质，直角三角形斜边上中线等于斜边的一半得出相关线段长，利用勾股定理逆定理判定，再结合即可得出结论．
【详解】解：在矩形中，，
在矩形中，，分别是，的中点，，
是的中位线，即，
在中，是BE的中点，，
是斜边上的中线，即，
，
在中，是EC的中点，，
是斜边上的中线，即，
，
在中，，，，即，
是直角三角形，且，
过作于，如图所示：
，
故答案为：．
【点睛】本题考查矩形面积，涉及到中位线的性质、直角三角形斜边上的中线等于斜边的一半、矩形的性质、勾股定理逆定理、三角形等面积法等知识，熟练掌握相关性质，准确作出辅助线表示是解决问题的关键．
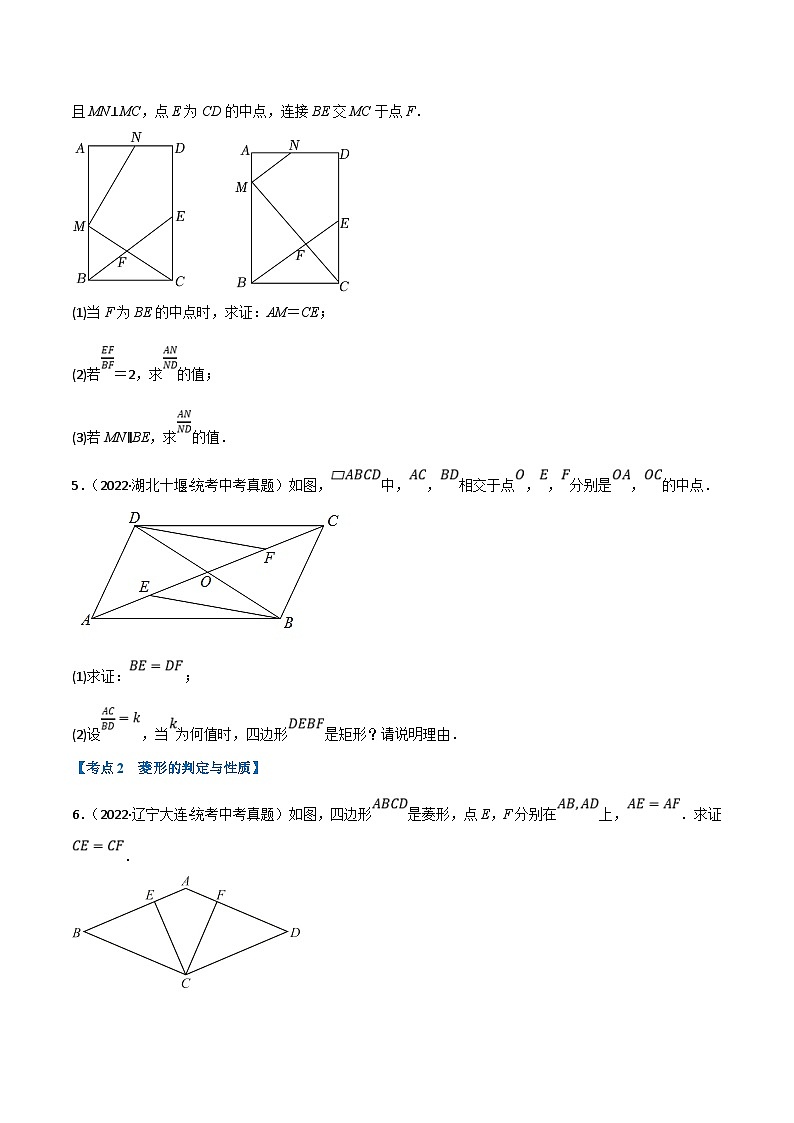
4．（2022·四川内江·统考中考真题）如图，在矩形ABCD中，AB＝6，BC＝4，点M、N分别在AB、AD上，且MN⊥MC，点E为CD的中点，连接BE交MC于点F．
(1)当F为BE的中点时，求证：AM＝CE；
(2)若＝2，求的值；
(3)若MN∥BE，求的值．
【答案】(1)见解析
(2)
(3)
【分析】(1)根据矩形的性质，证明△BMF≌ △ECF，得BM＝CE，再利用点E为CD的 中点，即可证明结论；
(2)利用△BMF∽△ECF，得，从而求出BM的长，再利用△ANM∽△BMC ，得 ，求出AN的长，可得答案；
(3)首先利用同角的余角相等得 ∠CBF＝ ∠CMB，则tan∠CBF＝tan∠CMB，得 ，可得BM的长，由（2）同理可得答案．
（1）
证明：∵F为BE的中点，
∴BF＝EF，
∵四边形ABCD是矩形，
∴AB∥CD，AB＝CD
∴∠BMF＝∠ECF，
∵∠BFM＝∠EFC，
∴△BMF≌△ECF（AAS），
∴BM＝CE，
∵点E为CD的中点，
∴CE＝CD，
∵AB＝CD，
∴，
∴，
∴AM＝CE；
（2）
∵∠BMF＝∠ECF，∠BFM＝∠EFC，
∴△BMF∽△ECF，
∴，
∵CE＝3，
∴BM＝，
∴AM＝，
∵CM⊥MN，
∴∠CMN＝90°，
∴∠AMN+∠BMC＝90°，
∵∠AMN+∠ANM＝90°，
∴∠ANM＝∠BMC，
∵∠A＝∠MBC，
∴△ANM∽△BMC，
∴，
∴，
∴，
∴DN＝AD﹣AN＝4﹣＝，
∴；
（3）
∵MN∥BE，
∴∠BFC＝∠CMN，
∴∠FBC+∠BCM＝90°，
∵∠BCM+∠BMC＝90°，
∴∠CBF＝∠CMB，
∴tan∠CBF＝tan∠CMB，
∴，
∴，
∴，
∴，
由（2）同理得，，
∴，
解得：AN＝，
∴DN＝AD﹣AN＝4﹣＝，
∴．
【点睛】本题是相似形综合题，主要考查了矩形的性质，全等三角形的判定与性质，相似三角形的判定与性质，三角函数等知识，求出BM的长是解决（2）和（3）的关键．
5．（2022·湖北十堰·统考中考真题）如图，中，，相交于点，，分别是，的中点．
(1)求证：；
(2)设，当为何值时，四边形是矩形？请说明理由．
【答案】(1)证明见解析
(2)当时，四边形是矩形，理由见解析
【分析】（1）连接，先根据平行四边形的性质可得，再根据线段中点的定义可得，然后根据平行四边形的判定可得四边形是平行四边形，最后根据平行四边形的性质即可得证；
（2）先根据矩形的判定可得当时，四边形是矩形，再根据线段中点的定义、平行四边形的性质可得，由此即可得出的值．
【详解】（1）证明：如图，连接，
四边形是平行四边形，
，
分别是，的中点，
，
四边形是平行四边形，
．
（2）解：由（1）已证：四边形是平行四边形，
要使平行四边形是矩形，则，
，
，即，
，
故当时，四边形是矩形．
【点睛】本题考查了平行四边形的判定与性质、矩形的判定等知识点，熟练掌握平行四边形的判定与性质是解题关键．
【考点2 菱形的判定与性质】
6．（2022·辽宁大连·统考中考真题）如图，四边形是菱形，点E，F分别在上，．求证．
【答案】证明见解析
【分析】由菱形的性质得到AB＝AD＝BC＝DC，∠B＝∠D，进而推出BE＝DF，根据全等三角形判定的“SAS”定理证得，由全等三角形的性质即可证出．
【详解】证明：∵四边形ABCD是菱形，
∴AB＝AD＝BC＝DC，∠B＝∠D，
∵AE＝AF，
∴AB﹣AE＝AD﹣AF，
∴BE＝DF，
在△BCE和△DCF中，，
∴，
∴CE＝CF．
【点睛】本题考查菱形的性质，全等三角形的判定与性质，解题的关键是综合运用相关知识解题．
7．（2022·浙江舟山·中考真题）小惠自编一题：“如图，在四边形中，对角线，交于点O，，，求证：四边形是菱形”，并将自己的证明过程与同学小洁交流．

若赞同小惠的证法，请在第一个方框内打“√”；若赞成小洁的说法，请你补充一个条件，并证明．
【答案】赞成小洁的说法，补充，见解析
【分析】赞成小洁的说法，补充：，由四边相等的四边形是菱形即可判断．
【详解】赞成小洁的说法，补充：．
证明： ，，
，．
又∵．
∴，
∴四边形是菱形．
【点睛】本题考查菱形的判定以及线段垂直平分线的性质，熟练掌握菱形的判定是解题的关键．
8．（2022·山西吕梁·统考三模）综合与实践：
数学活动课上，老师让同学们根据下面情境提出问题并解答．
问题情境：在中，点P是边上一点．将沿直线折叠，点D的对应点为E．
“兴趣小组”提出的问题是：如图1，若点P与点A重合，过点E作，与交于点F，连接，则四边形是菱形．
(1)数学思考：请你证明“兴趣小组”提出的问题；
(2)拓展探究：“智慧小组”提出的问题是：如图2，当点P为的中点时，延长交于点F，连接．试判断与的位置关系，并说明理由．
请你帮助他们解决此问题．
(3)问题解决：“创新小组”在前两个小组的启发下，提出的问题是：如图3，当点E恰好落在边上时，，，．则的长为___________．（直接写出结果）
【答案】(1)见解析
(2)，理由见解析
(3)
【分析】（1）先证明，得到两组对边分别平行，再用邻边相等的平行四边形是菱形判定，也可以用四条边相等的四边形是菱形进行判断；
（2）证明△PAF≌△PEF，得到∠APF=∠FPE，再由折叠得到∠DPC=∠EPC，从而证明∠FPC=90°；
（3）延长BA、CP相交于点F，得△AFP∽△DCP，再证EF=CE即可求出结果．
（1）
证法一：由折叠得，，，
∵
∴
∴
∴
∴四边形是平行四边形
∵
∴四边形是菱形．
证法二：
证明：由折叠得，，，
∵
∴
∴
∴
∴
∴四边形是菱形．
（2）
解： ．
连接
由折叠可得，，
∵四边形是平行四边形
∴
又∵
∴
∵点P是的中点
∴
∴
∴
∴
∴
∴（SSS）
∴
又∵，即
∴
∴．
（3）
解：延长BA、CP相交于点F，
由题意，△AFP∽△DCP
∴ 即
∴
∵∠DCP=∠ECP，∠DCP=∠F
∴∠F=∠ECP
∴EF=EC=DC=10
∴．
故答案为．
【点睛】本题考查折叠、平行四边形、相似、菱形的判定等，属于综合性题目，解题关键在于灵活运用几何知识，构造常见的模型．
9．（2022·黑龙江哈尔滨·统考一模）如图矩形中，对角线的垂直平分线与相交于点M，与相交于点O，与相交于N，连接、；
(1)求证：四边形是菱形；
(2)若，，求的面积．
【答案】(1)证明见解析
(2)50
【分析】（1）由矩形的性质可得，，，证明，则，四边形是平行四边形，由垂直平分线的性质可知，进而结论得证；
（2）由，设，，在中，勾股定理求得，则，，在中，由勾股定理得，，在中，由勾股定理得，计算求出满足要求的值，进而可得，的值，根据计算求解即可．
（1）
证明：由矩形的性质可得，，，
∴，，
在和中
∵，
∴，
∴，
∴四边形是平行四边形，
∵垂直平分，
∴，
∴是菱形．
（2）
解：∵，设，，
在中，由勾股定理得，
∴，，
在中，由勾股定理得，
∴，
∵，
在中，由勾股定理得，即，
解得，（不合题意，舍去）,
∴，，
∴，
∴的面积为50．
【点睛】本题考查了矩形的性质、全等三角形的判定与性质、垂直平分线的性质、菱形的判定、正切、勾股定理等知识．解题的关键在于对知识的熟练掌握与灵活运用．
10．（2022·浙江宁波·统考二模）如图1，平行四边形中，，，点是边上的点，连结，以为对称轴作的轴对称图形．
(1)如图2，当点正好落在边上时，判断四边形的形状并说明理由；
(2)如图1，当点是线段的中点且时，求的长；
(3)如图3，当点三点共线时，恰有，求的长．
【答案】(1)菱形，理由见解析
(2)9
(3)
【分析】（1）画出图形，根据对称及平行四边形的性质证明即可；
（2）连结，交于H，先证明，再分别利用勾股定理求出AH和PH的值即可；
（3）证明即可求出DQ的长度，最后根据计算即可．
（1）
四边形的是菱形，理由如下：
与关于对称，
，，．
点Q正好落在边上，
．
，
．
，
∴．
四边形是菱形．
（2）
连结，交于H，
，，
是中垂线．
又是线段的中点，
．
．
∴．
，，
∴，
．
（3）
，
．
又，
．
，
．
．
又，
．
，即，
解得．
．
【点睛】本题考查了平行四边形的性质、翻折变换、菱形的性质与判定、相似三角形的性质与判定等知识，解题的关键是根据不同题意画出对应的图形，属于中考常考题型．
【考点3 正方形的判定与性质】
11．（2022·海南海口·海南华侨中学校联考模拟预测）如图①，在正方形中，点E、F、G、H分别在边、、、上，若，
(1)求证：；
(2)如果把题目中的“正方形”改为“长方形”、若，（如图②），求的值；
(3)如果把题目中的“”改为“与的夹角为45°”（如图③），若正方形的边长为2，的长为，求的长．
【答案】(1)见详解
(2)
(3)
【分析】（1）过点作交于，过点作交于，证明即可求解；
（2）过点作交于，过点作交于，由（1）可得，再由，可求；
（3）过作交于，过作交于，以为旋转中心，绕点顺时针旋转到，可证明，设，则，，在中，，求出，在中，求出，再由即可求解．
【详解】（1）证明：过点作交于，过点作交于，
四边形是正方形，
，
，
，
，
；
（2）解：过点作交于，过点作交于，
由（1）可得，，
∴，
，
，，
，，
；
（3）解：过作交于，过作交于，以为旋转中心，绕点顺时针旋转到，
，，
，
与的夹角为，
，
，
，
，
，
，
设，则，，
在中，，
解得，
，
在中，，
．
【点睛】本题考查了四边形的综合应用，熟练掌握正方形的性质，矩形的性质，直角三角形的性质，三角形全等的判定及性质，相似三角形的判定及性质，数形结合解题是关键．
12．（2022·山东济南·统考模拟预测）（1）【问题情境】如图，四边形是正方形，点是边上的一个动点，以为边在的右侧作正方形，连接、，则与的数量关系是______；
（2）【类比探究】如图，四边形是矩形，，，点是边上的一个动点，以为边在的右侧作矩形，且，连接、．判断线段与有怎样的数量关系和位置关系，并说明理由；
（3）【拓展提升】如图3，在（2）的条件下，连接，则的最小值为______．
【答案】（1）；（2）．理由见解析；（3）
【分析】（1）通过证明全等，得到；
（2）通过证明得到，，延长相交于点H．可以证明；
（3）作于N，交的延长线于M．首先证明点G的运动轨迹是线段，将的最小值转化为求的最小值．
【详解】解：，
理由：
∵正方形，
∴，
∵正方形，
∴，
∴，
∴，
在和中，
，
∴，
∴；
（2）解：．
理由如下：延长相交于点H．
∵矩形、矩形，
∴，
∴，
∵，，
∴，
∵，
∴，
∴，，
∴，
∵矩形，
∴，
∴，，
∴，
∴；
（3）解：作于N，交的延长线于M．
∵，
∴，
∴，
∴，
∴，
∵，
∴，
∴点G的运动轨迹是直线，
作点D关于直线的对称点，连接交于G，此时的值最小，最小值为，
由（2）知，，
∴，
∴，
∴的最小值就是的最小值．
∵，
∴的最小值为，
故答案为：．
【点睛】本题考查了正方形的性质、矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质．在判断全等和相似时出现“手拉手”模型证角相等．这里注意利用三边关系来转化线段的数量关系求出最小值．
13．（2022·贵州贵阳·统考二模）如图，已知四边形ABCD是正方形，AB＝，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE，EF为邻边作矩形DEFG，连CG．
(1)求证：矩形DEFG为正方形；
(2)求证：CE＋CG＝8
【答案】(1)见解析
(2)见解析
【分析】（1）过点作EM⊥BC于M，EN⊥CD于N，证，得，即可证矩形为正方形；
（2）证明，可得，由此可推得，利用勾股定理计算即可．
(1)
证明：如图，过点作EM⊥BC于M，EN⊥CD于N，则∠MEN＝90°．
四边形是正方形，
平分，
又 ，，
．
，
，，
．
在△DEN和△FEM中，
，
．
，
矩形是正方形．
(2)
证明：四边形与四边形为正方形，
∴DE＝DG，，，
∠ADE+∠CDE＝∠CDG+∠CDE＝90°，
∴∠ADE＝∠CDG，
在与中，
，
∴△ADE≌△CDG（SAS），
∴AE＝CG．
∴．
【点睛】本题考查了正方形的性质与判定，角平分线的性质定理，全等三角形的性质与判定，勾股定理，解决本题的关键是熟练运用相关性质定理．
14．（2022·贵州黔西·统考中考真题）如图1，在正方形ABCD中，E，F分别是BC，CD边上的点（点E不与点B，C重合），且．
(1)当时，求证：；
(2)猜想BE，EF，DF三条线段之间存在的数量关系，并证明你的结论；
(3)如图2，连接AC，G是CB延长线上一点，，垂足为K，交AC于点H且．若，，请用含a，b的代数式表示EF的长．
【答案】(1)见解析
(2)，见解析
(3)
【分析】（1）先利用正方表的性质求得，，再利用判定三角形全等的“SAS”求得三角形全等，然后由全等三角形的性质求解；
（2）延长CB至M，使，连接AM，先易得，推出，，进而得到，最后利用全等三角形的性质求解；
（3）过点H作于点N，易得，进而求出，再根据（2）的结论求解．
（1）
证明：∵四边形ABCD是正方形，
∴，．
在和中
，
∴，
∴；
（2）
解：BE，EF，DF存在的数量关系为．
理由如下：
延长CB至M，使，连接AM，
则．
在和中
，
∴，
∴，．
∵，
∴．
∴∠MAE=∠FAE，
在和中
，
∴，
∴EM=EF，
∵EM=BE+BM，
∴；
（3）
解：过点H作于点N，
则．
∵，
∴，
∴．
在和中
，
∴，
∴．
∵，，
∴，
∴，
由（2）知，．
【点睛】本题主要考查了正方形的性质，全等三角形的判定和性质，特殊角的三角函数值，作出辅助线，构建三角形全等是解答关键．
15．（2022·四川德阳·模拟预测）已知：四边形是正方形，点在边上，点在边上，且．

(1)如图，与有怎样的关系．写出你的结果，并加以证明；
(2)如图，对角线与交于点．，分别与，交于点，点．
①求证：；
②连接，若，，求的长．
【答案】(1)；．证明见解析
(2)①见解析；②
【分析】（1）根据正方形的性质可得，，然后利用“边角边”证明，根据全等三角形对应角相等可得，，然后求出，再求出，然后根据垂直的定义解答即可；
（2）①根据正方形的对角线互相垂直平分可得，，对角线平分一组对角可得，然后求出，再利用“角边角”证明，根据全等三角形对应边相等可得；②过点作于，作于，根据全等三角形对应角相等可得，再利用“角角边”证明，根据全等三角形对应边相等可得，然后判断出四边形是正方形，根据正方形的性质求出，再求出，然后利用勾股定理列式求出，再根据正方形的性质求出即可．
【详解】（1）解：；．
证明：四边形是正方形，
，，
在和中，
，
，
，，
，
，
，
；
（2）①证明：四边形是正方形，
，，，
，
，
即，
在和中，
，
，
；
②解：如图，过点作于，作于，
，
，
在和中，
，
，
，
四边形是正方形，
，
，
，
，
在中，，
正方形的边长．
【点睛】本题是四边形综合题型，主要利用了正方形的性质，全等三角形的判定与性质，（2）②难度较大，作辅助线构造出全等三角形和以为对角线的正方形是解题的关键，也是本题的难点
【考点4 特殊四边形中的折叠变换】
16．（2022·吉林长春·统考二模）【感知】如图①，中，，，易知（不需要证明）．
【探究】如图②，四边形是一张边长为2的正方形纸片，、分别为、的中点，沿过点的折痕将纸片翻折，使点落在上的点A'处，折痕交于点，求的度数和的长．
【拓展】若矩形纸片按如图③所示的方式折叠，、两点恰好重合于一点（如图④），若，直接写出的长．
【答案】【探究】15°；【拓展】4
【探究】由折叠的性质可知，，，由，可得，可知，进而得出，，利用折叠性质就可求的度数；在中，根据勾股定理可求出，，通过角的计算，可得出，可得出；
【拓展】利用折叠的性质可知四边形是菱形，折叠后构成的六个小的直角三角形全等，可得出，是等边三角形，，由，可得．
【详解】探究：解：∵正方形边长为2，、为、的中点，
∴边长，
沿过点的折痕将纸片翻折，使点落在上的点处，
∴，
∴，
∴，
可得，
沿折叠落在处，
∴，，
∴，
，，
∴，
∴，
，
∴，
∴，
则；
拓展：解：∵四边形是矩形，
∴ ，
∴∠DFA=∠FAE，∠FCE=∠CEB，
由折叠得∠DFA=∠AFO，∠OEC=∠CEB，
∴∠EAF=∠AFO，∠FEC=∠FCE，
∴EA=EF，EF=FC，
∴EA=FC，
∴DF=EB，
由折叠得DF=OF，BE=OE，
∴OF=OE，
由折叠的性质可知：
，，
∵，，，
∴，
∴
∴A、O、C三点共线，E、O、F三点共线，且AC与EF互相平分，
又∵∠AOF=90°，
∴，
∴四边形是菱形，
结合折叠的性质和菱形的性质，可知：
，，
∴，
∴∠FAE=∠BEC=60°，
∵，
∴是等边三角形，
在中，，
∴
∴，
∵，
∴，
∴．
【点睛】本题考查了含30°的直角三角形的性质、折叠的性质、菱形的判定及性质、等边三角形的判定及性质等知识，把握正方形、矩形折叠的性质是解决本题的关键．
17．（2022·吉林长春·模拟预测）【推理】
如图1，在边长为10的正方形中，点是上一动点，将正方形沿着折叠，点落在点处，连结，，延长交于点，与交于点．
(1)求证：．
【运用】
(2)如图2，在【推理】条件下，延长交于点．若，求线段DH的长．
【拓展】
(3)如图3，在【推理】条件下，连结．则线段的最小值为 ．
【答案】(1)见解析
(2)
(3)
【分析】（1）利用证明，得；
（2）连接，利用等角对等边证明，设，则，由勾股定理得，，解方程即可；
（3）取的中点，连接，，利用勾股定理求出，直角三角形斜边上中线的性质得的长，再利用三角形三边关系可得答案．
【详解】（1）证明：∵四边形是正方形，
∴，，
∴，
∵正方形沿折叠，
∴，
∴，
∴，
∴，
∴；
（2）解：连接，
∵正方形沿折叠，
∴，，
∵，
∴，
∵，
∴，
∴，
设，则，
由勾股定理得，，
解得，
∴；
（3）解：取的中点，连接，，
则，，
∵，为的中点，
∴，
∵，
∴的最小值为，
故答案为：．
【点睛】本题是四边形综合题，主要考查了正方形的性质，翻折的性质，全等三角形的判定与性质，勾股定理，三角形三边关系等知识，运用勾股定理列方程是解题的关键．
18．（2022·河南信阳·统考模拟预测）学习了菱形的判定后，小张同学与小刘同学讨论探索折纸中的菱形．
小张：如图①，两张相同宽度的矩形纸条重叠部分（阴影部分）是一个菱形．
小刘：如图②，一张矩形纸条沿折叠后，重叠部分展开（阴影部分）后是一个菱形．
(1)小张同学的判断是否正确？
(2)小刘同学的判断是否正确？如果正确，以小刘的方法为例，证明他的判断；如果不正确，请说明理由．
(3)如图③，矩形的宽，若，沿折叠后，重叠部分展开（阴影部分）后得到菱形，求菱形的面积．
【答案】(1)正确
(2)正确，理由见解析
(3)20
【分析】（1）由两个纸条是矩形可得，，得到四边形是平行四边形，根据两张矩形纸条宽度相同，利用两个三角形全等得到邻边相等即可证明；
（2）根据折叠确定邻边相等，再根据矩形性质及折叠可确定四边形是平行四边形，从而根据邻边相等的四边形是菱形即可得证；
（3）根据平行四边形的面积公式，已知高，设，则，
在中，由勾股定理得到，进而得，代入公式求解即可．
（1）
解：正确．
理由如下：由两个纸条是矩形可得，，
四边形是平行四边形，
，
过作，垂足为，如图所示：
两张矩形纸条宽度相同，
，
在和中，
，
，
，
四边形是菱形；
（2）
解：正确．
理由如下：由是矩形可得，
由轴对称的性质可知，，
∵，
∴，
∴，
∴，，
又∵，
∴四边形为平行四边形，
∵，
∴四边形为菱形，
（3）
解：∵，
∴，
∵四边形为菱形，
∴，
设，则，
在中，由勾股定理，得，解得，
∴，
∴菱形的面积．
【点睛】本题考查的是图形的翻折变换、矩形的性质、菱形的判定与性质、勾股定理求线段长、菱形面积公式，熟知图形翻折变换的性质是解答此题的关键．
19．（2022·云南昆明·云大附中校考三模）综合与实践
在数学教学中，教师和学生都学习到了新知识，掌握了许多新技能．例如教材八年级下册的数学活动——折纸，就引起了许多同学的兴趣．在经历图形变换的过程中，进一步发展了同学们的空间观念，积累了数学活动经验．
实践发现：
对折矩形纸片ABCD，使AD与BC重合，折痕为EF，把纸片展平：再一次折叠纸片，使点A落在EF上的点N处，并使折痕经过点B，折痕为BM，把纸片展平，连接AN，如图①；
(1)折痕BM所在直线是否是线段AN的垂直平分线？请判断图中是什么特殊三角形？请写出解答过程．
(2)继续折叠纸片，使点A落在BC边上的点H处，并使折痕经过点B，得到折痕BG，把纸片展平，如图②，求∠GBN的度数．
(3)拓展延伸：
如图③，折叠矩形纸片ABCD，使点A落在BC边上的点处，并且折痕交BC边于点T，交AD边于点S，把纸片展平，连接交ST于点O，连接AT；求证：四边形是菱形．
【答案】(1)折痕BM所在直线是线段AN的垂直平分线，是等边三角形，过程见解析
(2)
(3)见解析
【分析】（1）由折叠的性质可得AN＝BN，AE＝BE，∠NEA＝90°，BM垂直平分AN，∠BAM＝∠BNM＝90°，可证△ABN是等边三角形；
（2）由折叠的性质可得∠ABG＝∠HBG＝45°，可求解；
（3）由折叠的性质可得AO＝A'O，AA'⊥ST，由“AAS”可证△ASO≌△A'TO，可得SO＝TO，由菱形的判定可证四边形SATA'是菱形．
（1）
解：如图①，
∵对折矩形纸片ABCD，使AD与BC重合，
∴EF垂直平分AB，
∴AN＝BN，AE＝BE，∠NEA＝90°，
∵再一次折叠纸片，使点A落在EF上的点N处，
∴BM垂直平分AN，∠BAM＝∠BNM＝90°，
∴AB＝BN，
∴AB＝AN＝BN，
∴△ABN是等边三角形，
（2）
解：∵折叠纸片，使点A落在BC边上的点H处，
∴∠ABG＝∠HBG＝45°，
∴∠GBN＝∠ABN﹣∠ABG＝15°，
（3）
证明：∵折叠矩形纸片ABCD，使点A落在BC边上的点A'处，
∴ST垂直平分AA'，
∴AO＝A'O，AA'⊥ST，
∵AD∥BC，
∴∠SAO＝∠TA'O，∠ASO＝∠A'TO，
∴（AAS）
∴SO＝TO，
∴四边形ASA'T是平行四边形，
又∵AA'⊥ST，
∴四边形SATA'是菱形．
【点睛】本题是四边形综合题，考查了矩形的性质，菱形的判定，全等三角形的判定和性质，折叠的性质，等边三角形的判定和性质等知识，灵活运用这些性质进行推理是本题的关键．
20．（2022·湖北武汉·校考三模）（1）如图，在正方形中，是上一动点，将正方形沿着折叠，点落在点处，连接，并延长交于点求证：；
（2）在（1）的条件下，如图，延长交边于点若，求的值；
（3）如图，四边形为矩形，同样沿着折叠，连接，延长分别交于两点，若，则的值为___________（直接写出结果）
【答案】（1）见解析；（2）；（3）
【分析】根据证明三角形全等即可；
如图中，连接根据，求出即可解决问题；
如图中，连接由，可以设，根据相似三角形的判定和性质可得，则，利用勾股定理构建方程求解即可．
【详解】证明：如图中，
是由折叠得到，
，
，
四边形是正方形，
，
，
，
在和中，
，
；
解：如图中，连接．
，
，
由折叠可知，
，
四边形是正方形，
，
，
，
，
，
，
设，则，
，
设，
，
由折叠可知，
，
，
，
或舍弃，
，
；
解：如图中，连接．
由，
设，
由知，
，
由折叠可知，
，
，
，
，
，
，
，
，
，
，

，
，
或舍弃，
，
．
【点睛】本题属于四边形综合题，考查了正方形的性质，折叠的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找全等三角形或相似三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．
【考点5 特殊四边形中的平移变换】
21．（2022·安徽合肥·合肥市第四十五中学校考三模）我们把连接菱形对边中点得到的所有菱形称作如图①所示基本图的特征图形显然这样的基本图共有5个特征图形．将此基本图不断复制并平移，使得相邻两个基本图的一个顶点与对称中心重合，这样得到图1、图2、图3…
(1)观察以上图形并完成下表：
猜想：在图中，特征图形的个数为______；（用含的式子表示）
(2)已知基本图的边长为4，一个内角恰好为，求图20中所有特征图形的面积之和．
【答案】(1)，
(2)图20中所有特征图形的面积之和为
【分析】（1）根据从第2个图形开始，每多一个基本图形就会多出4个菱形解答即可；
（2）根据图形的特征解决问题即可．
(1)
解：观察图形和表可得：
图1中的特征图形的个数为：，
图2中的特征图形的个数为：，
图3中的特征图形的个数为：，
∴图4中的特征图形的个数为：，
∴图中的特征图形的个数为：．
故答案为：，
(2)
如图，过点作于，
根据题意知基本图的边长为4，一个内角恰好为，
即菱形的边长为4，一个内角恰好为，
∴，，
∴在中，，
∴，
∴大的特征图形面积为，小的特征图形面积为，
由（1）知，图20中共有特征图形：（个），
其中有20个大的特征图形，61个小的特征图形，
∴图20中所有特征图形的面积之和为：．
∴图20中所有特征图形的面积之和为．
【点睛】本题考查平移设计图案，规律型问题，涉及到菱形的面积计算和三角函数等知识．解题的关键是学会探究规律的方法．
22．（2022·福建厦门·厦门双十中学校考二模）如图，四边形ABCD是矩形，平移线段AB至EF，其中点A的对应点为点E，点B的对应点为点F，且点E恰好落在边BC上．
(1)若AF＝DF，求证：点E为BC中点；
(2)若BC＝k AB，＜k＜2，是否存在∠BFC＝90°？请说明理由．
【答案】(1)见解析
(2)若BC＝k AB，＜k＜2，不存在∠BFC＝90°，理由见解析
【分析】（1）根据AF=DF，可得∠DAF=∠ADF，从而得到∠BAF=∠CDF，可证得△BAF≌△CDF，从而得到BF=CF，即可求证；
（2）假设∠BFC=90°，则∠FBC+∠FCB=90°，可证得△BEF∽△FEC，从而得到，然后设BE=x，可得，从而得到，进而得到该方程没有实数根，即可求解．
（1）
证明∶ ∵四边形ABCD是矩形，
∴AB=CD，∠BAD=∠ADC=∠ABC=90°，
∵AF=DF，
∴∠DAF=∠ADF，
∴∠BAF=∠CDF，
在△BAF和△CDF中，
∵AB=CD，∠BAF=∠CDF，AF=DF，
∴△BAF≌△CDF（SAS），
∴BF=CF，
由平移可知：EF∥AB，
∴∠BEF=∠ABC=90°，即EF⊥BC，
∴点E为BC的中点；
（2）
若BC＝k AB，＜k＜2，不存在∠BFC＝90°，理由如下：
假设∠BFC=90°，则∠FBC+∠FCB=90°，
由平移可知：EF∥AB，EF=AB，
∴∠BEF=∠ABC=90°，即EF⊥BC，
∴∠BEF=∠CEF=90°，
∴∠FBC+∠BFE=90°，
∴∠FCB=∠BFE，
∴△BEF∽△FEC，
∴，即，
∴，
设BE=x，
∵BC＝k AB，
∴，
∴，
整理得：，
∴，
∵＜k＜2，
∴，
∴，
∴，
∴该方程没有实数根，
即不存在BE，使，
∴若BC＝k AB，＜k＜2，不存在∠BFC＝90°．
【点睛】本题主要考查了矩形的性质，等腰三角形的性质，全等三角形和相似三角形的判定和性质，一元二次方程根的判别式，熟练掌握矩形的性质，等腰三角形的性质，全等三角形和相似三角形的判定和性质，一元二次方程根的判别式是解题的关键．
23．（2022·云南德宏·统考模拟预测）如图，将△ABC沿射线AB平移4cm后能与△BDE完全重合，连接CE、CD交BE于点O，OB＝OC．
(1)求证：四边形CBDE为矩形；
(2)若S△BOC＝cm2，求∠ACD的度数．
【答案】(1)见解析
(2)120°
【分析】（1）由平移的性质及判定定理可证得，根据全等三角形的性质即可求证结论．
（2）根据矩形的性质及面积公式即可求得，进而可利用特殊三角函数值可求得，根据垂直平分线的性质即可求解．
【详解】（1）证明：由题意可知：△BDE由△ABC平移后得到，
∴，且，
∴四边形是平行四边形，
∴，且，
∴，，
在和中
，
∴
∴，，
又∵，
∴，
∴ 平行四边形为矩形．
（2）由（1）可知四边形为矩形，
∴，且cm，
在中过点作的垂线，垂足为，则，
∵，
∴cm，
∴在，，
∴，
又∴在△ACD中，BC是AD的垂直平分线，
∴，
∴，
∠ACD的度数为．
【点睛】本题考查了平移的性质、全等三角形的判定及性质、矩形的判定及性质、特殊三角函数值求角度，熟练掌握相关性质及判定定理是解题的关键．
24．（2022·山东淄博·统考二模）已知，矩形ABCD，点E在AB上，点G在AD，点F在射线BC上，点H在CD上．
(1)如图1，当矩形ABCD为正方形时，且DE⊥GF，求证：BF=AE+AG；
(2)在（1）的条件下，将GF沿AD向右平移至点G与点D重合，如图2，连接EF，取EF的中点P，连接PC，试判断BE与PC的数量关系，并说明理由；
(3)如图3，点F在BC上，连接EH，EH交FG于O，∠GOH=45°，若AB=2，BC=4，FG=，求线段EH的长．
【答案】(1)见解析
(2)BE=CP，理由见解析
(3)线段EH的长为．
【分析】（1）作GM⊥BC于M．证△DAE≌△GMF，得AE=FM，AG=BM．所以BF=AE+AG；
（2）作EQ∥CP交BC于Q．证EQ=2CP，EQ=BE可得BE=CP；
（3）作BM∥GF交AD于M，作BN∥EH交CD于N，取AD 的中点I，取BC的中点J，得四边形ABJI是正方形，延长IJ到L，使JL=AM=1，证明△BAM≌△BJL（SAS），再证明△MBK≌△LBK（SAS），推出MK=KL，设KJ=x，则MK=KL=KJ+JL=x+1，IK=2-x，在Rt△IMK中，由勾股定理求得x 的值，再利用平行线分线段成比例定理可得．
（1）
解：如图1，过点G作GM⊥BC于M，
则∠GMB=∠GMF=90°，
∵四边形ABCD是正方形，
∴AD=AB，∠A=∠B=90°，
∴四边形ABMG是矩形，
∴AG=BM，
∵DE⊥GF，
∴∠ADE+∠DGF=∠ADE+∠AED=90°，
∴∠AED=∠DGF，
又∠DGF=∠MFG，
∴∠AED=∠MFG，
∴△DAE≌△GMF（AAS），
∴AE=MF，
则BF=BM+MF=AG+AE；
（2）
解：BE=CP，理由如下：
如图2，过点E作EQ∥PC，交BC于点Q，
∵P是EF的中点，
∴PC是△EQF的中位线，
则EQ=2PC，QC=CF，
∵∠ADC=∠EDF=90°，
∴∠ADE=∠CDF，
又∵∠A=∠DCF=90°，AD=CD，
∴△ADE≌△CDF（ASA），
∴AE=CF=QC，
∵AB=BC，
∴BE=BQ，
则∠BEQ=45°，
∴EQ=BE，
则2PC=BE，
∴BE=PC；
（3）
解：如图所示，作BM∥GF交AD于M，作BN∥EH交CD于N，
则四边形BFGM和四边形BEHN是平行四边形，
∴BM=GF=，BN=EH，
∵AB=2，∴AM=1，
取AD 的中点I，取BC的中点J，连接IJ，
∵AB=2，BC=4，
∴AI=BJ=2，
∴四边形ABJI是正方形，
∴MI=1，AB=BJ=2，
延长IJ到L，使JL=AM=1，IJ交BN于点K，
∵BA=BC，∠A=∠BJI=∠BJL=90°，
∴△BAM≌△BJL（SAS），
∴∠ABM=∠JBL，BM=BL=，
∵∠GOH=45°，BN∥EH，BM∥GF，
∴∠MBN=∠MBK=45°，
∴∠ABM+∠JBK=45°，
∴∠JBL+∠JBK=45°，即∠LBK=45°，
∴△MBK≌△LBK（SAS），
∴MK=KL，
设KJ=x，则MK=KL=KJ+JL=x+1，IK=2-x，
在Rt△IMK中，由IM2+IK2=MK2可得12+（2-x）2=（x+1）2，
解得x=，即KJ=，
则BK==，
∵四边形ABCD是矩形，四边形ABJI是正方形，点J是BC的中点，
∴KJ∥CN，
∴，
∴BN=2BK=．
∴线段EH的长为．
【点睛】本题是四边形的综合题，解题的关键是掌握正方形的判定和性质，全等三角形的判定和性质，勾股定理，平行四边形的判定与性质，三角形中位线定理等知识点．
25．（2022·辽宁沈阳·统考一模）已知正方形ABCD，在边DC所在的直线上有一动点E，连接AE，一条与射线AE垂直的直线l沿射线AE方向，从点A开始向上平移，垂足为点P，交边AD所在直线于点F．
(1)如图1所示，当直线l经过正方形ABCD的顶点B时．求证：；
(2)如图2所示，当直线l经过AE的中点时，与对角线BD交于点G，连接EG，CG．求证：；
(3)直线l继续向上平移，当点P恰好落在对角线BD所在的直线上时，交边CB所在的直线于点H，当，，请直接写出的长．
【答案】(1)见解析
(2)见解析
(3)或6
【分析】（1）证明△ABF≌△DAE（ASA），可得结论．
（2）连接AQ，CQ．想办法证明△AQF是等腰直角三角形即可解决问题．
（3）分成若点E在线段CD上时与点E在CD的延长线上时两种情况进行讨论，可得结论．
【详解】（1）证明：∵四边形ABCD是正方形，
∴AB=AD，∠D=∠BAD=90°，
∵AE⊥BF，
∴∠APB=90°，
∴∠PAD+∠PAB=90°，∠PAB+∠ABF=90°，
∴∠ABF=∠DAE，
∴△ABF≌△DAE（ASA），
∴AF=DE．
（2）证明：连接AG，如图所示，
∵AE⊥FG，AP=EP，
∴GE=GA，
∵四边形ABCD是正方形，
∴BA=BC，∠ABG=∠CBG，
∵BG=BG，
∴△ABG≌△CBG（SAS），
∴GA=GC，
∴GE=GC；
（3）如图，若点E在线段CD上时，过点F作FT⊥BC，垂足为点T，
则四边形DFTC是矩形．
∴FT=DC，∠ADE=∠FTH=90°，
∵四边形ABCD是正方形，
∴AB=CD=BC，
∵AE⊥FH，
∴∠APF=90°，
∵∠DAE+∠AFP=90°，∠AFP+∠TFH=90°，
∴∠DAE=∠TFH，
∵∠ADE=∠FTH，AB=FT，
∴△ADE≌△FTH（ASA），
∴DE=TH，
∵AB∥CD，AD∥BC，
∴，
∴，
∵BC=3，
∴
∴BH=，
同理，若点E在CD的延长线上时，可得BH=6，
故答案为：或6
【点睛】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，平行线分线段成比例定理，等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
【考点6 特殊四边形中的旋转变换】
26．（2022·江苏南通·统考中考真题）如图，矩形中，，点E在折线上运动，将绕点A顺时针旋转得到，旋转角等于，连接．
(1)当点E在上时，作，垂足为M，求证；
(2)当时，求的长；
(3)连接，点E从点B运动到点D的过程中，试探究的最小值．
【答案】(1)见详解
(2)或
(3)
【分析】（1）证明即可得证．
（2）分情况讨论，当点E在BC上时，借助，在中求解；当点E在CD上时，过点E作EG⊥AB于点G，FH⊥AC于点H，借助并利用勾股定理求解即可．
（3）分别讨论当点E在BC和CD上时，点F所在位置不同，DF的最小值也不同，综合比较取最小即可．
（1）
如图所示，
由题意可知，，，
，
由旋转性质知：AE=AF，
在和中，
，
，
．
（2）
当点E在BC上时，
在中，，，
则，
在中，，，
则，
由（1）可得，，
在中，，，
则，
当点E在CD上时，如图，
过点E作EG⊥AB于点G，FH⊥AC于点H，
同（1）可得，
，
由勾股定理得；
故CF的长为或．
（3）
如图1所示，当点E在BC边上时，过点D作于点H，
由（1）知，，
故点F在射线MF上运动，且点F与点H重合时，DH的值最小．
在与中，
，
，
，
即，
，，
，
在与中，
，
，
，
即，
，
故的最小值；
如图2所示，当点E在线段CD上时，将线段AD绕点A顺时针旋转的度数，得到线段AR，连接FR，过点D作，，
由题意可知，，
在与中，
，
，
，
故点F在RF上运动，当点F与点K重合时，DF的值最小；
由于，，，
故四边形DQRK是矩形；
，
，
，
，
故此时DF的最小值为；
由于，故DF的最小值为．
【点睛】本题考查矩形的性质、全等三角形的判定和性质、相似三角形的性质和判定、勾股定理、解直角三角形，解决本题的关键是各性质定理的综合应用．
27.（2022·江西·统考中考真题）问题提出：某兴趣小组在一次综合与实践活动中提出这样一个问题：将足够大的直角三角板的一个顶点放在正方形中心O处，并绕点O逆时针旋转，探究直角三角板与正方形重叠部分的面积变化情况（已知正方形边长为2）．
(1)操作发现：如图1，若将三角板的顶点P放在点O处，在旋转过程中，当与重合时，重叠部分的面积为__________；当与垂直时，重叠部分的面积为__________；一般地，若正方形面积为S，在旋转过程中，重叠部分的面积与S的关系为__________；
(2)类比探究：若将三角板的顶点F放在点O处，在旋转过程中，分别与正方形的边相交于点M，N．
①如图2，当时，试判断重叠部分的形状，并说明理由；
②如图3，当时，求重叠部分四边形的面积（结果保留根号）；
(3)拓展应用：若将任意一个锐角的顶点放在正方形中心O处，该锐角记为（设），将绕点O逆时针旋转，在旋转过程中，的两边与正方形的边所围成的图形的面积为，请直接写出的最小值与最大值（分别用含的式子表示），
（参考数据：）
【答案】(1)1,1，
(2)①是等边三角形，理由见解析；②
(3)
【分析】（1）如图1，若将三角板的顶点P放在点O处，在旋转过程中，当OF与OB重合时，OE与OC重合，此时重叠部分的面积=△OBC的面积=正方形ABCD的面积=1；当OF与BC垂直时，OE⊥BC，重叠部分的面积=正方形ABCD的面积=1；一般地，若正方形面积为S，在旋转过程中，重叠部分的面积S1与S的关系为S1=S．利用全等三角形的性质证明即可；
（2）①结论：△OMN是等边三角形．证明OM=ON，可得结论；
②如图3中，连接OC，过点O作OJ⊥BC于点J．证明△OCM≌△OCN（SAS），推出∠COM=∠CON=30°，解直角三角形求出OJ，即可解决问题；
（3）如图4-1中，过点O作OQ⊥BC于点Q，当BM=CN时，△OMN的面积最小，即S2最小．如图4-2中，当CM=CN时，S2最大．分别求解即可．
（1）
如图1，若将三角板的顶点P放在点O处，在旋转过程中，当OF与OB重合时，OE与OC重合，此时重叠部分的面积=△OBC的面积=正方形ABCD的面积=1；
当OF与BC垂直时，OE⊥BC，重叠部分的面积=正方形ABCD的面积=1；
一般地，若正方形面积为S，在旋转过程中，重叠部分的面积S1与S的关系为S1=S．
理由：如图1中，设OF交AB于点J，OE交BC于点K，过点O作OM⊥AB于点M，ON⊥BC于点N．
∵O是正方形ABCD的中心，
∴OM=ON，
∵∠OMB=∠ONB=∠B=90°，
∴四边形OMBN是矩形，
∵OM=ON，
∴四边形OMBN是正方形，
∴∠MON=∠EOF=90°，
∴∠MOJ=∠NOK，
∵∠OMJ=∠ONK=90°，
∴△OMJ≌△ONK（AAS），
∴S△PMJ=S△ONK，
∴S四边形OKBJ=S正方形OMBN=S正方形ABCD，
∴S1=S．
故答案为：1，1，S1=S．
（2）
①如图2中，结论：△OMN是等边三角形．
理由：过点O作OT⊥BC，
∵O是正方形ABCD的中心，
∴BT=CT，
∵BM=CN，
∴MT=TN，
∵OT⊥MN，
∴OM=ON，
∵∠MON=60°，
∴△MON是等边三角形；
②如图3中，连接OC，过点O作OJ⊥BC于点J．
∵CM=CN，∠OCM=∠OCN，OC=OC，
∴△OCM≌△OCN（SAS），
∴∠COM=∠CON=30°，
∴∠OMJ=∠COM+∠OCM=75°，
∵OJ⊥CB，
∴∠JOM=90°-75°=15°，
∵BJ=JC=OJ=1，
∴JM=OJ•tan15°=2-，
∴CM=CJ-MJ=1-（2-）=-1，
∴S四边形OMCN=2××CM×OJ=-1．
（3）
如图4，将沿翻折得到，则，此时则当在上时，比四边形的面积小，

设，则当最大时，最小，
，即时，最大，
此时垂直平分，即，则
如图5中，过点O作OQ⊥BC于点Q，

，
BM=CN
当BM=CN时，△OMN的面积最小，即S2最小．
在Rt△MOQ中，MQ=OQ•tan=tan，
∴MN=2MQ=2tan，
∴S2=S△OMN=×MN×OQ=tan．
如图6中，同理可得，当CM=CN时，S2最大．


则△COM≌△CON，
∴∠COM=，
∵∠COQ=45°，
∴∠MOQ=45°-，
QM=OQ•tan（45°-）=tan（45°-），
∴MC=CQ-MQ=1-tan（45°-），
∴S2=2S△CMO=2××CM×OQ=1-tan（45°-）．
【点睛】本题属于四边形综合题，考查了正方形的性质，旋转变换，全等三角形的判定和性质，四边形的面积等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．
28．（2022·辽宁鞍山·模拟预测）如图，正方形中，点，，分别为边，，上的点，且，连接，，．
(1)可以看成是绕点逆时针旋转角所得，请在图中画出点，并直接写出角的度数；
(2)当点位于何处时，的面积取得最小值？请说明你的理由；
(3)试判断直线与外接圆的位置关系，并说明你的理由．
【答案】(1)见解析
(2)当点E位于的中点时，面积取得最小值，理由见解析
(3)：当点E位于的中点时，直线与外接圆相切；当点E位于的非中点时，直线与外接圆相交．理由见解析
【分析】（1）根据正方形的性质与旋转的性质，连接交于点M，则点M即为旋转中心；
（2）先证明，得，，得到是等腰直角三角形，再根据勾股定理与三角形面积公式得到，然后利用二次函数的最值求解即可；
（3）分两种情况：当点E位于的中点时，直线与外接圆相切；当点E位于的非中点时，直线与外接圆相交．分别说明理由 即可．
【详解】（1）解：如图1，连接交于点M，则点M即为所求，
∴旋转角；
（2）解：当点E位于的中点时，面积取得最小值．
理由：设正方形的边找为a， ，则，
在和中，
，
∴，
∴，，
∴是等腰直角三角形，
∴，
∴当时，即点E位于的中点时，面积最小，
（3）解：当点E位于的中点时，直线与的外接圆相切．
理由：设的中点为O，连接，如图2，
∴，
当点E位于的中点时，点G于的中点，点F于的中点，
∴，
∴，
∴当O到的距离为，
∴直线与外接圆相切；
当点E位于的非中点时，直线与外接圆相交，
理由：当点E位于的非中点时，，
∴O到的距离
∴直线与外接圆相交．
综上当点E位于的中点时，直线与外接圆相切；当点E位于的非中点时，直线与外接圆相交．
【点睛】本踢考查正方形的性质，旋转的性质，全等三角形的判定与性质，勾股定理，切线的判定，证明是解题的关键．
29．（2022·山东枣庄·校考模拟预测）如图1，在等腰直角三角形中，，．点是的中点，以为边作正方形，连接，．将正方形绕点顺时针旋转，旋转角为（）．
(1)如图2，在旋转过程中，
①判断与是否全等，并说明理由；
②当时，与交于点，求的长．
(2)如图3，延长交直线于点．求证：；
【答案】(1)①，理由见解析；②
(2)证明见解析
【分析】（1）①根据“边角边”，证明即可；②过点作于，根据①中，，得出，再根据三线合一的性质，得出，再根据勾股定理，得出，再根据，得出，再根据相似三角形的性质，计算即可得出答案；
（2）设交于，根据（1），得出，再根据角之间的数量关系，得出，再根据等量代换，得出，再根据垂线的定义，即可得出结论．
【详解】（1）解：①如图2中，结论：．
理由：∵四边形是正方形，
∴，，
∵，，
∴，
∴，
∴．
②如图2中，过点作于．
∵，，
∴，
∵，
∴，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
∴．
（2）证明：如图3中，设交于．
∵，
∴，
∵，，
∴，
∴，
∴．
【点睛】本题考查了全等三角形的判定与性质、三线合一的性质、勾股定理、相似三角形的判定与性质、垂线的定义，解本题的关键在熟练掌握相关的性质定理．
30．（2022·山东德州·统考二模）如图，在矩形中，，，平分交于点.连接，点是上一动点，过点作交于点．将绕点旋转得到．
(1)连接，，求证：；
(2)当点恰好落在直线上时，若，求的值．
【答案】(1)见解析
(2)或
【分析】（1）先证得，，从而证明了结论；
（2）先求得的长，进而求得，然后利用勾股定理解直角三角形，即可求得结果．
【详解】（1）（1）证明：∵，
∴，
∴，
∴，
由旋转可知：，
∴，
即，
∴；
（2）如图1，
∵四边形是矩形，
∴，
∵平分，
∴，
∴，
∴，
∴，
∴，
由（1）知：，
∴，
∴，
∴，
在中，由勾股定理得，，
∴，，
综上所述，或．
【点睛】本题考查了矩形性质，相似三角形判定和性质，勾股定理等知识，解决问题的关键是作辅助线，构造相似三角形．
【考点7 特殊四边形中的动点问题】
31．（2022·四川绵阳·校考二模）在矩形中，，点是对角线上一动点（不与点重合），连接，过点作交线段于点，设．
(1)如图①，求的值（用含的代数式表示）．
(2)如图②，连接，当平分时，求的值．
【答案】(1)
(2)的值是
【分析】（1）过点P作于点M，根据矩形的性质和补角的性质可证，然后证明得出，从而求出，，，最后根据正切的定义求解即可；
（2）易得点P、E、C、B四点共圆，取的中点为圆心O，因为同弧所对的圆周角相等，所以，又因为平分，所以，即，所以，再结合（1）可得，即可解答．
【详解】（1）解：如图，过点作于点，
∵四边形为矩形，，
∴，
又∵
∴，
∵，
∴，
∵，
∴
∴，即，
∴，
∴
∴；
（2）解：如图，取的中点，连接、，
∵，
∴
∴点四点在上，
∴
∵平分，
∴，
∴，
∴，
由（1）可得，
解得，经检验：是分式方程的解．
故的值是．
【点睛】本题是四边形综合题，考查了矩形的性质、相似三角形的判定和性质、勾股定理、锐角三角函数以及四点共圆等知识；熟练掌握矩形的性质和勾股定理，证明三角形相似是解决问题的关键．
32．（2022·江苏淮安·统考一模）【图形定义】有一组邻边相等的凸四边形叫做“等邻边四边形”．
【问题探究】
(1)如图①，已知矩形是“等邻边四边形”，则矩形___________（填“一定”或“不一定”）是正方形；
(2)如图②，在菱形中，，，动点、分别在、上（不含端点），若，试判断四边形是否为“等邻边四边形”？如果是“等邻边四边形”，请证明；如果不是，请说明理由；此时，四边形的周长的最小值为___________；
【尝试应用】
(3)现有一个平行四边形材料，如图③，在中，，，，点在上，且，在边上有一点，使四边形为“等邻边四边形”，请直接写出此时四边形ABEP的面积可能为的值___________．
【答案】(1)一定
(2)四边形是“等邻边四边形”，理由见解析，四边形的周长最小值为
(3)或或14
【分析】（1）根据等邻边四边形的定义和正方形的判定可得出结论；
（2）如图②中，结论：四边形是等邻四边形，利用全等三角形的性质证明即可；
（3）如图③中，过点作于，点作于N，则四边形是矩形．分三种情形：①当时，②当时，③当时，分别求解即可．
【详解】（1）∵四边形的邻边相等，
∴矩形一定是正方形；
故答案为：一定；
（2）如图②，四边形是等邻四边形；
理由：连接．
∵四边形是菱形，
∴，，
∴，都是等边三角形，
∴ ，，
∵，
∴，
∴，
∴，，
∴四边形是等邻四边形，
∴，
∵，
∴的值最小时，四边形的周长最小，
根据垂线段最短可知，当时，的值最小，
此时，，
∴四边形的周长的最小值为．
（3）如图③中，过点作于，点作于N，则四边形是矩形．
∵，，
∴，，
∵，
∴，
①当时，
．
②当时，设，
在中，∵，
∴，
∴，
∴．
③当时，点与重合，此时．
．
综上：四边形的面积为或或14．
【点睛】本题考查了“等邻边四边形”的定义，等腰三角形的判定和性质，全等三角形的判定和性质，梯形的面积等知识，解题的关键是理解题意，学会正确寻找全等三角形解决问题，学会用分类讨论的思想思考问题．
33．（2022·山西·山西实验中学校考模拟预测）综合与实践：
问题情境：在综合与实践课上，数学老师出示了一道思考题：
如图，在正方形中，是射线上一动点，以为直角边在边的右侧作等腰直角三角形，使得，，且点恰好在射线上．
(1)如图1，当点在对角线上，点在边上时，那么与之间的数量关系是_________；
探索发现：
(2)当点在正方形外部时如图2与图3，（1）中的结论是否还成立？若成立，请利用图2进行证明；若不成立，请说明理由；
问题解决：
(3)如图4，在正方形中，，当是对角线的延长线上一动点时，连接，若，求的面积．
【答案】(1)；
(2)成立，证明见解析；
(3)．
【分析】（1）连接，根据正方形的性质和是等腰直角三角形，证得，可得，即可；
（2）连接，根据正方形的性质和是等腰直角三角形，证得，可得，即可；
（3）连接交于点，过点作交直线于点，根据正方形的性质，可得，再证得，可得，，在中，根据勾股定理可得，即可．
【详解】（1）解：如图，连接，
∵四边形是正方形，
∴，，
∴，
∴，
∵是等腰直角三角形，
∴，
∴，
∴，
∴，
∴，
∴．
即；
故答案为：；
（2）解：（1）中的结论还成立，证明如下：
如图2，连接，
∵四边形是正方形，
∴，，
∴，
∴，
∵是等腰直角三角形，
∴，
∴，
∴，
∴，
∴，
∴．
即；
（3）解：如图4，连接交于点，过点作交直线于点，
∵四边形是正方形，，
∴，，，
∴，，
∴，，
∴，
∴，
在中，，，
∴，
∴，
∵，
∴，
∴，
∴，，
在中，由勾股定理得，，
设，
∴，
解得，，（舍去），
即，
∴．
【点睛】本题是四边形综合题，考查了全等三角形的判定与性质，相似三角形的判定与性质，等腰直角三角形的性质，正方形的性质，勾股定理，熟练掌握正方形的性质是解题的关键．
34．（2022·广东东莞·东莞市光明中学校考三模）中，，，点为直线上一动点点不与，重合，以为边在右侧作菱形，使，连接．
(1)观察猜想：如图，当点在线段上时，
与的位置关系为：______．
，，之间的数量关系为：______；
(2)数学思考：如图，当点在线段的延长线上时，结论，是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．
(3)拓展延伸：如图，当点在线段的延长线上时，设与相交于点，若已知，，求的长．
【答案】(1)①；②
(2)①成立，证明见解析；②不成立，证明见解析
(3)
【分析】根据菱形的性质以及等边三角形的性质，推出≌，根据全等三角形的性质即可得到结论；根据全等三角形的性质得到，再根据，即可得出；
依据≌，即可得到，进而得到；依据≌可得，依据，即可得出；
判定≌，即可得到，，再根据∽，即可得到，进而得出的长．
（1）
解：，，
是等边三角形，
，
，
又菱形中，，
≌，
，
又，
，
；
≌
，
又，
，
故答案为：；；
（2）
结论成立，而结论不成立．
证明：如图，，，
是等边三角形，
，，
，
又菱形中，，
≌，
，
又，
，
；
≌
，
又，
；
（3）
解：如图，连接，过作于，则，，
中，，
，，
是等边三角形，
又，，
，
≌，
，，
又，
∽，
，
可设，则，，，
，
解得，
．
【点睛】此题属于四边形综合题，主要考查了全等三角形的判定和性质，菱形的性质，等边三角形的判定和性质，相似三角形的判定和性质的综合运用，利用已知条件判定≌和∽是解本题的关键．
35.（2022·浙江绍兴·统考中考真题）如图，在矩形中，，，动点从点出发，沿边，向点运动，，关于直线的对称点分别为，，连结．
(1)如图，当在边上且时，求的度数．
(2)当在延长线上时，求的长，并判断直线与直线的位置关系，说明理由．
(3)当直线恰好经过点时，求的长．
【答案】(1)∠AEM＝90°；
(2)DE＝；MN∥BD，证明见解析；
(3)DE的长为或．
【分析】（1）由DE＝2知，AE＝AB＝6，可知∠AEB＝∠MEB＝45°，从而得出答案；
（2）根据对称性得，∠ENC＝∠BDC，则cs∠ENC＝，得EN＝，利用SSS证明△BMN≌△DCB，得∠DBC＝∠BNM，则MN∥BD；
（3）当点E在边AD上时，若直线MN过点C，利用AAS证明△BCM≌△CED，得DE＝MC；当点E在边CD上时，证明△BMC∽△CNE，可得，从而解决问题．
【详解】（1）解：∵DE=2，
∴AE＝AB＝6，
∵四边形ABCD是矩形，
∴∠A＝90°，
∴∠AEB＝∠ABE＝45°，
由对称性知∠BEM＝45°，
∴∠AEM=∠AEB+∠BEM＝90°；
（2）如图1，
∵AB=6，AD=8，
∴由勾股定理得BD=10，
∵当N落在BC延长线上时，BN＝BD＝10，
∴CN＝2．
由对称性得，∠ENC＝∠BDC，
∴cs∠ENC＝，
∴EN＝，
∴DE＝EN＝；
直线MN与直线BD的位置关系是MN∥BD．
由对称性知BM＝AB＝CD，MN＝AD＝BC，
又∵BN＝BD，
∴△BMN≌△DCB（SSS），
∴∠DBC＝∠BNM，
所以MN∥BD；
（3）①情况1：如图2，当E在边AD上时，直线MN过点C，
∴∠BMC＝90°，
∴MC＝．
∵BM＝AB＝CD，∠DEC＝∠BCE，∠BMC＝∠EDC＝90°，
∴△BCM≌△CED（AAS），
∴DE＝MC＝；
②情况2：如图3，点E在边CD上时，
∵BM＝6，BC＝8，
∴MC＝，CN＝8-，
∵∠BMC＝∠CNE＝∠BCD＝90°，
∴∠BCM＋∠ECN＝90°，
∵∠BCM＋∠MBC＝90°，
∴∠ECN＝∠MBC，
∴△BMC∽△CNE，
∴，
∴EN，
∴DE＝EN＝．
综上所述，DE的长为或．
【点睛】本题是四边形综合题，主要考查了矩形的性质，轴对称的性质，全等三角形的判定与性质，相似三角形的判定与性质，三角函数等知识，根据题意画出图形，并运用分类讨论思想是解题的关键．
【考点8 中点四边形的形状探究】
36.（2022·湖南张家界·统考二模）如图，E、F、G、H分别是四边形ABCD边AB、BC、CD、AD的中点，下列说法正确的是（ ）
A．当AC⊥BD时，四边形EFGH是菱形
B．当AC＝BD时，四边形EFGH是矩形
C．当四边形ABCD是平行四边形时，则四边形EFGH是矩形
D．当四边形ABCD是矩形时，则四边形EFGH是菱形
【答案】D
【分析】根据中位线的性质可得EH=FG=BD，EF=GH=AC，EH//FG//BD，EF//GH//AC，可得四边形EFGH是平行四边形，根据菱形、矩形的判定定理逐一判断即可得答案．
【详解】∵E、F、G、H分别是四边形ABCD边AB、BC、CD、AD的中点，
∴EH=FG=BD，EF=GH=AC，EH//FG//BD，EF//GH//AC，
∴四边形EFGH是平行四边形，
当AC⊥BD，∠EFG=90°，
∴四边形EFGH是矩形，故A选项错误，
当AC＝BD时，EH=FG=EF=GH，
∴四边形EFGH是菱形，故B选项错误，
当四边形ABCD是平行四边形时，四边形EFGH是平行四边形，故C选项错误，
当四边形ABCD是矩形时，AC=BD，则四边形EFGH是菱形，故D选项正确
故选：D．
【点睛】本题考查中点四边形、平行四边形、矩形、菱形的判定等知识，解题的关键是记住一般四边形的中点四边形是平行四边形，当对角线BD=AC时，中点四边形是菱形，当对角线AC⊥BD时，中点四边形是矩形，当对角线AC=BD，且AC⊥BD时，中点四边形是正方形．
37．（2022·上海黄浦·格致中学校考二模）顺次连结等腰梯形各边中点得到的四边形是（ ）
A．矩形B．菱形C．等腰梯形D．平行四边形
【答案】B
【分析】连接AC、BD，可证MN为△ABD的中位线，PQ为△CBD的中位线，根据中位线定理可证MN∥BD∥PQ，MN=PQ=BD，同理可证PN∥AC∥MQ，NP=MQ=AC，根据等腰梯形的性质可知AC=BD，故可证四边形PQMN为菱形．
【详解】解：连接AC、BD，
∵M、N分别为AD、AB的中点，
∴MN为△ABD的中位线，
∴MN∥BD，MN=BD，
同理可证BD∥PQ，PQ=BD，
∴MN=PQ，MN∥PQ，四边形PQMN为平行四边形，
同理可证NP=MQ=AC，
根据等腰梯形的性质可知AC=BD，
∴PQ=NP，
∴平行四边形PQMN为菱形．
故选：B．
【点睛】本题主要考查等腰梯形的性质在证明特殊平行四边形中的应用．同时运用了三角形的中位线定理．
38.（2022·内蒙古呼伦贝尔·统考二模）若顺次连接四边形ABCD各边的中点所得四边形是菱形．则四边形ABCD一定是 ( )
A．菱形B．对角线互相垂直的四边形
C．矩形D．对角线相等的四边形
【答案】D
【分析】根据三角形的中位线定理得到EH∥FG，EF=FG，EF=BD，要是四边形为菱形，得出EF=EH，即可得到答案．
【详解】解：∵E，F，G，H分别是边AD，AB，CB，DC的中点，
∴EH=AC，EH∥AC，FG=AC，FG∥AC，EF=BD，
∴EH∥FG，EF=FG，
∴四边形EFGH是平行四边形，
假设AC=BD，
∵EH=AC，EF=BD，
则EF=EH，
∴平行四边形EFGH是菱形，
即只有具备AC=BD即可推出四边形是菱形，
故选：D．
【点睛】题目主要考查中位线的性质及菱形的判定和性质，理解题意，熟练掌握运用三角形中位线的性质是解题关键．
39．（2022·四川达州·四川省渠县中学校考二模）如图，任意四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，对于四边形EFGH的形状，某班学生在一次数学活动课中，通过动手实践，探索出如下结论，其中错误的是（ ）
A．当E，F，G，H是各边中点，且AC=BD时，四边形EFGH为菱形
B．当E，F，G，H是各边中点，且AC⊥BD时，四边形EFGH为矩形
C．当E，F，G，H不是各边中点时，四边形EFGH可以为平行四边形
D．当E，F，G，H不是各边中点时，四边形EFGH不可能为菱形
【答案】D
【分析】根据连接四边形各边中点所得的四边形必为平行四边形，根据中点四边形的性质进行判断，即可求解
【详解】解：A．当E，F，G，H是各边中点，且AC=BD时，EF=FG=GH=HE，故四边形EFGH为菱形，故A正确；
B．当E，F，G，H是各边中点，且AC⊥BD时，∠EFG=∠FGH=∠GHE=90°，故四边形EFGH为矩形，故B正确；
C．当E，F，G，H不是各边中点时，EF∥HG，EF=HG，故四边形EFGH为平行四边形，故C正确；
D．当E，F，G，H不是各边中点时，四边形EFGH可能为菱形，故D错误；
故选D．
40．（2022·江苏淮安·统考一模）如图1，在四边形中，如果对角线和相交并且相等，那么我们把这样的四边形称为等角线四边形．
(1)①在“平行四边形、矩形、菱形”中， 一定是等角线四边形（填写图形名称）；
②若、、、分别是等角线四边形四边、、、的中点，当对角线、还要满足 时，四边形是正方形．
(2)如图2，已知中，，，，为平面内一点．
①若四边形是等角线四边形，且，求四边形的面积；
②设点是以为圆心，为半径的圆上的动点，若四边形是等角线四边形，则四边形的面积的最大值为 ．
【答案】(1)①矩形；②
(2)①；②
【分析】（1）①根据等角线四边形的定义进行判断即可；
②当时，四边形是正方形，首先证明四边形是菱形，再证明有一个角是直角即可；
（2）①如图2中，作于，利用勾股定理求出相关线段的长，再根据计算即可；
②如图3中，设与相交于点，连接，只要证明当且、、共线时，四边形的面积最大即可．
【详解】（1）解：①在“平行四边形、矩形、菱形”中，
∵矩形的对角线相等，
∴矩形一定是等角线四边形．
故答案为：矩形．
②当时，四边形是正方形．理由如下：
如图1，∵、、、分别是等角线四边形四边、、、的中点，
∴，，，，，，
∵，
∴，
∴四边形是菱形，
∵，
∴，
∵，，
∴，，
∴，
∴四边形是正方形．
故答案为：．
（2）①如图2，作于，
∵在中，，，，
∴，
∵，，
∴，
∵四边形是等角线四边形，
∴，
在中，，
∴
．
∴四边形的面积为．
②如图3中，设与相交于点，连接，作于，于，
∴，，
∵四边形是等角线四边形，
∴，
∵
，
即：，
∴当点与点重合时即，等号成立，
∵，
∴，
即线段最长时，四边形的面积最大，
∵，
∴，
∴，
∴的最大值为，
∴当、、共线时，四边形的面积的最大值为．
故答案为：18．
【点睛】本题考查四边形综合题，考查了中点四边形，三角形中位线定理，正方形的判定，勾股定理，等腰三角形的三线合一性质，垂线段最短，三角形三边关系定理，圆等知识．解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，会求圆上一点到圆外一定点的距离的最大值或最小值．
【考点9 中点四边形的线段长、周长与面积的探究】
41.（2022·山东枣庄·校考一模）如图，在中，，点是斜边的中点，分别以点，为圆心，以的长为半径画弧，两弧交于点，连接，，得到四边形，依次连接四边形四条边中点得到四边形，若，那么四边形的周长为（ ）
A．B．C．D．
【答案】B
【分析】在Rt△ABC中，∠CAB=90°，AC=2，∠C=60°，推出BC=2AC=4，AB=AC=2,由BD=CD，推出AD=DB=DC=2，由作图可知，四边形ADBE是菱形，推出中点四边形GHIJ是矩形，求出IJ．IH，即可解决问题．
【详解】解：在Rt△ABC中，∠CAB=90°，AC=2，∠C=60°，
∴BC=2AC=4，AB =AC=2
∵BD=CD，
∴AD=DB=DC=2，
由作图可知，四边形ADBE是菱形，
∴中点四边形GHIJ是矩形，
∵AD=AC=DC，
∴∠ADC=60°，
∵AE∥DB，
∴∠EAD=∠ADC=60°，
∵AE=AD，
∴△AED是等边三角形，
∴AD=DE=2，
∵AJ=JE，AI=ID，
∴IJ= DE=1,
∵BH=DH，AI=ID，
∴IH=AB =
∴四边形GHIJ的周长=2（1+ ）=2+2
故选：B．
【点睛】本题考查中点四边形，解直角三角形，菱形的判定和性质，三角形中位线定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
42．（2022·辽宁沈阳·沈阳市第七中学校考模拟预测）如图，在四边形中，，点，，，分别是，，，的中点，若，，则四边形的面积是______．
【答案】12
【分析】根据三角形中位线定理、矩形的判定定理得到四边形为矩形，根据矩形的面积公式计算，得到答案．
【详解】解：∵点，，，分别是，，，的中点，
∴， ，，，， ，
∴，，
∴四边形为平行四边形，
，
∴，
∴平行四边形为矩形，
∴，
故答案为：．
【点睛】此题考查了中点四边形，解题的关键是掌握三角形中位线定理、矩形的判定定理．
43.（2022·山东济南·模拟预测）如图，在四边形ABCD中，AC=BD，E、F、G、H分别是AB、BC、CD、DA的中点，且EG、FH交于点O．若AC=4，则EG2+FH2=______．
【答案】16
【分析】根据三角形的中位线定理和菱形的判定，可得顺次连接对角线相等的四边形各边中点所得四边形是菱形；根据菱形的性质得到EG⊥HF，且EG=2OE，FH=2OH．在Rt△OEH中，根据勾股定理得到OE2+OH2=EH2=4，再根据等式的性质，在等式的两边同时乘以4，根据4=22，把等式进行变形，并把EG=2OE，FH=2OH代入变形后的等式中，即可求出EG2+FH2的值．
【详解】∵E、F、G、H分别是线段AB、BC、CD、AD的中点，
∴EH、FG分别是△ABD、△BCD的中位线，
EF、HG分别是△ABC、△ACD的中位线，
根据三角形的中位线的性质知，EH=FGBD，EF=HGAC．
又∵AC=BD，
∴EH=FG=EF=HG，
∴四边形EFGH是菱形，
∴EG⊥FH，EG=2OE，FH=2OH．
在Rt△OEH中，根据勾股定理得：OE2+OH2=EH2=4，
等式两边同时乘以4得：4OE2+4OH2=4×4=16，
∴（2OE）2+（2OH）2=16，
即EG2+FH2=16．
故答案为16．
【点睛】本题考查了三角形中位线定理和菱形的判定方法，题目比较典型，又有综合性，难度不大．
44．（2022春·陕西西安·八年级陕西师大附中校考期末）问题背景：
△ABC和△CDE均为等边三角形，且边长分别为a，b，点D，E分别在边AC，BC上，点F，G，H，I分别为AB，BE，ED，AD的中点，连接FG，GH，HI，IF
猜想证明：
(1)如图①，判断四边形FGHI是什么特殊四边形，并说明理由．
(2)当a＝6，b＝2时，求四边形FGHI的周长．
拓展延伸：
(3)如图②，当四边形FGHI是正方形时，连接AE，BD相交于点N，点N，H恰好在FC上．求证：△ABN和△DEN均为等腰直角三角形．
【答案】(1)四边形FGHI是菱形．理由见解析
(2)四边形FGHI的周长为
(3)见解析
【分析】（1）根据△ABC和△CDE为等边三角形，可得四边形ABED是等腰梯形，再根据点F，G，H，I分别为AB，BE，ED，AD的中点，即可得出FG=IH=FI=GH，进而得到四边形FGHI是菱形；
（2）过A作AM⊥BC于M，连接AE，再根据勾股定理，求得Rt△ACM中，AM=3，Rt△AEM中，AE=2，由（1）可得，四边形FGHI是菱形，且AE=2FG，即可得出四边形FGHI的周长=4FG=2AE；
（3）由点F为AB的中点，△ABC和△CDE均为等边三角形，所以直线CF为△ABC和△CDE的对称轴，则有AN＝BN，DN＝EN，再利用三角形中位线得FGAEIH，FIBDGH，则FGAEIH，FIBDGH，又由四边形FGHI是正方形，得∠FNA＝∠FHI＝45°，∠FNB＝∠FHG＝45°，即可得∠ANB＝∠FNA+∠FNB＝90°，∠DNE＝90°，即可得出结论．
【详解】（1）解：四边形FGHI是菱形.
理由：如图①，连接AE,BD，
∵△ABC和△CDE均为等边三角形，
∴AC＝BC,EC＝DC，
在△AEC和△BDC中，
，
∴△AEC≌△BDC(SAS)，
∴AE＝BD，
∵点F，G，H，I分别为AB，BE，ED，AD的中点，
FG＝AE＝IH.FI＝BD＝CH.
∴FG＝GH＝IH＝FI.
∴四边形FGHI是菱形；
（2）解：如图②，过点D作DM⊥EC于点M，
∵△CDE为等边三角形，
∴MC＝EC＝×2＝1，∠C＝60°，
∴BM＝BC－MC＝6－1＝5，
在Rt△DMC中，DM＝，
在Rt△BDM中，BD＝，
∴GH＝BD＝，
由(1)知四边形FGHI是菱形，
∴.四边形FGHI的周长为4GH＝4.
（3）解：∵点F为AB的中点，△ABC和△CDE均为等边三角形，
∴直线CF为△ABC和△CDE的对称轴.
∴AN＝BN，DN＝EN，
∵点F，G，H，I分别为AB，BE，ED，AD的中点，
∴FGAE，IHAE，FIBD，GHBD.
∴.FGAEIH，FIBDGH，
∵四边形FGHI是正方形，
∴∠FNA＝∠FHI＝45°，∠FNB＝∠FHG＝45°
∴.∠ANB＝∠FNA+∠FNB＝90°，∠DNE＝90°.
∴△ABN和△DEN均为等腰直角三角形.
【点睛】本题属于四边形综合题，主要考查了菱形的判定，正方形的性质，中点四边形，三角形中位线定理，勾股定理的综合应用，解决问题的关键是依据三角形中位线定理．
45．（2022春·山西临汾·八年级统考期中）综合与探究：如图1，四边形中，、、、分别是、、、的中点，顺次连接、、、．
(1)猜想四边形的形状是________（直接回答，不必说明理由）．
(2)如图2，在四边形内一点，使，，，其他条件不变，试探究四边形的形状，并说明理由．
(3)在（2）的条件下，，，，，求四边形的面积．
【答案】(1)平行四边形
(2)菱形，见解析
(3)
【分析】(1)连接AD，利用三角形中位线定理，证明EH=FG，且EH∥FG即可得证．
(2)连接AD，BC，证明，得到AD=CB，结合三角形中位线定理，得到四边形EFGH的四边相等，即可得到菱形EFGH．
(3)连接AD，BC，交点为M，设BC与EH的交点为Q，AD与EF的交点为O，证明，判定四边形EOMQ是平行四边形，证明∠HEF=60°，连接，过点作，垂足为，求得EH，HN的长度即可．
【详解】（1）平行四边形．理由如下：
如图1，连接AD，
∵、、、分别是、、、的中点，
∴EH∥AD，EH=，FG∥AD，FG=，
∴EH=FG，且EH∥FG，
∴四边形EFGH是平行四边形，
故答案为：平行四边形．
（2）菱形.理由：如图2，连接，.
∵，
∴，
即.
又∵，，
∴，
∴.
∵、、、分别是、、、的中点，
∴、、、分别是、、、的中位线，
∴，，，，
∴，
∴四边形是菱形.
（3）连接AD，BC，交点为M，设BC与EH的交点为Q，AD与EF的交点为O，
∵，，
∴是等边三角形.
∵是中点，
∴平分，，
∴，点、、共线.
在中，，
在中，，
∴.
∵，
∴，
∴.
∵，，
∴四边形EOMQ是平行四边形，
∴.
在中，，，
∴菱形的面积.
【点睛】本题考查了三角形中位线定理，三角形全等的判定和性质，平行四边形的判定和性质，菱形的判定和性质，等边三角形的判定和性质，熟练掌握菱形的判定和性质，灵活运用三角形中位线定理是解题的关键．
【考点10 特殊四边形与函数的综合探究】
46．（2022·辽宁盘锦·统考中考真题）如图，四边形ABCD是菱形，BC＝2，∠ABC＝60°，对角线AC与BD相交于点O，线段BD沿射线AD方向平移，平移后的线段记为PQ，射线PQ与射线AC交于点M，连结PC，设OM长为，△PMC面积为．下列图象能正确反映出与的函数关系的是（ ）
A．B．C．D．
【答案】D
【分析】由四边形ABCD是菱形，BC＝2，∠ABC＝60°，可求出AC、AO、OC的长，再设OM＝x，利用解直角三角形表示出PM，分点M在线段OC上（不含点O）时和当点在线段OC延长线上时两种情况分别表示出y再结合函数图象即可判断出正确答案．
【详解】解：∵四边形ABCD是菱形，
∴AD＝BC＝2，∠BAD＝180°−∠ABC＝120°，
∴∠DAO＝∠BAD＝60°，
∴△DAC是等边三角形，
∴AD＝AC＝2，
∴AO＝CO＝AC＝1，
设OM＝x，
∵AC⊥BD，PQ为BD平移而来，
∴∠AOD＝∠AMP＝90°，
∴△AMP为直角三角形，
∴PM＝AM•tan∠PAM＝（1＋x），
①当点M在线段OC上（不含点O）时，
即0≤x＜1，此时CM＝1−x，
则y＝（1−x）×（1＋x）＝−，
∴0≤x＜1，函数图象开口应朝下，
故B、C不符合题意，
②当点在线段OC延长线上时，即x＞1，如图所示：
此时C＝x−1，
则y＝（x−1）×(x＋1)＝，
∴只有D选项符合题意，
故选：D．
【点睛】本题考查了菱形的性质，三角形面积，解直角三角形，二次函数图象等知识，熟练掌握上述知识并能分点M在线段OC上（不含点O）时和当点在线段OC延长线上时两种情况分别表示出y再结合函数图象进行判断是解题的关键．
47．（2022·内蒙古·统考中考真题）如图，在平面直角坐标系中，矩形OABC的OA边在x轴的正半轴上，OC边在y轴的正半轴上，点B的坐标为（4，2），反比例函数的图象与BC交于点D，与对角线OB交于点E，与AB交于点F，连接OD，DE，EF，DF．下列结论：①；②；③；④．其中正确的结论有（ ）
A．4个B．3个C．2个D．1个
【答案】A
【分析】根据题意，图中各点的坐标均可以求出来，，，只需证明即可证明结论①；先求出直线OB的解析式，然后求直线OB与反比例函数的交点坐标，即可证明结论②；分别求出和，进行比较即可证明结论③；只需证明，即可求证结论④．
【详解】解：∵OABC为矩形，点B的坐标为（4，2），
∴A点坐标为(4，0)，C点坐标为(0，2)，
根据反比例函数，
当时，，即D点坐标为(1，2)，
当时，，即F点坐标为(4，)，
∵，
∴，
∵，
∴，
∴，
，
∴，
故结论①正确；
设直线OB的函数解析式为：，
点B代入则有：，
解得：，
故直线OB的函数解析式为：，
当时，(舍)
即时，，
∴点E的坐标为(2，1)，
∴点E为OB的中点，
∴，
故结论②正确；
∵，
∴，
由②得：，
，
∴，
故结论③正确；
在和中，
，
∴，
∴，
故结论④正确，
综上：①②③④均正确，
故选：A．
【点睛】本题主要考查矩形的性质，相似三角形判定与性质，锐角三角函数，反比例函数与几何综合，结合题意求出图中各点坐标是解决本题的关键．
48．（2022·新疆·统考中考真题）如图，在巾，，点O为BC的中点，点D是线段OC上的动点（点D不与点O，C重合），将沿AD折叠得到，连接BE．
(1)当时，___________；
(2)探究与之间的数量关系，并给出证明；
(3)设，的面积为x，以AD为边长的正方形的面积为y，求y关于x的函数解析式．
【答案】(1)
(2)
(3)
【分析】（1）首先由折叠的性质可得，再由等腰三角形的性质可求解；
（2）首先由折叠的性质可得，，再由等腰三角形的性质可得，，最后根据角度关系即可求解；
（3）首先由等腰直角三角形的性质和直角三角形的性质可求的长，由勾股定理可求的长，最后根据面积和差关系可求解．
【详解】（1），，，
，
将沿折叠得到，
，
，
∴△ABE是等边三角形，
，
故答案为：60；
（2），理由如下：
将沿折叠得到，
，，
，，
，
，
，
；
（3）如图，连接，
，点是的中点，
，
，，
，，
，
，
，
，
．
【点睛】本题考查了等腰直角三角形的性质，直角三角形的性质，折叠的性质等知识，解题的关键是熟练掌握相关性质并能够灵活运用．
49．（2022秋·山西·九年级校联考期末）综合与探究
如图，抛物线与x轴交于，两点，与y轴交于点C．点是x轴上的一个动点，过点P作直线轴，与直线BC交于点M，与抛物线交于点N．
(1)求这个抛物线的函数表达式．
(2)①若点P在线段OB上运动，求线段MN的最大值；
②若点P在x轴的正半轴上运动，在y轴上是否存在点Q，使以M，N，C，Q为顶点的四边形为菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
【答案】(1)
(2)①的最大值为；②存在这样的Q点，Q点的坐标为 或或
【分析】（1）将A、B点的坐标代入函数解析式，即可求出b、c的值，从而求出函数解析式．
（2）①，先求出过的直线的解析式为的长度为，的长度为二次函数当时，的值的绝对值，可以得出关于的二次函数解析式，求出这个函数的最大值即可求解．
②组成菱形时，分三种情况，第一种情况，当作为菱形对角线；第二种情况，当作为菱形的一条边时；第三种情况，当作为菱形的一条边且P在B点右侧时，如下图:
第一种情况，对角线，因为的斜率为1，，而菱形的对角线平分角，可得到，所以菱形为正方形，N点纵坐标与C点纵坐标相同，即可求解m的值，然后可以求出Q点坐标;
第二种情况，当作为菱形的一条边时，有，联立出关于m的方程，求解即可得到答案;
第三种情况，当P在B点右侧时，只能是菱形的边，同样有，可以联立出关于m的方程，求解即可得到答案．

【详解】（1）解：把代入中，得

解得
∴．
（2）解：①设直线的表达式为，把，代入．
得，解这个方程组，得
∴．
∵点是x轴上的一动点，且轴．
∴．
∴
．
∵P在上运动，
∴当时，有最大值．
②第一种情况，对角线，因为的斜率为1，，而菱形的对角线平分角，可得到，所以菱形为正方形；
则此时点N的纵坐标为，有
解得或(舍去)，
则，
，
∴Q
第二种情况：当作为菱形的一条边时，有
，，
所以
解得或0(舍去)，
∴
∴此时Q点坐标为．
第三种情况：当P在B点右侧时，如下图，有，
，，
∴，解得或0(舍去)，
∴
∴
此时Q点的坐标为：
综上所述，点Q的坐标为或或．
【点睛】本题考查了二次函数的综合运用、二次函数性质、待定系数法、一次函数的性质、菱形的性质和判定等知识，解题的关键是会构建二次函数解决最值问题，并用分类讨论的思想思考问题．
50.（2022·广西·中考真题）已知抛物线经过A（－1，0）、B（0、3）、 C（3，0）三点，O为坐标原点，抛物线交正方形OBDC的边BD于点E，点M为射线BD上一动点，连接OM ，交BC于点F
(1)求抛物线的表达式；
(2)求证：∠BOF＝∠BDF ：
(3)是否存在点M使△MDF为等腰三角形？若不存在，请说明理由；若存在，求ME的长
【答案】(1)
(2)见解析
(3)存在，或
【分析】（1）设抛物线的表达式为，将A（－1，0）、B（0、3）、C（3，0）代入，直接利用待定系数法求解即可；
（2）由正方形的性质可得，即可证明，根据全等三角形的性质即可求证；
（3）分别讨论：当点M在线段BD的延长线上时，当点M在线段BD上时，依次用代数法和几何法求解即可．
（1）
设抛物线的表达式为，
将A（－1，0）、B（0、3）、C（3，0）代入，
得，解得，
抛物线的表达式为；
（2）
四边形OBDC是正方形，
，
，
，
；
（3）
存在，理由如下：
当点M在线段BD的延长线上时，此时，
，
设，
设直线OM的解析式为，
，
解得，
直线OM的解析式为，
设直线BC的解析式为，
把B（0、3）、 C（3，0）代入，得，
解得，
直线BC的解析式为，
令，解得，则，
，
四边形OBDC是正方形，
，
，
，
，
，
解得或或，
点M为射线BD上一动点，
，
，
，
当时，解得或，
，
．
当点M在线段BD上时，此时，，
，
，
，
由（2）得，
四边形OBDC是正方形，
，
，
，
，
，
，
，
，
；
综上，ME的长为或．
【点睛】本题考查了待定系数法求二次函数解析式，求一次函数解析式，正方形的性质，全等三角形的判定和性质，解直角三角形等，熟练掌握知识点是解题的关键．图形名称
基本图的个数
特征图形的个数
图1
1
5
图2
2
9
图3
3
13
图4
4
______
…
…
…