中考数学一轮复习专题12 二次函数的图象及性质（10个高频考点）（举一反三）（2份，原卷版+解析版）

这是一份中考数学一轮复习专题12 二次函数的图象及性质（10个高频考点）（举一反三）（2份，原卷版+解析版），文件包含中考数学一轮复习专题12二次函数的图象及性质10个高频考点举一反三原卷版doc、中考数学一轮复习专题12二次函数的图象及性质10个高频考点举一反三解析版doc等2份试卷配套教学资源，其中试卷共104页， 欢迎下载使用。
TOC \ "1-1" \h \u
\l "_Tc12615" 【考点1 二次函数的定义】 PAGEREF _Tc12615 \h 1
\l "_Tc9986" 【考点2 二次函数的图象与性质】 PAGEREF _Tc9986 \h 2
\l "_Tc14120" 【考点3 二次函数的图象与系数的关系】 PAGEREF _Tc14120 \h 3
\l "_Tc26148" 【考点4 二次函数的对称性】 PAGEREF _Tc26148 \h 5
\l "_Tc24726" 【考点5 二次函数的最值】 PAGEREF _Tc24726 \h 6
\l "_Tc10747" 【考点6 待定系数法求二次函数的解析式】 PAGEREF _Tc10747 \h 7
\l "_Tc30411" 【考点7 二次函数图象的平移】 PAGEREF _Tc30411 \h 10
\l "_Tc23504" 【考点8 二次函数与一元二次方程】 PAGEREF _Tc23504 \h 12
\l "_Tc14103" 【考点9 利用二次函数的图象确定一元二次方程的近似根】 PAGEREF _Tc14103 \h 14
\l "_Tc48" 【考点10 二次函数与不等式】 PAGEREF _Tc48 \h 16
【要点1 二次函数的概念】
一般地，形如y=+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数．其中x、y是变量，a、b、c
是常量，a是二次项系数，b是一次项系数，c是常数项．y=+bx+c（a、b、c是常数，a≠0）也叫做二
次函数的一般形式．
【考点1 二次函数的定义】
【例1】（2022·安徽合肥·校考一模）已知是关于x的二次函数，那么m的值为______
【变式1-1】（2022·湖南怀化·中考真题）下列函数是二次函数的是（ ）
A．B．C．D．
【变式1-2】（2022·重庆永川·统考一模）某长方体木块的底面是正方形，它的高比底面边长还多50cm，把这个长方体表面涂满油漆时，如果每平方米费用为16元，那么总费用与底面边长满足的函数关系是（ ）
A．正比例函数关系B．一次函数关系
C．反比例函数关系D．二次函数关系
【变式1-3】（2022·江苏徐州·统考一模）请选择一组你喜欢的、、的值，使二次函数的图象同时满足下列条件：①开口向下；②当时，随的增大而增大；当时，随的增大而减小．这样的二次函数的解析式可以是________．
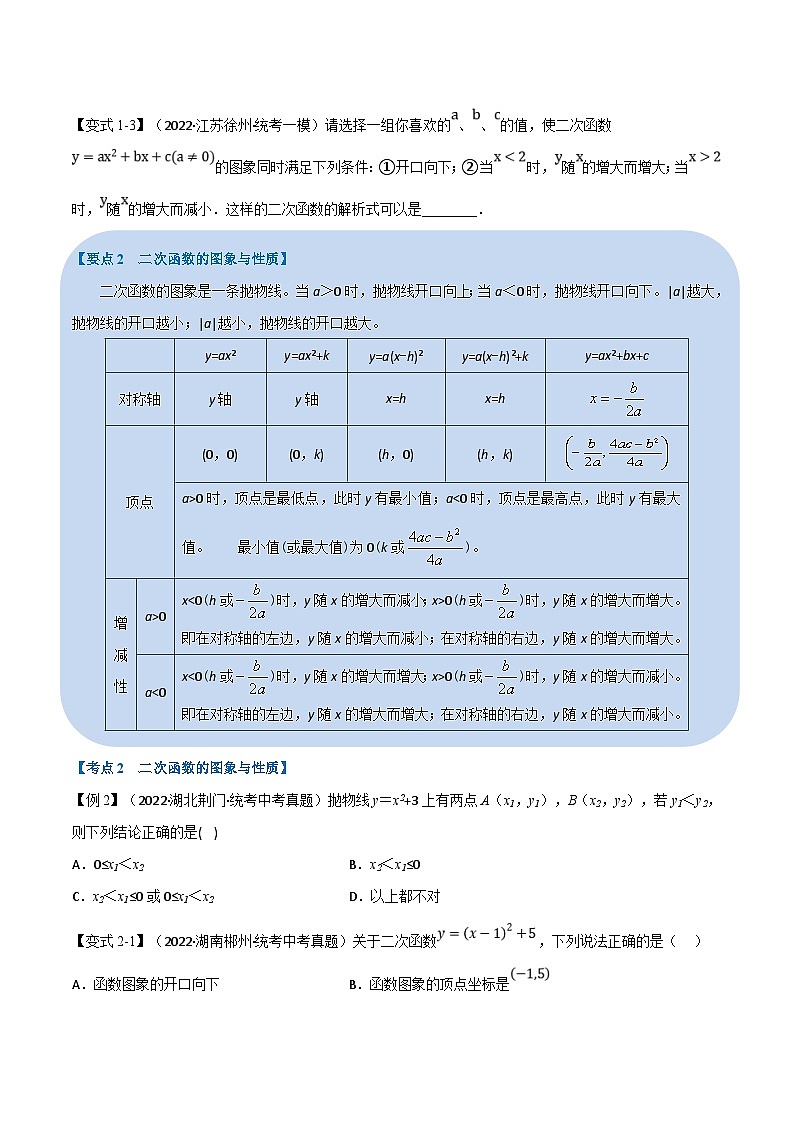
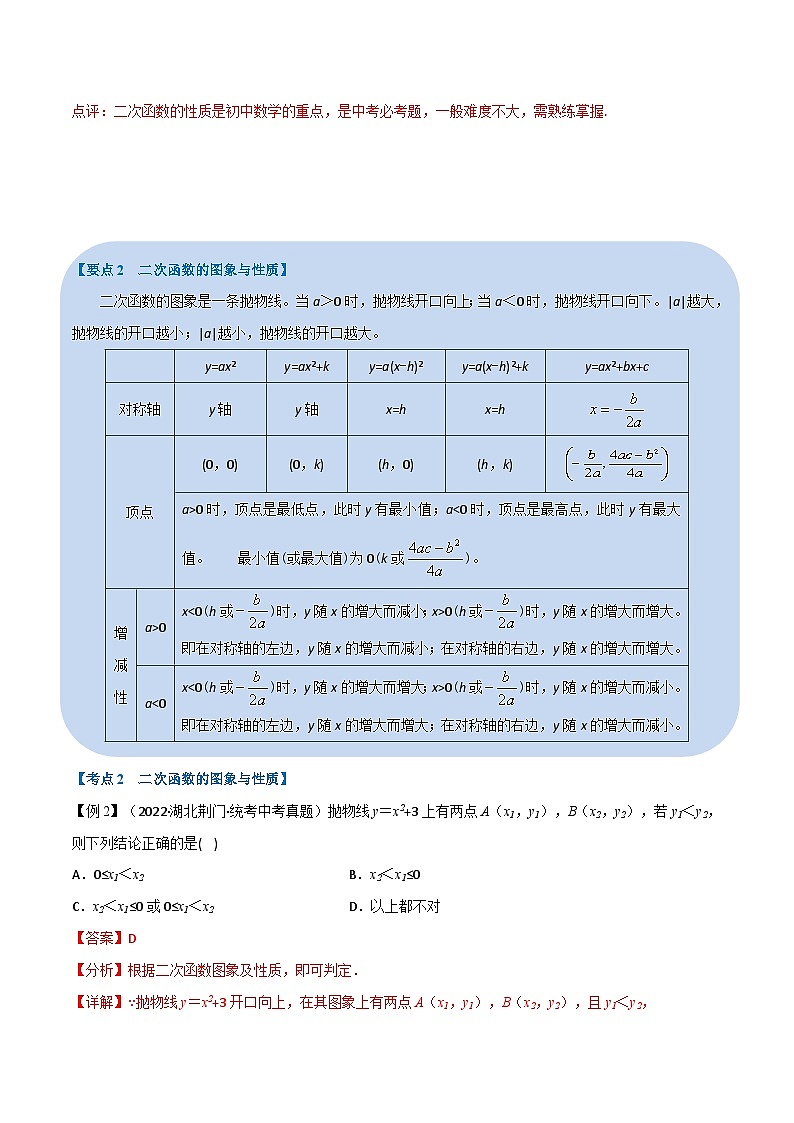
【要点2 二次函数的图象与性质】
二次函数的图象是一条抛物线。当a＞0时，抛物线开口向上；当a＜0时，抛物线开口向下。|a|越大，抛物线的开口越小；|a|越小，抛物线的开口越大。
【考点2 二次函数的图象与性质】
【例2】（2022·湖北荆门·统考中考真题）抛物线y＝x2+3上有两点A（x1，y1），B（x2，y2），若y1＜y2，则下列结论正确的是( )
A．0≤x1＜x2B．x2＜x1≤0
C．x2＜x1≤0或0≤x1＜x2D．以上都不对
【变式2-1】（2022·湖南郴州·统考中考真题）关于二次函数，下列说法正确的是（ ）
A．函数图象的开口向下B．函数图象的顶点坐标是
C．该函数有最大值，是大值是5D．当时，y随x的增大而增大
【变式2-2】（2022·青海西宁·统考中考真题）如图，△ABC中，BC=6，BC边上的高为3，点D，E，F分别在边BC，AB，AC上，且EF∥BC．设点E到BC的距离为x，△DEF的面积为y，则y关于x的函数图象大致是（ ）
A．B．
C．D．
【变式2-3】（2022·江苏盐城·统考中考真题）若点在二次函数的图象上，且点到轴的距离小于2，则的取值范围是____________．
【要点3 二次函数的图象与各系数之间的关系】
① 二次项系数：总结起来，决定了抛物线开口的大小和方向，的正负决定开口方向，的大小决定开口的大小．
②一次项系数：在确定的前提下，决定了抛物线对称轴的位置，对称轴在轴左边则，在轴的右侧则，概括的说就是“左同右异”
③常数项：总结起来，决定了抛物线与轴交点的位置．
【考点3 二次函数的图象与系数的关系】
【例3】（2022·辽宁朝阳·统考中考真题）如图，二次函数y＝ax2+bx+c（a为常数，且a≠0）的图象过点(﹣1，0)，对称轴为直线x＝1，且2＜c＜3，则下列结论正确的是（ ）
A．abc＞0B．3a+c＞0
C．a2m2+abm≤a2+ab（m为任意实数）D．﹣1＜a＜﹣
【变式3-1】（2022·内蒙古·中考真题）如图，抛物线（）的对称轴为直线，抛物线与x轴的一个交点坐标为），下列结论：①；②；③当时，x的取值范围是；④点，都在抛物线上，则有．其中结论正确的个数是（ ）
A．1个B．2个C．3个D．4个
【变式3-2】（2022·湖北荆门·统考中考真题）抛物线y＝ax2+bx+c（a，b，c为常数）的对称轴为x＝﹣2，过点（1，﹣2）和点（x0，y0），且c＞0．有下列结论：①a＜0；②对任意实数m都有：am2+bm≥4a﹣2b；③16a+c＞4b；④若＞﹣4，则＞c．其中正确结论的个数为( )
A．1个B．2个C．3个D．4个
【变式3-3】（2022·辽宁丹东·统考中考真题）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（5，0），与y轴交于点C，其对称轴为直线x＝2，结合图象分析如下结论：①abc＞0；②b+3a＜0；③当x＞0时，y随x的增大而增大；④若一次函数y＝kx+b（k≠0）的图象经过点A，则点E（k，b）在第四象限；⑤点M是抛物线的顶点，若CM⊥AM，则a＝．其中正确的有（ ）
A．1个B．2个C．3个D．4个
【考点4 二次函数的对称性】
【例4】（2022·四川自贡·统考中考真题）已知A(−3，−2) ，B(1，−2)，抛物线y=ax2+bx+c(a>0)顶点在线段AB上运动，形状保持不变，与x轴交于C，D两点（C在D的右侧），下列结论：
①c≥−2 ；
②当x>0时，一定有y随x的增大而增大；
③若点D横坐标的最小值为−5，点C横坐标的最大值为3；
④当四边形ABCD为平行四边形时，a=．
其中正确的是（ ）
A．①③B．②③C．①④D．①③④
【变式4-1】（2022·四川成都·统考中考真题）如图，二次函数的图像与轴相交于，两点，对称轴是直线，下列说法正确的是（ ）
A．B．当时，的值随值的增大而增大
C．点的坐标为D．
【变式4-2】（2022·北京昌平·统考二模）在平面直角坐标系中，已知抛物线．
(1)若抛物线过点．
①求抛物线的对称轴；
②当时，图像在轴的下方，当时，图像在轴的上方，在平面直角坐标系中画出符合条件的图像，求出这个抛物线的表达式；
(2)若，，为抛物线上的三点且，设抛物线的对称轴为直线，直接写出的取值范围．
【变式4-3】（2022·吉林长春·统考中考真题）在平面直角坐标系中，抛物线（b是常数）经过点．点A在抛物线上，且点A的横坐标为m（）．以点A为中心，构造正方形，，且轴．
(1)求该抛物线对应的函数表达式：
(2)若点B是抛物线上一点，且在抛物线对称轴左侧．过点B作x轴的平行线交抛物线于另一点C，连接．当时，求点B的坐标；
(3)若，当抛物线在正方形内部的点的纵坐标y随x的增大而增大时，或者y随x的增大而减小时，求m的取值范围；
(4)当抛物线与正方形的边只有2个交点，且交点的纵坐标之差为时，直接写出m的值．
【考点5 二次函数的最值】
【例5】（2022·浙江衢州·统考中考真题）已知二次函数，当时，的最小值为，则的值为（ ）
A．或4B．或C．或4D．或4
【变式5-1】（2022·浙江丽水·统考中考真题）如图，已知点在二次函数的图像上，且．
(1)若二次函数的图像经过点．
①求这个二次函数的表达式；
②若，求顶点到的距离；
(2)当时，二次函数的最大值与最小值的差为1，点M，N在对称轴的异侧，求a的取值范围．
【变式5-2】（2022·山东济南·济南育英中学校考模拟预测）在平面直角坐标系xOy中，已知抛物线与x轴交于A、B两点，与y轴交于C点，D为抛物线顶点．连接AD交y轴于点E，点P在第四象限的抛物线上，连接交于点G，设，则w的最小值是（ ）
A．B．C．D．
【变式5-3】（2022·天津滨海新·统考二模）已知：抛物线（b，c为常数），经过点A（－2，0），C（0，4），点B为抛物线与x轴的另一个交点．
(1)求抛物线的解析式；
(2)点P为直线BC上方抛物线上的一个动点，当△PBC的面积最大时，求点P的坐标；
(3)设点M，N是该抛物线对称轴上的两个动点，且，点M在点N下方，求四边形AMNC周长的最小值．
【考点6 待定系数法求二次函数的解析式】
【例6】（2022·内蒙古·中考真题）如图，抛物线经过，两点，与x轴的另一个交点为A，与y轴相交于点C．
(1)求抛物线的解析式和点C的坐标；
(2)若点M在直线上方的抛物线上运动（与点B，C不重合），求使面积最大时M点的坐标，并求最大面积；（请在图1中探索）
(3)设点Q在y轴上，点P在抛物线上，要使以点A，B，P，Q为顶点的四边形是平行四边形，求所有满足条件的点P的坐标．（请在图2中探索）
【变式6-1】（2022·四川巴中·统考中考真题）如图1，抛物线，交轴于A、B两点，交轴于点，为抛物线顶点，直线垂直于轴于点，当时，．
(1)求抛物线的表达式；
(2)点是线段上的动点（除、外），过点作轴的垂线交抛物线于点．
①当点的横坐标为2时，求四边形的面积；
②如图2，直线，分别与抛物线对称轴交于、两点．试问，是否为定值？如果是，请求出这个定值；如果不是，请说明理由．
【变式6-2】（2022·辽宁鞍山·统考中考真题）如图，抛物线与轴交于，两点，与轴交于点，连接．
(1)求抛物线的解析式．
(2)点是第三象限抛物线上一点，直线与轴交于点，的面积为12，求点的坐标．
(3)在（2）的条件下，若点是线段上点，连接，将沿直线翻折得到，当直线与直线相交所成锐角为时，求点的坐标．
【变式6-3】（2022·江苏镇江·统考中考真题）一次函数的图像与轴交于点，二次函数的图像经过点、原点和一次函数图像上的点．
(1)求这个二次函数的表达式；
(2)如图1，一次函数与二次函数的图像交于点、（），过点作直线轴于点，过点作直线轴，过点作于点．
①_________，_________（分别用含的代数式表示）；
②证明：；
(3)如图2，二次函数的图像是由二次函数的图像平移后得到的，且与一次函数的图像交于点、（点在点的左侧），过点作直线轴，过点作直线轴，设平移后点、的对应点分别为、，过点作于点，过点作于点．
①与相等吗？请说明你的理由；
②若，求的值．
【要点4 二次函数图象的平移变换】
（1）平移步骤：
①将抛物线解析式转化成顶点式，确定其顶点坐标；
②保持抛物线的形状不变，将其顶点平移到处，具体平移方法如下：
（2）平移规律：在原有函数的基础上“值正右移，负左移；值正上移，负下移”．概括成八个字“左加右减，上加下减”．
【考点7 二次函数图象的平移】
【例7】（2022·四川巴中·统考中考真题）函数的图象是由函数的图象轴上方部分不变，下方部分沿轴向上翻折而成，如图所示，则下列结论正确的是（ ）
① ；②； ③；④将图象向上平移1个单位后与直线有3个交点．
A．①②B．①③C．②③④D．①③④
【变式7-1】（2022·上海·统考中考真题）已知：经过点，．
(1)求函数解析式；
(2)平移抛物线使得新顶点为（m＞0）．
①倘若，且在的右侧，两抛物线都上升，求的取值范围；
②在原抛物线上，新抛物线与轴交于，时，求点坐标．
【变式7-2】（2022·浙江嘉兴·统考中考真题）已知抛物线L1：y＝a(x＋1)2－4（a≠0）经过点A(1，0)．
(1)求抛物线L1的函数表达式．
(2)将抛物线L1向上平移m（m＞0）个单位得到抛物线L2．若抛物线L2的顶点关于坐标原点O的对称点在抛物线L1上，求m的值．
(3)把抛物线L1向右平移n（n＞0）个单位得到抛物线L3，若点B(1，y1)，C(3，y2)在抛物线L3上，且y1＞y2，求n的取值范围．
【变式7-3】（2022·湖南岳阳·统考中考真题）如图1，在平面直角坐标系中，抛物线：经过点和点．
(1)求抛物线的解析式；
(2)如图2，作抛物线，使它与抛物线关于原点成中心对称，请直接写出抛物线的解析式；
(3)如图3，将（2）中抛物线向上平移2个单位，得到抛物线，抛物线与抛物线相交于，两点（点在点的左侧）．
①求点和点的坐标；
②若点，分别为抛物线和抛物线上，之间的动点（点，与点，不重合），试求四边形面积的最大值．
【要点5 二次函数与一元二次方程之间的关系】
【考点8 二次函数与一元二次方程】
【例8】（2022·湖北恩施·统考中考真题）已知抛物线，当时，；当时，．下列判断：
①；②若，则；③已知点，在抛物线上，当时，；④若方程的两实数根为，，则．
其中正确的有（ ）个．
A．1B．2C．3D．4
【变式8-1】（2022·山西·中考真题）阅读与思考
下面是小宇同学的数学小论文，请仔细阅读并完成相应的任务
任务：
(1)上面小论文中的分析过程，主要运用的数学思想是 （从下面选项中选出两个即可）；
A．数形结合
B．统计思想
C．分类讨论．
D．转化思想
(2)请参照小论文中当时①②的分析过程，写出③中当时，一元二次方程根的情况的分析过程，并画出相应的示意图；
(3)实际上，除一元二次方程外，初中数学还有一些知识也可以用函数观点来认识，例如：可用函数观点来认识一元一次方程的解．请你再举出一例为
【变式8-2】（2022·四川自贡·统考中考真题）已知二次函数．
(1)若，且函数图象经过，两点，求此二次函数的解析式，直接写出抛物线与轴交点及顶点的坐标；
(2)在图①中画出（1）中函数的大致图象，并根据图象写出函数值时自变量的取值范围；
(3)若且，一元二次方程 两根之差等于，函数图象经过，两点，试比较的大小 ．
【变式8-3】（2023·福建泉州·泉州五中校考三模）已知抛物线，a、b、c为实数．
(1)当且时
①若抛物线的对称轴为直线，求抛物线的解析式；
②若中，恒有，求c的取值范围；
(2)若抛物线与x轴只有一个公共点，与y轴交于；直线与抛物线交于点P、Q，过点P且与y轴平行的直线与直线MQ相交于点N，求证：对于每个给定的实数k，点N的纵坐标均为定值．
【考点9 利用二次函数的图象确定一元二次方程的近似根】
【例9】（2022·山东聊城·统考三模）观察下列表格，估计一元二次方程的正数解在（ ）
A．－1和0之间B．0和1之间C．1和2之间D．2和3之间
【变式9-1】（2022·浙江金华·统考一模）方程的根可视为函数的图象与函数的图象交点的横坐标，那么用此方法可推断出方程的实数根x所在的范围是（ ）
A．B．
C．D．
【变式9-2】（2022·河南洛阳·统考一模）为解方程，小舟根据学习函数的经验对其进行了探究，下面是其探究的过程，请补充完整：
(1)先研究函数，列表如下：
表格中，m的值为______．
(2)如图，在平面直角坐标系中，描出了以上表中各组对应值为坐标的点，根据描出的点，画出了函数图象的一部分，请根据剩余的点补全此函数图象．
(3)观察图象，当时，满足条件的x的取值范围是______．
(4)在第（2）间的平面直角坐标系中画出直线．根据图象直接写出方程的近似解（结果保留一位小数）．
【变式9-3】（2022·江苏宿迁·统考一模）我们知道，可以借助于函数图象求方程的近似解．如图（甲），把方程x﹣2＝1﹣x的解看成函数y＝x﹣2的图象与函数y＝1﹣x的图象的交点的横坐标，求得方程x﹣2＝1﹣x的解为x＝1.5．
(1)如图（乙），已画出了反比例函数在第一象限内的图象，借助于此图象求出方程2x2﹣2x﹣1＝0的正数解．（要求画出相应函数的图象，结果精确到0.1）
(2)选择：三次方程x3﹣x2﹣2x+1＝0的根的正负情况是 ．
A，有两个负根，一个正根
B．有三个负根
C．有一个负根，两个正根
D．有三个正根
【考点10 二次函数与不等式】
【例10】（2022·浙江宁波·一模）已知A，B两点的坐标分别为，，线段上有一动点，过点M作x轴的平行线交抛物线于两点（P在Q的左侧）．若恒成立，则a的取值范围为（ ）
A．B．C．D．
【变式10-1】（2022·新疆乌鲁木齐·校考三模）如图，抛物线与直线交于A、B两点，下列是关于x的不等式或方程，结论正确的是（ ）
A．的解集是
B．的解集是
C．的解集是
D．的解是或
【变式10-2】（2022·新疆乌鲁木齐·乌鲁木齐市第九中学校考三模）如图，在平面直角坐标系中，抛物线与直线（m、b均为常数）交于点和点B．
(1)求m和b的值；
(2)求点B的坐标，并结合图象写出不等式的解集；
(3)点M是直线AB上的一个动点，点N在点M正下方（即轴），且，若线段MN与抛物线只有一个公共点，请直接写出点M的横坐标的取值范围．
【变式10-3】（2022·河南洛阳·统考一模）如图，抛物线的图象与x轴交点为A和B，与y轴交点为，与直线交点为A和C．
(1)求抛物线的解析式；
(2)求点C的坐标，并结合函数图象直接写出当时x的取值范围；
(3)若点E是x轴上一个动点，把点E向下平移4个单位长度得到点F，点F向右平移4个单位长度得到点G，点G向上平移4个单位长度得到点H，若四边形与抛物线有公共点，请直接写出点E的横坐标的取值范围． y=ax2
y=ax2+k
y=a(x-h)2
y=a(x-h)2+k
y=ax2+bx+c
对称轴
y轴
y轴
x=h
x=h
顶点
(0，0)
(0，k)
(h，0)
(h，k)
a>0时，顶点是最低点，此时y有最小值；a0
x0(h或)时，y随x的增大而增大。
即在对称轴的左边，y随x的增大而减小；在对称轴的右边，y随x的增大而增大。
a