人教版（2024）九年级上册24.1.1 圆课时训练

这是一份人教版（2024）九年级上册24.1.1 圆课时训练，共16页。
TOC \ "1-4" \h \z \u \l "_Tc28033" PAGEREF _Tc28033 \h 1
\l "_Tc4100" 模型1.定点定长共圆模型（圆的定义） PAGEREF _Tc4100 \h 2
\l "_Tc15317" 模型2.定边对双直角共圆模型 PAGEREF _Tc15317 \h 6
\l "_Tc20167" 模型3.定边对定角共圆模型 PAGEREF _Tc20167 \h 11
\l "_Tc8564" 模型4.对角互补共圆模型 PAGEREF _Tc8564 \h 14
\l "_Tc23247" 19
【知识储备】
四点共圆：若在同一平面内，有四个点在同一个圆上，则称这四个点共圆，一般简称为“四点共圆”。
四点共圆模型是一种解题思想，但任何题目里都不会告诉你，亲爱的同学，请用四点共圆思想来解题吧。那么，我们头脑里，就要快速迭代平常积累的一些模型。
四点共圆有三个性质：（1）共圆的四个点所连成同侧共底的两个三角形的顶角相等；（2）圆内接四边形的对角互补；（3）圆内接四边形的外角等于内对角。
模型1.定点定长共圆模型（圆的定义）
若四个点到一定点的距离相等，则这四个点共圆。这也是圆的基本定义，到定点的距离等于定长点的集合。
条件：如图，平面内有五个点O、A、B、C、D，使得OA=OB=OC=OD。
结论：A、B、C、D四点共圆（其中圆心为O）。
证明：∵OA=OB=OC=OD
∴根据圆的定义：到定点的距离等于定长点的集合为圆，确定A、B、C、D四点共圆。
例1．（2021·浙江嘉兴·中考真题）如图，在中，，AB=AC=5，点在上，且，点E是AB上的动点，连结，点，G分别是BC，DE的中点，连接，，当AG=FG时，线段长为（ ）
A．B．C．D．4
变式1．（2023·江西赣州·九年级校联考期中）如图，点O为线段AB的中点，点B，C，D到点O的距离相等，连接AC，BD．则下面结论不一定成立的是（ ）
A．∠ACB=90° B．∠BDC=∠BAC C．AC平分∠BAD D．∠BCD+∠BAD=180°
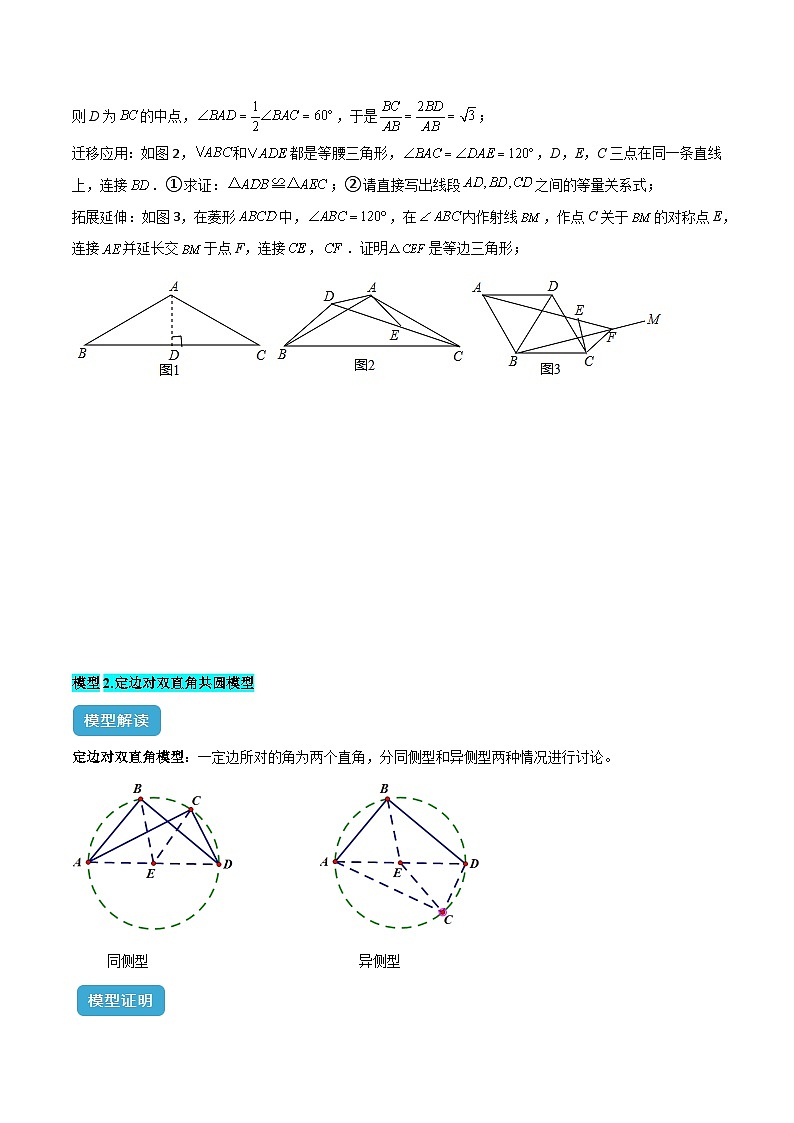
变式2．（2023·湖北·三模）问题背景：如图1，等腰中，，作于点D，则D为的中点，，于是；
迁移应用：如图2，和都是等腰三角形，，D，E，C三点在同一条直线上，连接．①求证：；②请直接写出线段之间的等量关系式；
拓展延伸：如图3，在菱形中，，在内作射线，作点C关于的对称点E，连接并延长交于点F，连接，．证明是等边三角形；
模型2.定边对双直角共圆模型
定边对双直角模型：一定边所对的角为两个直角，分同侧型和异侧型两种情况进行讨论。

同侧型 异侧型
1）定边对双直角模型（同侧型）
条件：若平面上A、B、C、D四个点满足，
结论：A、B、C、D四点共圆，其中AD为直径。
2）定边对双直角模型（异侧型）
条件：若平面上A、B、C、D四个点满足，
结论：A、B、C、D四点共圆，其中AD为直径。
注意：由于同侧型与异侧型证明相同，故下面证明一次即可。
证明：取AD的中点为E，连结BE，CE。 ∵，BE=CE=AD=AE=ED，
∴根据圆的定义：到定点的距离等于定长点的集合为圆，确定A、B、C、D四点共圆。
例1．（2024·陕西西安·模拟预测）如图，线段，以为斜边构造等腰直角和直角，、在两侧，平分交于点，则的最小值为 ．
例2．（2023·山东烟台·九年级统考期中）如图，平面直角坐标系中，点A、B坐标分别为（3，0）、（0，4），点C是x轴正半轴上一点，连接BC．过点A垂直于AB的直线与过点C垂直于BC的直线交于点D，连接BD，则的值是 ．
变式1．（2023·贵州·统考中考真题）如图①，小红在学习了三角形相关知识后，对等腰直角三角形进行了探究，在等腰直角三角形中，，过点作射线，垂足为，点在上．

(1)【动手操作】如图②，若点在线段上，画出射线，并将射线绕点逆时针旋转与交于点，根据题意在图中画出图形，图中的度数为_______度；
(2)【问题探究】根据（1）所画图形，探究线段与的数量关系，并说明理由；
(3)【拓展延伸】如图③，若点在射线上移动，将射线绕点逆时针旋转与交于点，探究线段之间的数量关系，并说明理由．
变式2．（2023·广东梅州·九年级校考阶段练习）如图，在四边形 中，， 是 的中点， 是 的中点，若 ，，，则 的长为（ ）

A．B．C．D．
模型3.定边对定角共圆模型
定边对定角模型：一定边同侧所对的角为两个相等（为定值）。

图1 图2
条件：如图1，平面上A、B、C、D四个点满足，结论：A、B、C、D四点共圆。
条件：如图2，AC、BD交于H，，结论：四点共圆。
证明：∵，∴，
又∵，。∴，
∴A、B、C、D四点共圆。
例1．（23-24九年级·福建福州·期中）如图，在RtABC中，∠BAC＝90°，∠ABC＝40°，将ABC绕A点顺时针旋转得到ADE，使D点落在BC边上．（1）求∠BAD的度数；（2）求证：A、D、B、E四点共圆．
变式1．（23-24九年级上·陕西西安·阶段练习）如图，在四边形中，，对角线平分，，且．(1)证明：；(2)若，，求的长．

变式2．（2022·江苏无锡·中考真题）△ABC是边长为5的等边三角形，△DCE是边长为3的等边三角形，直线BD与直线AE交于点F．如图，若点D在△ABC内，∠DBC=20°，则∠BAF＝________°；现将△DCE绕点C旋转1周，在这个旋转过程中，线段AF长度的最小值是________．
模型4.对角互补共圆模型

图1 图2
条件：如图1，平面上A、B、C、D四个点满足，结论：A、B、C、D四点共圆．
条件：如图2，BA、CD的延长线交于P，， 结论：A、B、C、D四点共圆.
证明：∵，∴，
又∵，。∴，∵，∴
∴A、B、C、D四点共圆。
例1．（23-24九年级上·云南昆明·期中）综合与实践：“善思”小组开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆．该小组继续利用上述结论进行探究．
提出问题：如图1所示，在线段同侧有两点，，连接，，，，如果，那么，，，四点在同一个圆上．

探究展示：如图2所示，作经过点，，的，在劣弧上取一点（不与，重合），
连接，，则，（依据
，，
点，，，四点在同一个圆上，（对角互补的四边形四个顶点共圆）
点，在点，，所确定的上，（依据
点，，，四点在同一个圆上；
反思归纳：（1）上述探究过程中的“依据1”、“依据2”分别是指什么？
依据1：______；（从右边框内选一个选项，直接填序号）
依据2：______．（从右边框内选一个选项，直接填序号）
（2）如图3所示，在四边形中，，，则的度数为______．
变式1．（2023·河南周口·校考三模）在中，，M是外一动点，满足，若，，，则的长度为 ．

变式2．（2023·江苏·九年级假期作业）如图，，，点、分别是线段、射线上的动点，以为斜边向上作等腰，，连接，则的最小值为 ．
1．（2023·浙江·统考中考真题）如图，在四边形中，，以为腰作等腰直角三角形，顶点恰好落在边上，若，则的长是（ ）

A．B．C．2D．1
2．（2023·广西·中考模拟）如图所示，四边形ABCD中，DC∥AB，BC=1，AB=AC=AD=2．则BD的长为（ ）
A． B． C． D．
3．（2024·湖北武汉·模拟预测）如图，是的直径，点E在上，垂足为C，点G在上运动（不与E重合），点F为的中点，则的最大值为（ ）
A．B．6C．D．8
4．（23-24九年级上·江苏苏州·阶段练习）如图，点A，B在上，P为外一点，且，，连接OP，OP与相交于点C，与AB交于点D，连接，，有下列结论：①；②；③C为中点；④四边形为菱形；⑤O，A，B，P四点共圆，其中一定成立的有（ ）个
A．2B．3C．4D．5
5．（23-24九年级上·黑龙江绥化·期中）如图放置的两个正方形，大正方形的边长为，小正方形的边长为，点在边上，且，连接，，交于点，将绕点旋转至，将绕点旋转至，下列结论：
①；②；③；④，，，四点共圆．其中结论正确的序号是（ ）
A．①②③B．②③④C．①②③④D．①④
6．（2023·江苏无锡·统考一模）如图，是的直径，点C在上，，垂足为D，，点E是上的动点（不与C重合），点F为的中点，若在E运动过程中的最大值为4，则的值为（ ）
A．B．C．D．
7．（2023·安徽合肥·校联考二模）动点在等边的边上，，连接，于，以为一边作等边，的延长线交于，当取最大值时，的长为（ ）
A．B．C．D．
8．（2023·河北·唐山九年级阶段练习）如图所示，在四边形ABCD中，AB=AC=AD，∠BAC=26°，∠CAD=74°，则∠BCD=_______°，∠DBC_______°．
9．（2024·陕西西安·三模）如图，正方形的边长为8，M、N为边上的动点，以为斜边作等腰（其中），点E在边上，且，连接，则的周长最小值为 ．

10．（2023·重庆·九年级统考期中）如图，在中，，点是边的中点，连结，将沿直线翻折得到，连结．若，则线段的长为 ．
11．（2024·浙江杭州·九年级月考）如图，已知，的内切圆分别切边于点直线分别与直线相交于点.求证：．
12．（2023·江苏·九年级假期作业）如图，，是的高，，相交于点，是的中点，是的外接圆．(1)点B，C，D，E是否在以点M为圆心的同一个圆上？请说明理由．
(2)若，，求外接圆的半径长．

13．（2023上·江苏宿迁·九年级校考阶段练习）（1）【基础巩固】如图1，内接于，若，弦，则半径______；
（2）【问题探究】如图2，四边形的四个顶点均在上，若，，点为弧上一动点（不与点，点重合）．
求证：；
（3）【解决问题】如图3，一块空地由三条直路（线段、、）和一条道路劣弧CD围成，已知千米，，CD的半径为1千米，市政府准备将这块空地规划为一个公园，主入口在点M处，另外三个入口分别在点C、D、P处，其中点在CD上，并在公园中修四条慢跑道，即图中的线段、、、，某数学兴趣小组探究后发现C、P、D、M四个点在同一个圆上，请你帮他们证明C、P、D、M四点共圆，并判断是否存在一种规划方案，使得四条慢跑道总长度（即四边形的周长）最大？若存在，求其最大值；若不存在，说明理由．

14．（2023·绵阳市·九年级专题练习）如图所示中，，，分别在边和上，且，，垂足分别为，，求的长.
15．（2022春·山东·九年级专题练习）定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．
（1）如图1，∠E是△ABC中∠A的遥望角．①若∠A＝40°，直接写出∠E的度数是 ；
②求∠E与∠A的数量关系，并说明理由．（2）如图2，四边形ABCD中，∠ABC＝∠ADC＝90°，点E在BD的延长线上，连CE，若∠BEC是△ABC中∠BAC的遥望角，求证：DA＝DE．
16．（2023·广东九年级统考期末）如图，在中，，点为线段一点，连接，将绕点旋转至，连接和（）．

(1)如图1，若，，点P是延长线一点，连接，若，，，求的长；(2)如图2，，作于点交于点，求证：；
(3)如图3，在（2）的条件下，若，点是直线上一动点，连接，当点运动到中点时，将沿翻折至，连接，请直接写出面积的最大值．
17．（2023·江苏盐城·九年级校考阶段练习）在边长为12cm的正方形ABCD中，点E从点D出发，沿边DC以1cm/s的速度向点C运动，同时，点F从点C出发，沿边CB以1cm/s的速度向点B运动，当点E达到点C时，两点同时停止运动，连接AE、DF交于点P，设点E． F运动时间为t秒．回答下列问题：
(1)如图1，当t为多少时，EF的长等于cm?(2)如图2，在点E、F运动过程中，①求证：点A、B、F、P在同一个圆(⊙O)上；②是否存在这样的t值，使得问题①中的⊙O与正方形ABCD的一边相切?若存在，求出t值；若不存在，请说明理由；③请直接写出问题①中，圆心O的运动的路径长为_________．
18．（2023·绵阳市九年级课时练习）如图，四边形内接于，对角线，垂足为，于点，直线与直线于点．
（1）若点在内，如图1，求证：和关于直线对称；
（2）连接，若，且与相切，如图2，求的度数．①圆内接四边形对角互补；
②对角互补的四边形四个顶点共圆；
③过不在同一直线上的三个点有且只有一个圆；
④经过两点的圆的圆心在这两点所连线段的垂直平分线上；