人教版（2024）九年级上册24.3 正多边形和圆评优课ppt课件

这是一份人教版（2024）九年级上册24.3 正多边形和圆评优课ppt课件，共21页。PPT课件主要包含了学习目标，导入新课，正多边形，各边相等，各角相等，缺一不可，讲授新课，探究归纳，想一想，完成下面的表格等内容，欢迎下载使用。
1. 了解正多边形和圆的有关概念；2. 理解并掌握正多边形的半径、中心角、边心距、边 长之间的关系；（重点）3. 会应用正多边形和圆的有关知识解决实际问题.（难点）
24.3 正多边形和圆
下图的这些图案，都是我们在日常生活中经常看到的.你能从这些图案中找出类似的图形吗?
问题1 什么叫做正多边形？
各边相等，各角也相等的多边形叫做正多边形.
问题2 矩形是正多边形吗？为什么？ 菱形是正多边形吗？为什么？
矩形不是正多边形，因为矩形不符合各边相等；
菱形不是正多边形，因为菱形不符合各角相等.
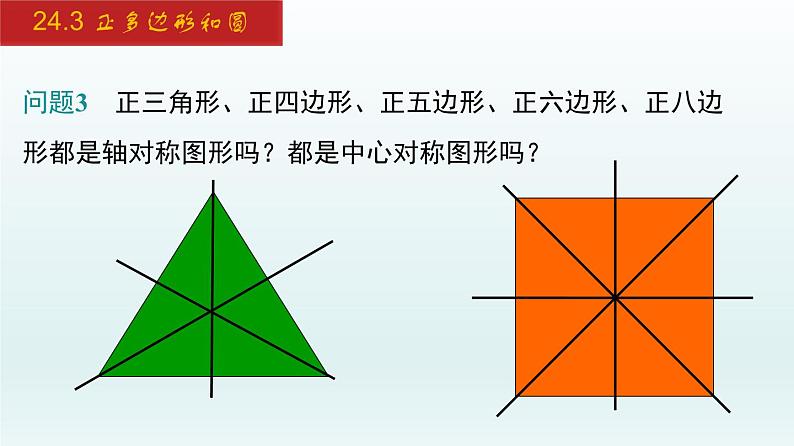
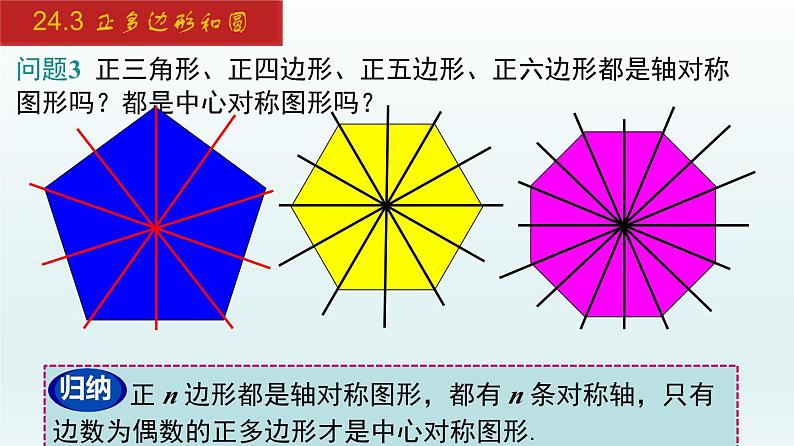
问题3 正三角形、正四边形、正五边形、正六边形、正八边形都是轴对称图形吗？都是中心对称图形吗？
正 n 边形都是轴对称图形，都有 n 条对称轴，只有边数为偶数的正多边形才是中心对称图形.
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗？都是中心对称图形吗？
问题1 怎样把一个圆进行四等分？
问题2 依次连接各等分点，得到一个什么图形？
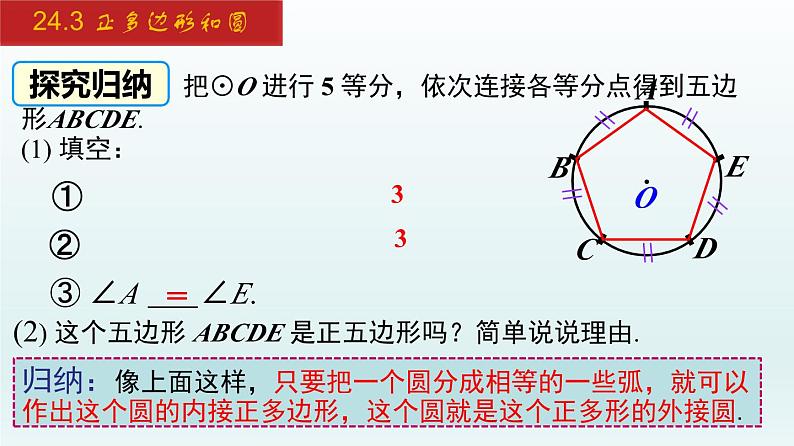
把⊙O 进行 5 等分，依次连接各等分点得到五边形ABCDE.(1) 填空：
(2) 这个五边形 ABCDE 是正五边形吗？简单说说理由.
归纳：像上面这样，只要把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形，这个圆就是这个正多形的外接圆.
问题3 以正方形为例，根据对称性，你能得出什么结论？
结论一：正方形 ABCD 有一个以点 O 为圆心的外接圆.证明：∵ EF 是边 AB、CD 的垂直平分线，∴ OA = OB，OD = OC.∵ GH 是边 AD、BC 的垂直平分线，∴ OA = OD，OB = OC.∴ OA = OB = OC = OD.
∴ 正方形 ABCD 有一个以点 O 为圆心的外接圆.
证明：∵ AC、CA 分别是∠DAB 及∠DCB 的平分线，BD、DB 分别是∠ABC 及∠ADC 的平分线，
∴ OE = OH = OF = OG.
∴ 正方形 ABCD 有一个以点 O 为圆心的内切圆.
结论二：正方形 ABCD 有一个以点 O 为圆心的内切圆.
所有的正多边形是不是都有一个外接圆和一个内切圆？
任何正多边形都有一个外接圆和一个内切圆，且圆心相同.
正多边形的外接圆和内切圆的公共圆心，叫做正多边形的中心
外接圆的半径叫做正多边形的半径
内切圆的半径叫做正多边形的边心距
正多边形的外角 = 中心角
如图，已知半径为 4 的圆内接正六边形 ABCDEF：① 它的中心角等于 度；② OC BC(填＞、＜或＝）；③ △OBC 是 三角形； ④ 圆内接正六边形的面积是 △OBC 面积 的 倍.⑤ 圆内接正 n 边形面积公式：___________________.
例1 如图，正五边形 ABCDE 内接于⊙O，则∠ADE 的 度数是 （ ） A．60° B．45° C．36° D．30°
解析：由五边形 ABCDE 是正五边形且内接于⊙O，可求出弧 AE 所对的圆心角的度数等于 360°÷5 = 72°，再根据圆周角定理可得到∠ADE 的度数.
变式题 如图，圆内接正五边形 ABCDE 中，对角线 AD 和 CE 相交于点 P，则∠APE 的度数是（　　）A．36° B．60°C．72° D．108°
解析：由例 1 易得∠ADE = ∠CED = 36°，根据三角形的外角性质，得∠APE = ∠ADE + ∠CED = 72°.
例2 有一个亭子，它的地基是半径为 4 m 的正六边形，求地基的周长和面积 (面积保留小数点后一位 ).
解：连接 OB，过点 O 作 OM⊥BC 于 M.
亭子地基的周长 l = 6×4 = 24 (m)，
2.作边心距，构造直角三角形.
1.连半径，得中心角；
圆内接正多边形的辅助线