

数学九年级上册24.3 正多边形和圆课文ppt课件
展开1.理解并掌握正多边形的半径和边长、边心距、中心角之间的关系. (重点)2.会进行特殊的与正多边形有关的计算,会画某些正多边形. (难点)
1.对角互补;2.四个内角的和是360°;3.任一外角与其相邻的内角的对角相等(即外角等于内对角).
下面这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗?
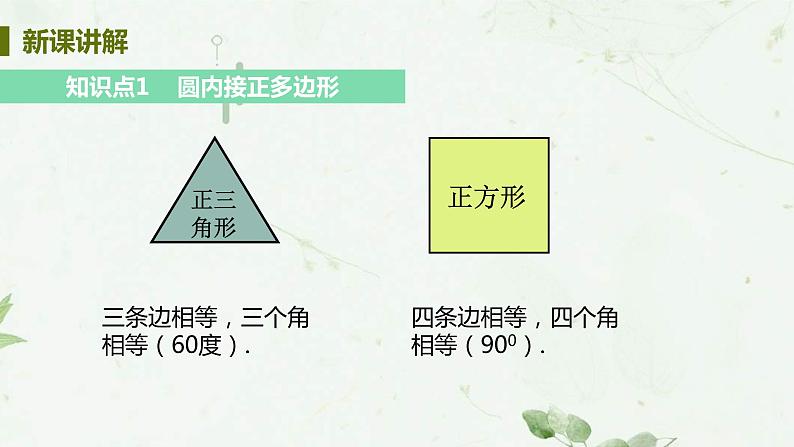
知识点1 圆内接正多边形
三条边相等,三个角相等(60度).
四条边相等,四个角相等(900).
各边相等、各角也相等的多边形叫做正多边形.
矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
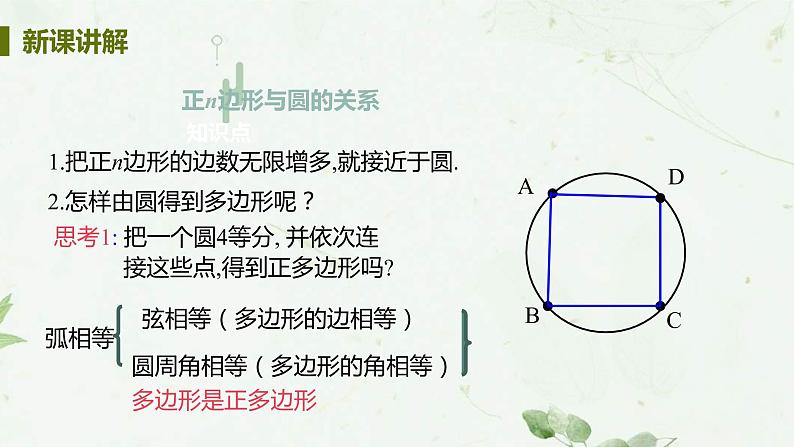
1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢?
思考1: 把一个圆4等分, 并依次连 接这些点,得到正多边形吗?
弦相等(多边形的边相等)
圆周角相等(多边形的角相等)
下列说法中,不正确的是( ) A.正多边形一定有一个外接圆和一个内切圆 B.各边相等且各角相等的多边形是正多边形 C.正多边形的内切圆和外接圆是同心圆 D.正多边形既是轴对称图形,又是中心对称图形
知识点2 圆内接正多边形的有关概念
正多边形的中心: 一个正多边形的外接圆的圆心.
正多边形的半径: 外接圆的半径
正多边形的中心角: 正多边形的每一条边所对的圆心角.
正多边形的边心距: 中心到正多边形的一边的距离.
1 正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.请以圆内接正五边形为例进行证明.
证明:如图,把⊙O分成相等的5段弧,依次连接各分点得到五边形ABCDE. ∵AB=BC=CD=DE=EA, ∴AB=BC=CD=DE=EA, BCE=3AB=CDA. ∴∠A=∠B. 同理∠B=∠C=∠D=∠E. 又五边形ABCDE的顶点都在⊙O上, ∴五边形ABCDE是⊙O的内接正五边形, ⊙O是正五边形ABCDE的外接圆.
2 如图,有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积(结果保留小数点后一位).
解:如图,连接OB,OC.因为六边形ABCDEF是正六边形,所 以它的中心角等于 =60°,△OBC是等边三角形,从而 正六边形的边长等于它的半径. 因此,亭子地基的周长l=6×4=24(m). 作OP⊥BC,垂足为P. 在Rt△OPC中,OC=4 m, PC= =2(m),利用勾股定理, 可得边心距r= 亭子地基的面积S=
正n边形的一个内角的度数是多少?中心角呢?正多边形的中心角与外角的大小有什么关系?
一元钱硬币的直径约为24 mm,则用它能完全覆盖住的正六边形的边长最大不能超过( )A.12 mm B.12 mmC.6 mm D.6 mm
知识点3 正多边形的作图
正多边形和圆有什么关系?你能借助圆画一个正多边形吗?
已知⊙O 的半径为 2 cm,画圆的内接正三角形.
度量法①:用量角器或 30°角的三角板度量,使∠BAO=∠CAO=30°.
度量法②:用量角器度量,∠AOB=∠BOC=∠COA=120°.
度量法③:用圆规在⊙O 上顺次截取6条长度等于半径(2 cm)的弦,连接其中的 AB,BC,CA 即可.
用量角器等分圆: 由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可以等分圆周,从而得到正多边形.采用“先用量角器画一个 的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”.这种方法简便,且可以画任意正多边形、误差小.
用尺规等分圆: 用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形,这种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上讲是一种准确方法,但在作图时较复杂,同样存在作图的误差.
添加辅助线的方法:连半径,作边心距
此方法可将圆任意n等分,所以用该方法可作出任意正多边形,但边数很大时,容易产生较大的误差.
此方法是一种比较准确的等分圆的方法,但有局限性,不能将圆任意等分.
1.下列说法中正确的是( )A.各边都相等的多边形是正多边形B.正多边形既是轴对称图形,又是中心对称图形C.各边都相等的圆内接多边形是正多边形D.各角都相等的圆内接多边形是正多边形
2.如果一个正多边形的每个外角都等于36°,则这个多边形的中心角等于( )A.36° B.18° C.72° D.54°3.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使直角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )A.4 B.5 C.6 D.7
初中数学24.3 正多边形和圆图文ppt课件: 这是一份初中数学24.3 正多边形和圆图文ppt课件,共26页。
初中数学人教版九年级上册24.3 正多边形和圆示范课ppt课件: 这是一份初中数学人教版九年级上册24.3 正多边形和圆示范课ppt课件,共19页。PPT课件主要包含了学习目标,导入新知,合作探究,典型例题,课堂练习,中考实题,用量角器等分圆,正多边形的画法,用尺规等分圆,归纳新知等内容,欢迎下载使用。
人教版九年级上册第二十四章 圆24.3 正多边形和圆备课ppt课件: 这是一份人教版九年级上册第二十四章 圆24.3 正多边形和圆备课ppt课件,共12页。PPT课件主要包含了复习并导入,例题学习,变式题,能力提升,说一说自己的收获,P8978等内容,欢迎下载使用。