浙教版（2024）八年级下册第五章 特殊平行四边形5.3 正方形教案配套ppt课件

掌握正方形的判定方法，利用判定方法解决实际问题.
综合运用平行四边形、菱形、矩形、正方形的定理并探究中点四边形的问题.
理解特殊的平行四边形之间的内在联系，培养学生辩证看问题的观点.
体会探索和证明过程中所蕴含的抽象、归纳、推理等数学思想.
有一个角是直角且一组邻边相等的平行四边形叫做正方形
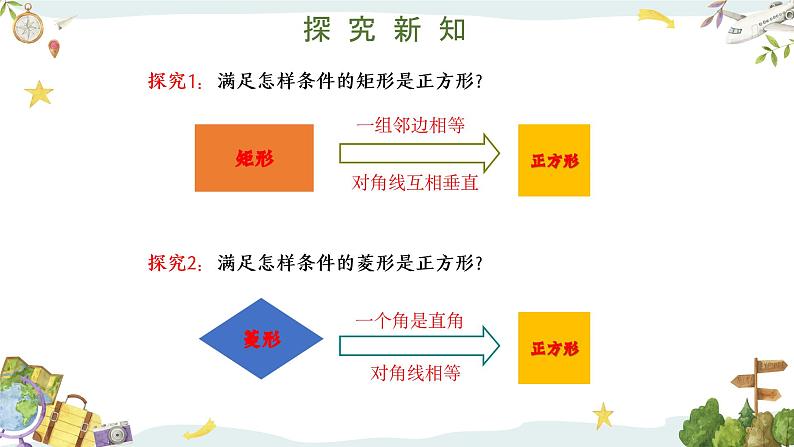
探究1：满足怎样条件的矩形是正方形？
探究2：满足怎样条件的菱形是正方形？
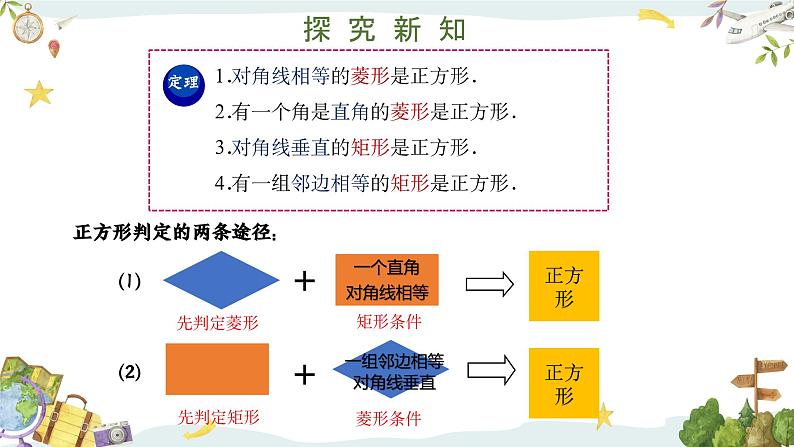
1.对角线相等的菱形是正方形.2.有一个角是直角的菱形是正方形.3.对角线垂直的矩形是正方形.4.有一组邻边相等的矩形是正方形.
正方形判定的两条途径：
例1：如图，在△ABC中，∠ACB=90°，CD为角平分线，DE⊥AC于点E，DF⊥BC于点F．求证：四边形CEDF是正方形．
证明 ∵DE⊥AC,DF⊥BC, ∠ACB=90°
∴ DE=DF , ∠DEC=∠DFC=90° ，∴四边形CEDF是矩形. ∵ CD为角平分线,∴DE=DF.∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).
例2：如图，在菱形ABCD中，对角线AC,BD相交于点O，点E,F在对角线BD上，且BE=DF,OA=OE．求证：四边形AECF是正方形．
解 ∵ 四边形ABCD是菱形，
∴ AC⊥BD，OA=OC，OB=OD.
∴ □ AECF是菱形.
∵ OE=OF=OA=OC，
∴ 菱形AECF是正方形.
做一做：顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形各边中点能得到怎样的特殊平行四边形？
有一个角是90°（或对角线互相垂直）
有一对邻边相等（或对角线相等）
一组邻边相等且一个内角为直角（或对角线互相垂直平分且相等）
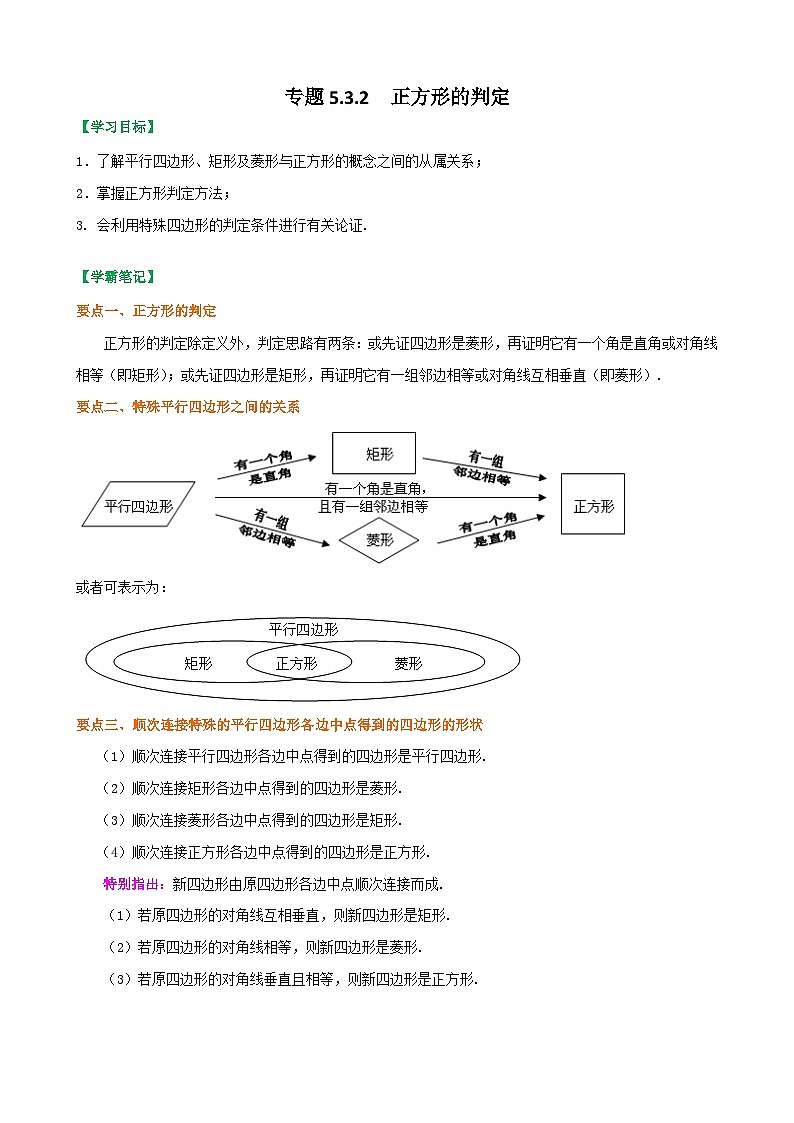
①定义：有一外角是直角的平行四边形 ②三个角是直角的四边形③对角线相等的平行四边形
①定义：一组邻边相等的平行四边形 ②四条边都相等的四边形③对角线互相垂直的平行四边形
①定义：一组邻边相等且有一个角是直角的平行四边形②有一组邻边相等的矩形 ③有一个角是直角的菱形