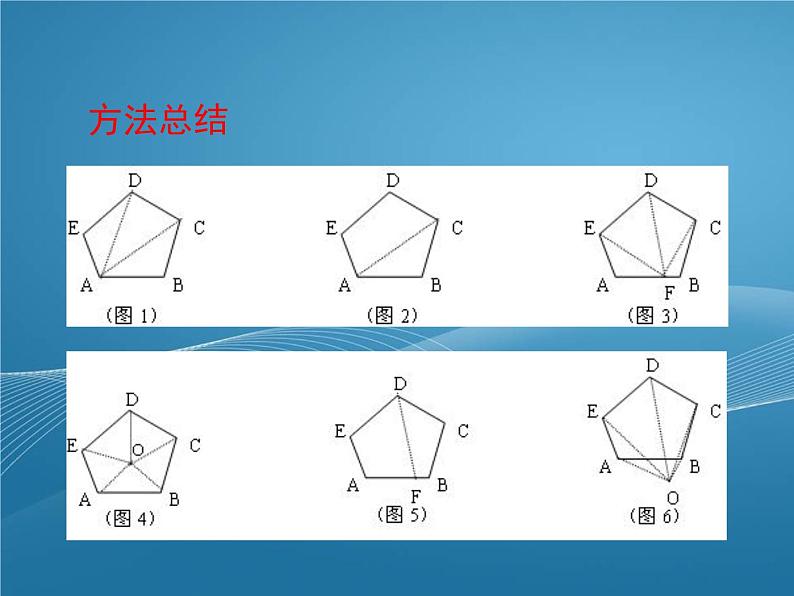
鲁教版（五四学制）（2024）八年级上册4 多边形的内角与外角和多媒体教学ppt课件

这是一份鲁教版（五四学制）（2024）八年级上册4 多边形的内角与外角和多媒体教学ppt课件，共16页。PPT课件主要包含了方法总结，×180°，n-3，n-2，归纳总结，思维升华等内容，欢迎下载使用。
教学目标【知识与技能】掌握多边形内角和定理，进一步了解转化的数学思想【过程与方法】经历质疑、猜想、归纳等活动，发展学生的合情推理能力，积累数学活动的经验，在探索中学会与人合作，学会交流自己的思想和方法．【情感态度与价值观】让学生体验猜想得到证实的成功喜悦和成就感，在解题中感受生活中数学的存在，体验数学充满着探索和创造．教学重难点【教学重点】多边形内角和定理的探索和应用【教学难点】多边形定义的理解；多边形内角和公式的推导；转化的数学思维方法的渗透．
1．三角形是如何定义的？2．仿照三角形定义，你能学着给四边形、五边形……n边形下定义吗？
1．三角形的内角和是多少度？你是怎么得出的？
2．四边形的内角和是多少？你又是怎样得出的？
① 度量 ；② 拼角； ③ 将四边形转化成三角形求内角和
3．在四边形内角和的探索过程中，用到了几种方法，你认为哪种方法好？请讲述你的理由
4．根据四边形的内角和的求法，你能否求出五边形的内角和呢？
方法1：如图1，连结AD、AC，五边形的 内角和为：3×180°=540°
方法2：如图2，连结AC，则五边形内角和 为：360°+180°=540°
方法3：如图3，在AB上任取点F，连FC、FD、FE，则五边形的内角和为：4×180-180°=540°
方法4：如图4，在五边形内任取一点O，连结OA、 OB、OC、OD、OE，则五边形内角和为： 5×180°-360°=540°
方法5：如图5，在AB上任取一点F，连结FD，则五边形的内角和为：2×360°-180°=540°
方法6：如图6，在五边开外任取一点O，连结OA、OB、OC、OD、OE，则五边形内角和为： 4×180°-180°=540°
小结：纵观以上各种证明思路，其共同点是通过图形分割，把五边形问题转化为熟悉的三角形、四边形问题来解决.
5．小组合作，完成下面的表格：
(n-2) × 180°
从多边形的一个顶点可以引出（n-3) 条对角线，把n 边形分成(n-2) 个三角形从而得出：n 边形的内角和是(n-2) ·180°
1．如图，四边形ABCD中，∠A+∠C=180°，∠B与∠D有怎样的关系？
2．一个多边形的内角和为1440°，则它是几边形？
3．一个多边形的边数增加1，则它的内角和将如何变化？
想一想：观察图中的多边形，它们的边、角有什么特点？
正多边形定义：在平面内，每个内角都相等、每条边也都相等的多边形叫做正多边形
议一议：①一个多边形的边都相等，它的内角一定都相等吗？②一个多边形的内角都相等，它的边一定都相等吗？
练一练：①正三角形、正四边形（正方形）、正五边形、正六边形、正八边形的内角分别是多少度？②正n 边形的内角是多少度？③一个正多边形的每个内角都是150°，求它的边数 ？
议一议: 剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.