



所属成套资源:人教版数学八上同步提升训练 (2份,原卷版+解析版)
人教版(2024)12.1 全等三角形优秀同步练习题
展开
这是一份人教版(2024)12.1 全等三角形优秀同步练习题,文件包含人教版数学八上同步提升训练专题125全等三角形的证明及计算大题专项训练30道原卷版doc、人教版数学八上同步提升训练专题125全等三角形的证明及计算大题专项训练30道解析版doc等2份试卷配套教学资源,其中试卷共87页, 欢迎下载使用。
考卷信息:
本套训练卷共30题,题型针对性较高,覆盖面广,选题有深度,可深化学生对全等三角形工具的应用及构造全等三角形!
一.解答题(共30小题)
1.(2022•黄州区校级模拟)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
【分析】(1)根据题意和题目中的条件可以找出△ABC≌△ADE的条件;
(2)根据(1)中的结论和等腰直角三角形的定义可以得到∠FAE的度数;
(3)根据题意和三角形全等的知识,作出合适的辅助线即可证明结论成立.
【解答】证明:(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(SAS);
(2)∵∠CAE=90°,AC=AE,
∴∠E=45°,
由(1)知△BAC≌△DAE,
∴∠BCA=∠E=45°,
∵AF⊥BC,
∴∠CFA=90°,
∴∠CAF=45°,
∴∠FAE=∠FAC+∠CAE=45°+90°=135°;
(3)延长BF到G,使得FG=FB,
∵AF⊥BG,
∴∠AFG=∠AFB=90°,
在△AFB和△AFG中,
,
∴△AFB≌△AFG(SAS),
∴AB=AG,∠ABF=∠G,
∵△BAC≌△DAE,
∴AB=AD,∠CBA=∠EDA,CB=ED,
∴AG=AD,∠ABF=∠CDA,
∴∠G=∠CDA,
∵∠GCA=∠DCA=45°,
在△CGA和△CDA中,
,
∴△CGA≌△CDA(AAS),
∴CG=CD,
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.
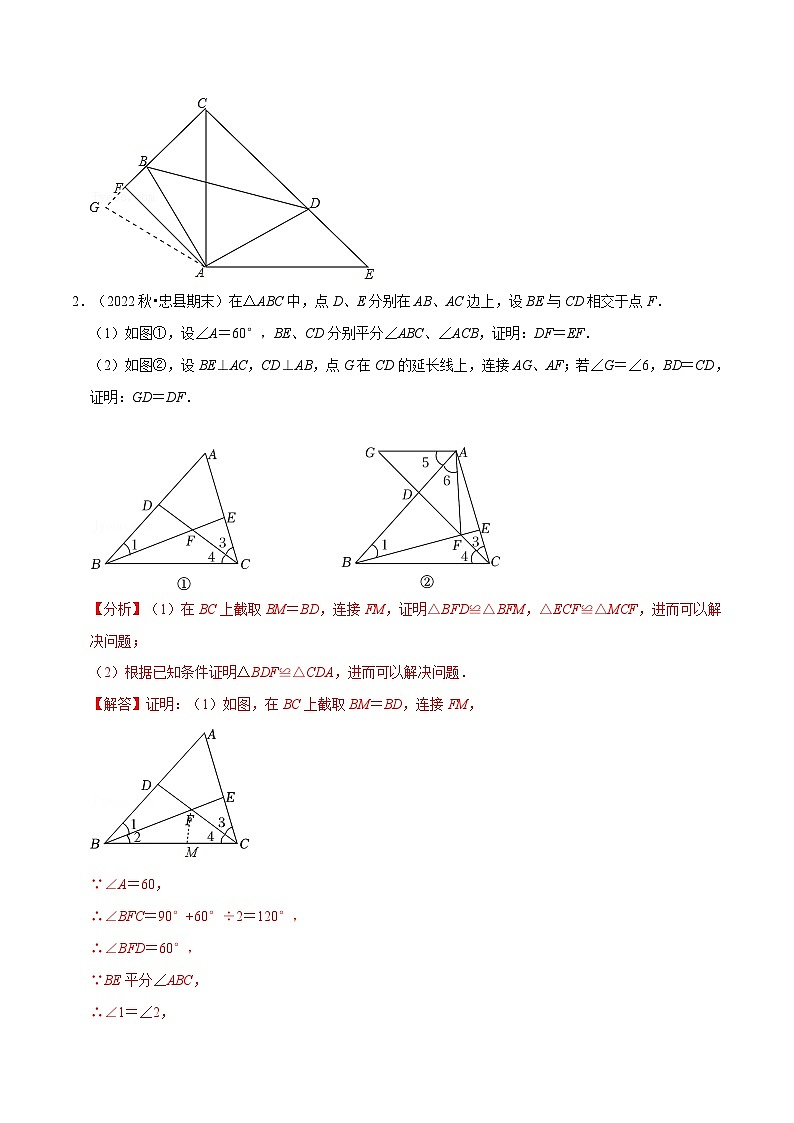
2.(2022秋•忠县期末)在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.
(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.
(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.
【分析】(1)在BC上截取BM=BD,连接FM,证明△BFD≌△BFM,△ECF≌△MCF,进而可以解决问题;
(2)根据已知条件证明△BDF≌△CDA,进而可以解决问题.
【解答】证明:(1)如图,在BC上截取BM=BD,连接FM,
∵∠A=60,
∴∠BFC=90°+60°÷2=120°,
∴∠BFD=60°,
∵BE平分∠ABC,
∴∠1=∠2,
在△BFD和△BFM中,
,
∴△BFD≌△BFM(SAS),
∴∠BFM=∠BFD=60°,DF=MF,
∴∠CFM=120°﹣60°=60°,
∵∠CFE=∠BFD=60°,
∴∠CFM=∠CFE,
∵CD平分∠ACB,
∴∠3=∠4,
又CF=CF,
在△ECF和△MCF中,
,
∴△ECF≌△MCF(ASA),
∴EF=MF,
∴DF=EF;
(2)∵BE⊥AC,CD⊥AB,
∴∠BDF=∠CDA=90°,
∴∠1+∠BFD=90°,∠3+∠CFE=90°,∠BFD=∠CFE,
∴∠1=∠3,
∵BD=CD,
在△BDF和△CDA中,
,
∴△BDF≌△CDA(ASA),
∴DF=DA,
∵∠ADF=90°,
∴∠6=45°,
∵∠G=∠6,
∴∠5=45°
∴∠G=∠5,
∴GD=DA,
∴GD=DF.
3.(2022秋•路北区期中)如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.
(1)证明:AD∥BC.
(2)在移动过程中,小明发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,会出现△DEG与△BFG全等的情况.
【分析】(1)由AD=BC=4,AB=CD,BD为公共边,所以可证得△ABD≌△CDB,所以可知∠ADB=∠CBD,所以AD∥BC;
(2)设运动时间为t,点G的运动速度为v,根据全等三角形的性质进行解答即可.
【解答】(1)证明:在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠CBD,
∴AD∥BC;
(2)解:设运动时间为t,点G的运动速度为v,
当时,
若△DEG≌△BGF,
则,
∴,
∴,
∴v=3;
若△DEG≌△BGF,
则,
∴,
∴(舍去);
当时,
若△DEG≌△BFG,
则,
∴,
∴,
∴;
若△DEG≌△BGF,
则,
∴,
∴,
∴v=1.
综上,当点G的速度为3或1.5或1时.会出现△DEG与△BFG全等的情况.
4.(2022春•北碚区校级期末)如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA=ED.
(1)如图1,若∠A=60°,∠CDE=120°,且CD+AB=BC.求证:CE平分∠BCD;
(2)如图2,∠A与∠D互补,∠DEA=2∠CEB,若凸五边形ABCDE面积为30,且CDAB=4.求点E到BC的距离.
【分析】(1)延长CD到T,使得DT=BA,连接ET.证明△EAB≌△EDT(SAS),△ECB≌△ECT(SSS),可得结论.
(2)延长CD到Q,使得∠QED=∠AEB,过点E作EH⊥BC于H.证明△AEB≌△DEQ(ASA),△ECB≌△ECQ(SAS),由题意S五边形ABCDE=S四边形EBCQ=2S△EBC=30,推出S△EBC=15,再利用三角形面积公式求出EH即可.
【解答】(1)证明:延长CD到T,使得DT=BA,连接ET.
∵∠CDE=120°,
∴∠EDT=180°﹣120°=60°,
∵∠A=60°,
∴∠A=∠EDT,
在△EAB和△EDT中,
,
∴△EAB≌△EDT(SAS),
∴EB=ET,
∴CB=CD+BA=CD+DT=CT,
在△ECB和△ECT中,
,
∴△ECB≌△ECT(SSS),
∴∠ECB=∠ECD,
∴CE平分∠BCD.
(2)解:延长CD到Q,使得∠QED=∠AEB,过点E作EH⊥BC于H.
∵∠A+∠CDE=180°,∠CDE+∠EDQ=180°,
∴∠A=∠EDQ,
在△AEB和△DEQ中,
,
∴△AEB≌△DEQ(ASA),
∴EB=EQ,
∵∠AED=2∠BEC,
∴∠AEB+∠CED=∠BEC,
∴∠CED+∠DEQ=∠BEC,
∴∠CEB=∠CEQ,
在△CEB和△CEQ中,
,
∴△ECB≌△ECQ(SAS),
∵S五边形ABCDE=S四边形EBCQ=2S△EBC=30,
∴S△EBC=15,
∵CDAB=4,
∴AB=6,CD=4,
∴BC=CD+QD=CD+AB=10,
∴10×EH=15,
∴EH=3,
∴点E到BC的距离为3.
5.(2022秋•宜兴市期中)如图,在△ABC中,已知∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,CD与BM相交于点E,且点E是CD的中点,连接MD,过点D作DN⊥MD,交BM于点N.
(1)求证:△DBN≌△DCM;
(2)请探究线段NE、ME、CM之间的数量关系,并证明你的结论.
【分析】(1)根据两角夹边相等的两个三角形全等即可证明.
(2)结论:NE﹣ME=CM.作DF⊥MN于点F,由(1)△DBN≌△DCM 可得DM=DN,由△DEF≌△CEM,推出ME=EF,CM=DF,由此即可证明.
【解答】(1)证明:∵∠ABC=45°,CD⊥AB,
∴∠ABC=∠DCB=45°,
∴BD=DC,
∵∠BDC=∠MDN=90°,
∴∠BDN=∠CDM,
∵CD⊥AB,BM⊥AC,
∴∠ABM=90°﹣∠A=∠ACD,
在△DBN和△DCM中,
,
∴△DBN≌△DCM.
(2)结论:NE﹣ME=CM.
证明:由(1)△DBN≌△DCM 可得DM=DN.
作DF⊥MN于点F,又 ND⊥MD,
∴DF=FN,
在△DEF和△CEM中,
,
∴△DEF≌△CEM,
∴ME=EF,CM=DF,
∴CM=DF=FN=NE﹣FE=NE﹣ME.
6.(2022秋•淅川县期末)如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)示例:在图1中,通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系.
答:AB与AP的数量关系和位置关系分别是 AB=AP 、 AB⊥AP .
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.请你观察、测量,猜想并写出BQ与AP所满足的数量关系和位置关系.答:BQ与AP的数量关系和位置关系分别是 BQ=AP 、 BQ⊥AP .
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
【分析】(1)由于AC⊥BC,且AC=BC,边EF与边AC重合,且EF=FP,则△ABC与△EFP是全等的等腰直角三角形,根据等腰直角三角形的性质得到∠BAC=∠CAP=45°,AB=AP,则∠BAP=90°,于是AP⊥AB;
(2)延长BQ交AP于H点,可得到△QPC为等腰直角三角形,则有QC=PC,根据“SAS”可判断△ACP≌△BCQ,则AP=BQ,∠CAP=∠CBQ,利用三角形内角和定理可得到∠AHQ=∠BCQ=90°,即AP⊥BQ;
(3)BQ与AP所满足的数量关系为相等,位置关系为垂直.证明方法与(2)一样.
【解答】解:(1)AB=AP,AB⊥AP;
(2)BQ=AP,BQ⊥AP;
(3)成立.
证明:如图,∵∠EPF=45°,
∴∠CPQ=45°.
∵AC⊥BC,
∴∠CQP=∠CPQ,
CQ=CP.
在Rt△BCQ和Rt△ACP中,
∴Rt△BCQ≌Rt△ACP(SAS)
∴BQ=AP;
延长QB交AP于点N,
∴∠PBN=∠CBQ.
∵Rt△BCQ≌Rt△ACP,
∴∠BQC=∠APC.
在Rt△BCQ中,∠BQC+∠CBQ=90°,
∴∠APC+∠PBN=90°.
∴∠PNB=90°.
∴QB⊥AP.
7.(2022秋•渝中区校级期中)如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足|4﹣b|=0,
(1)求A、B两点的坐标;
(2)D为OA的中点,连接BD,过点O作OE⊥BD于F,交AB于E,求证:∠BDO=∠EDA;
(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变,求其值;若变化,求线段OQ的取值范围.
【分析】①首先根据已知条件和非负数的性质得到关于a、b的方程,解方程组即可求出a,b的值,也就能写出A,B的坐标;
②作出∠AOB的平分线,通过证△BOG≌△OAE得到其对应角相等解决问题;
③过M作x轴的垂线,通过证明△PBO≌△MPN得出MN=AN,转化到等腰直角三角形中去就很好解决了.
【解答】解:①∵|4﹣b|=0
∴a=4,b=4,
∴A(4,0),B(0,4);
(2)证明:作∠AOB的角平分线,交BD于G,
∴∠BOG=∠OAE=45°,OB=OA,
∠OBG=∠AOE=90°﹣∠BOF,
∴△BOG≌△OAE,
∴OG=AE.
∵∠GOD=∠EAD=45°,OD=AD,
∴△GOD≌△EDA.
∴∠GDO=∠ADE.
(3)过M作MN⊥x轴,垂足为N.
∵∠BPM=90°,
∴∠BPO+∠MPN=90°.
∵∠AOB=∠MNP=90°,
∴∠BPO=∠PMN,∠PBO=∠MPN,
∵BP=MP,
∴△PBO≌△MPN(AAS),
MN=OP,PN=AO=BO,
OP=OA+AP=PN+AP=AN,
∴MN=AN,∠MAN=45°.
∵∠BAO=45°,
∴∠BAO+∠OAQ=90°
∴△BAQ是等腰直角三角形.
∴OB=OQ=4.
∴无论P点怎么动OQ的长不变.
8.(2022春•崇川区校级期末)如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB与y轴交于D点,∠CAO=90°﹣∠BDO.
(1)求证:AC=BC;
(2)在(1)中点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,如图2,求BC+EC的长;
(3)在(1)中,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,(如图3),当点H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
【分析】(1)由题意∠CAO=90°﹣∠BDO,可知∠CAO=∠CBD,CD平分∠ACB与y轴交于D点,所以可由AAS定理证明△ACD≌△BCD,由全等三角形的性质可得AC=BC;
(2)过D作DN⊥AC于N点,可证明Rt△BDO≌Rt△EDN、△DOC≌△DNC,因此,BO=EN、OC=NC,所以,BC+EC=BO+OC+NC﹣NE=2OC,即可得BC+EC的长;
(3)在x轴的负半轴上取OM=FH,可证明△DFH≌△DOM、△HDG≌△MDG,因此,MG=GH,所以,GH=OM+OG=FH+OG,即可证明所得结论.
【解答】(1)证明:∵∠CAO=90°﹣∠BDO,
∴∠CAO=∠CBD.
在△ACD和△BCD中
,
∴△ACD≌△BCD(AAS).
∴AC=BC.
(2)解:由(1)知∠CAD=∠DEA=∠DBO,
∴BD=AD=DE,过D作DN⊥AC于N点,如右图所示:
∵∠ACD=∠BCD,
∴DO=DN,
在Rt△BDO和Rt△EDN中
,
∴Rt△BDO≌Rt△EDN(HL),
∴BO=EN.
在△DOC和△DNC中,
∴△DOC≌△DNC(AAS),
可知:OC=NC;
∴BC+EC=BO+OC+NC﹣NE=2OC=8.
(3)GH=FH+OG.
证明:由(1)知:DF=DO,
在x轴的负半轴上取OM=FH,连接DM,如右图所示:
在△DFH和△DOM中
,
∴△DFH≌△DOM(SAS).
∴DH=DM,∠1=∠ODM.
∴∠GDH=∠1+∠2=∠ODM+∠2=∠GDM.
在△HDG和△MDG中
,
∴△HDG≌△MDG(SAS).
∴MG=GH,
∴GH=OM+OG=FH+OG.
9.(2022秋•莆田期中)如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,
(1)求C点的坐标;
(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP﹣DE的值;
(3)如图3,已知点F坐标为(﹣2,﹣2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①m﹣n为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.
【分析】(1)要求点C的坐标,则求C的横坐标与纵坐标,因为AC=AB,则作CM⊥x轴,即求CM和AM的值,容易得△MAC≌△OBA,根据已知即可求得C点的值;
(2)求OP﹣DE的值则将其放在同一直线上,过D作DQ⊥OP于Q点,即是求PQ的值,由图易求得△AOP≌△PDQ(AAS),即可求得PQ的长;
(3)利用(2)的结论,可知m+n为定长是正确的,过F分别作x轴和y轴的垂线,类似(2),即可求得m+n的值.
【解答】解:(1)过C作CM⊥x轴于M点,如图1,
∵CM⊥OA,AC⊥AB,
∴∠MAC+∠OAB=90°,∠OAB+∠OBA=90°
则∠MAC=∠OBA
在△MAC和△OBA中,
则△MAC≌△OBA(AAS)
则CM=OA=2,MA=OB=4,则点C的坐标为(﹣6,﹣2);
(2)过D作DQ⊥OP于Q点,如图2,则OP﹣DE=PQ,∠APO+∠QPD=90°
∠APO+∠OAP=90°,则∠QPD=∠OAP,
在△AOP和△PDQ中,
则△AOP≌△PDQ(AAS)
∴OP﹣DE=PQ=OA=2;
(3)结论②是正确的,m+n=﹣4,
如图3,过点F分别作FS⊥x轴于S点,FT⊥y轴于T点,
则FS=FT=2,∠FHS=∠HFT=∠FGT,
在△FSH和△FTG中,
则△FSH≌△FTG(AAS)
则GT=HS,
又∵G(0,m),H(n,0),点F坐标为(﹣2,﹣2),
∴OT=OS=2,OG=|m|=﹣m,OH=n,
∴GT=OG﹣OT=﹣m﹣2,HS=OH+OS=n+2,
则﹣2﹣m=n+2,
则m+n=﹣4.
10.(2022秋•南岗区校级月考)在△ABC中,AB=AC,BD⊥AC于点D,BE平分∠ABD,点F在BD上,∠BEF=45°
(1)如图1,求证:BF=CE;
(2)如图2,作EM⊥BE,交BC的延长线于点M,连接AM,交BE的延长线于点N,若∠BAC=30°,请探究线段EF与MN的数量关系,并加以证明.
【分析】(1)在AB上截取BG=BF,连接EG,利用BE平分∠ABD,可得∠GBE=∠FBE,根据题意易求证△BGE≌△BFE(SAS),设∠EBG=∠EBF=α,∠DBC=β,根据角度关系可求证GE∥BC,通过等量代换即可求解;
(2)数量关系为:MN=2EF,理由为连接NC,根据题意可求证BE=EM,∠EBF=∠CEM=30°,BF=CE,从而求证△BEF≌△EMC(SAS),可得EF=MC,即可求解.
【解答】(1)证明:如图,在AB上截取BG=BF,连接EG,
∵BE平分∠ABD,
∴∠GBE=∠FBE,
∵BG=BF,BE=BE,
∴△BGE≌△BFE(SAS),
∴∠GEB=∠FEB=45°,
设∠EBG=∠EBF=α,∠DBC=β,
∴∠AGE=∠GBE+∠GEB=45°+α,
∵AB=AC,
∴∠C=∠ABC=2α+β,
∵∠BDC=90°,
∴∠DBC+∠C=90°,即2α+β+β=90°,
∴α+β=90°,
∴∠ABC=2α+β=45°+α,
∴∠ABC=∠AGE,
∴GE∥BC,
∴∠AEG=∠C=∠ABC=∠AGE,
∴AG=AE,
∴AB﹣AG=AC﹣AE,即BG=CE,
∵BF=BG,
∴BF=CE;
(2)解:数量关系为:MN=2EF,理由如下:
∵∠BAC=30°,AB=AC,
∴∠ABC=∠ACB=75°,
∵BD⊥AC,
∴∠DBC=90°﹣75°=15°,
∴∠ABD=75°﹣15°=60°,
∵BE平分∠ABD,
∴∠ABE=∠EBD=30°,
∴∠BAC=∠ABE=30°,
∴AE=BE,
∴∠BED=∠BAC+∠ABE=75°,
∴∠EMC=45°,
∵∠EBM=∠EBD+∠DBC=45°,
∴∠EMC=∠EBM=45°,
∴BE=EM,
∴EM=AE,
∴∠EAM=∠EMA∠CEM=15°,
∴∠AMC=∠EMC+∠AME=60°=∠BEC,
如图,连接NC,
∴E、N、M、C四点共圆,
∴∠NCM=∠NEM=90°,
在Rt△NMC中,∠NMC=60°,
∴∠CNM=30°,
∴CMMN,
∵BE=EM,∠EBF=∠CEM=30°,BF=CE,
∴△BEF≌△EMC(SAS),
∴EF=MC,
∴MN=2EF.
11.(2022春•运城期末)综合与探究
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD.
(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.
【分析】(1)可利用SAS证明结论;
(2)由全等三角形的性质可得∠AEC=∠ADB,结合平角的定义可得∠DAE+∠DFE=180°,根据∠BFC+∠DFE=180°,可求得∠BFC=∠DAE,即可求解;
(3)连接AF,过点A作AJ⊥CF于点J.结合全等三角形的性质利用HL证明Rt△AFJ≌Rt△AFH,Rt△AJE≌Rt△AHD可得FJ=FH,EJ=DH,进而可证明结论.
【解答】(1)证明:∵∠BAC=∠DAE.
∴∠CAE=∠BAD.
在△ACE和△ABD中,
,
∴△ACE≌△ABD(SAS);
(2)解:∵△ACE≌△ABD,
∴∠AEC=∠ADB,
∴∠AEF+∠AEC=∠AEF+∠ADB=180°.
∴∠DAE+∠DFE=180°,
∵∠BFC+∠DFE=180°,
∴∠BFC=∠DAE=∠BAC=50°;
(3)证明:如图,连接AF,过点A作AJ⊥CF于点J.
∵△ACE≌△ABD,
∴S△ACE=S△ABD,CE=BD,
∵AJ⊥CE,AH⊥BD.
∴,
∴AJ=AH.
在Rt△AFJ和Rt△AFH中,
,
∴Rt△AFJ≌Rt△AFH(HL),
∴FJ=FH.
在Rt△AJE和Rt△AHD中,
,
∴Rt△AJE≌Rt△AHD(HL),
∴EJ=DH,
∴EF+DH=EF+EJ=FJ=FH.
12.(2022秋•松桃县期末)如图①:△ABC中,AC=BC,延长AC到E,过点E作EF⊥AB交AB的延长线于点F,延长CB到G,过点G作GH⊥AB交AB的延长线于H,且EF=GH.
(1)求证:△AEF≌△BGH;
(2)如图②,连接EG与FH相交于点D,若AB=4,求DH的长.
【分析】(1)利用AAS即可证明△AEF≌△BGH;
(2)结合(1)证明△EFD≌△GHD,即可解决问题.
【解答】(1)证明:∵AC=BC,
∴∠A=∠ABC.
∵∠ABC=∠GBH,
∴∠A=∠GBH.
∵EF⊥AB,GH⊥AB,
∴∠AFE=∠BHG.
在△ADG和△CDF中,
,
∴△AEF≌△BGH(AAS).
(2)解:∵△AEF≌△BGH,
∴AF=BH,
∴AB=FH=4.
∵EF⊥AB,GH⊥AB,
∴∠EFD=∠GHD.
在△EFD和△GHD中,
∴△EFD≌△GHD(AAS),
∴.
13.(2022秋•两江新区期末)在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.
(1)求证:AB=BD;
(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.
【分析】(1)证明Rt△ACB≌Rt△DEB即可解决问题;
(2)作BM平分∠ABD交AK于点M,证明△BMK≌△BGK,△ABM≌△DBG,即可解决问题.
【解答】证明:(1)在Rt△ACB和Rt△DEB中,
,
∴Rt△ACB≌Rt△DEB(HL),
∴AB=BD,
(2)如图:作BM平分∠ABD交AK于点M,
∵BM平分∠ABD,KB平分∠AKG,
∴∠ABM=∠MBD=45°,∠AKB=∠BKG,
∵∠ABF=∠DBG=45°
∴∠MBD=∠GBD,
在△BMK和△BGK中,
,
∴△BMK≌△BGK(ASA),
∴BM=BG,MK=KG,
在△ABM和△DBG中,
,
∴△ABM≌△DBG(SAS),
∴AM=DG,
∵AK=AM+MK,
∴AK=DG+KG.
14.(2022春•济南期末)如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;
(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.
【分析】(1)利用SAS证明△BCE≌△ACD,根据全等三角形的对应边相等得到AD=BE.
(2)根据△BCE≌△ACD,得到∠EBC=∠DAC,由∠BDP=∠ADC,得到∠BPD=∠DCA=90°,利用等腰三角形的三线合一,即可得到AD平分∠BAE;
(3)AD⊥BE不发生变化.由△BCE≌△ACD,得到∠EBC=∠DAC,由对顶角相等得到∠BFP=∠AFC,根据三角形内角和为180°,所以∠BPF=∠ACF=90°,即AD⊥BE.
【解答】解:(1)∵BC⊥AE,∠BAE=45°,
∴∠CBA=∠CAB,
∴BC=CA,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴AD=BE.
(2)∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BDP=∠ADC,
∴∠BPD=∠DCA=90°,
∵AB=AE,
∴AD平分∠BAE.
(3)AD⊥BE不发生变化.
如图2,
∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BFP=∠AFC,
∴∠BPF=∠ACF=90°,
∴AD⊥BE.
15.(2022春•渭滨区期末)如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C做匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.
(1)试证明:AD∥BC.
(2)在移动过程中,小明发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,△DEG与△BFG全等.
【分析】(1)由AD=BC=4,AB=CD,BD为公共边,所以可证得△ABD≌△CDB,所以可知∠ADB=∠CBD,所以AD∥BC;
(2)设运动时间为t,点G的运动速度为v,根据全等三角形的性质进行解答即可.
【解答】(1)证明:在△ABD和△CDB中
,
∴△ABD≌△CDB,
∴∠ADB=∠CBD,
∴AD∥BC;
(2)解:设运动时间为t,点G的运动速度为v,
当0<t时,若△DEG≌△BFG,则,
∴,
∴,
∴v=3;
若△DEG≌△BGF,则,
∴,
∴ (舍去);
当t时,若△DEG≌△BFG,则,
∴,
∴,
∴v=1.5;
若△DEG≌△BGF,则,
∴,
∴,
∴v=1.
综上,点G的速度为3或1或1.5.
16.(2022秋•宁津县期末)(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.
【分析】(1)由条件可证明△ABD≌△CAE,可得DA=CE,AE=BD,可得DE=BD+CE;
(2)由条件可知∠BAD+∠CAE=180°﹣α,且∠DBA+∠BAD=180°﹣α,可得∠DBA=∠CAE,结合条件可证明△ABD≌△CAE,同(1)可得出结论;
(3)由条件可知EM=AH=GN,可得EM=GN,结合条件可证明△EMI≌△GNI,可得出结论I是EG的中点.
【解答】解:(1)如图1,
∵BD⊥直线l,CE⊥直线l,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)DE=BD+CE.
如图2,
证明如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠DBA=∠CAE,
在△ADB和△CEA中.
.
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE
(3)如图3,
过E作EM⊥HI于M,GN⊥HI的延长线于N.
∴∠EMI=GNI=90°
由(1)和(2)的结论可知EM=AH=GN
∴EM=GN
在△EMI和△GNI中,
,
∴△EMI≌△GNI(AAS),
∴EI=GI,
∴I是EG的中点.
17.(2022秋•富县期中)如图,在△ABC中,∠ACB=60°,D为△ABC边AC上一点,BC=CD,点M在BC的延长线上,CE平分∠ACM,且AC=CE.连接BE交AC于点F,G为边CE上一点,满足CG=CF,连接DG交BE于点H.
(1)求∠DHF的度数;
(2)若EB平分∠DEC,则BE平分∠ABC吗?请说明理由.
【分析】(1)由“SAS”可证△CDG≌△CBF,可得∠CBF=∠CDG,再利用三角形的内角和定理,得∠CBF+∠BCF=∠CDG+∠DHF,又∠ACB=60°,即可出∠DHF=∠ACB=60°,从而问题得以解决;
(2)由“SAS”可证△ABC≌△EDC;由三角形的内角和可得∠DEB+∠EBC=60°,因为∠DEB=∠BEC,只要证出∠DEB+∠ABE=60°,用三角形的外角以及等量代换可以证出,进而得到BE平分∠ABC.
【解答】解:(1)在△CDG和△CBF中,
,
∴△CDG≌△CBF(SAS),
∴∠CBF=∠CDG,
∵∠DFH=∠BFC,
∴∠DHF=∠BCF=60°;
(2)BE平分∠ABC.
理由:∵∠ACB=60°,
∴∠ACM=120°,
∵CE平分∠ACM,
∴∠ACE=∠MCE=60°,
∴∠ACB=∠ACE,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(SAS);
∴∠ABC=∠EDC,
∵∠ACB=∠DCE=60°,
∴∠BEC+∠CBE=60°,
∵∠DFH=∠A+∠ABE=∠BEC+∠FCG,
∵∠A=∠DEC=2∠DEB=2∠BEC,
∴2∠DEB+∠ABE=∠BEC+60°,
∴∠DEB+∠ABE=60°,
∴∠ABE=∠CBE,
∴BE平分∠ABC.
18.(2022秋•台安县月考)如图所示,BD、CE是△ABC的高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究PA与AQ之间的关系;
(2)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
【分析】(1)由条件可得出∠1=∠2,可证得△APB≌△QAC,可得结论;
(2)根据题意画出图形,结合(1)可证得△APB≌△QAC,可得结论.
【解答】(1)结论:AP=AQ,AP⊥AQ
证明:∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAB=90°,∠2+∠CAB=90°,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
而∠DAP+∠P=90°,
∴∠DAP+∠QAC=90°,
即∠QAP=90°,
∴AQ⊥AP;
即AP=AQ,AP⊥AQ;
(2)上述结论成立,理由如下:
如图所示:
∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAE=90°,∠2+∠DAB=90°,
∵∠CAE=∠DAB,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
∵∠PDA=90°,
∴∠P+∠PAD=90°,
∴∠QAC+∠PAD=90°,
∴∠QAP=90°,
∴AQ⊥AP,
即AP=AQ,AP⊥AQ.
19.(2022春•浦东新区期末)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
【分析】(1)延长BD交CE于F,易证△EAC≌△DAB,可得BD=CE,∠ABD=∠ACE,根据∠AEC+∠ACE=90°,可得∠ABD+∠AEC=90°,即可解题;
(2)延长BD交CE于F,易证∠BAD=∠EAC,即可证明△EAC≌△DAB,可得BD=CE,∠ABD=∠ACE,根据∠ABC+∠ACB=90°,可以求得∠CBF+∠BCF=90°,即可解题.
【解答】证明:(1)延长BD交CE于F,
在△EAC和△DAB中,
,
∴△EAC≌△DAB(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠AEC+∠ACE=90°,
∴∠ABD+∠AEC=90°,
∴∠BFE=90°,即EC⊥BD;
(2)延长BD交CE于F,
∵∠BAD+∠CAD=90°,∠CAD+∠EAC=90°,
∴∠BAD=∠EAC,
∵在△EAC和△DAB中,
,
∴△EAC≌△DAB(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ABC+∠ACB=90°,
∴∠CBF+∠BCF=∠ABC﹣∠ABD+∠ACB+∠ACE=90°,
∴∠BFC=90°,即EC⊥BD.
20.(2022春•吉安县期末)课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB的理由是 B .
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是 C .
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
【分析】(1)根据AD=DE,∠ADC=∠BDE,BD=DC推出△ADC和△EDB全等即可;
(2)根据全等得出BE=AC=6,AE=2AD,由三角形三边关系定理得出8﹣6<2AD<8+6,求出即可;
(3)延长AD到M,使AD=DM,连接BM,根据SAS证△ADC≌△MDB,推出BM=AC,∠CAD=∠M,根据AE=EF,推出∠CAD=∠AFE=∠BFD,求出∠BFD=∠M,根据等腰三角形的性质求出即可.
【解答】(1)解:∵在△ADC和△EDB中
,
∴△ADC≌△EDB(SAS),
故选B;
(2)解:∵由(1)知:△ADC≌△EDB,
∴BE=AC=6,AE=2AD,
∵在△ABE中,AB=8,由三角形三边关系定理得:8﹣6<2AD<8+6,
∴1<AD<7,
故选C.
(3)证明:
延长AD到M,使AD=DM,连接BM,
∵AD是△ABC中线,
∴BD=DC,
∵在△ADC和△MDB中
,
∴△ADC≌△MDB(SAS),
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF.
21.(2022秋•立山区期中)如图,已知△ABC中,AB=AC=9cm,BC=6cm,点D为AB的中点.
(1)如果点P在边BC上以1.5cm/s的速度由点B向点C运动,同时,点Q在边CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,经过t秒后,△BPD与△CQP全等,求此时点Q的运动速度与运动时间t.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过 24 秒后,点P与点Q第一次在△ABC的 AC 边上相遇?(在横线上直接写出答案,不必书写解题过程)
【分析】(1)①根据时间和速度分别求得两个三角形中BP、CQ和BD、PC边的长,根据SAS判定两个三角形全等.
②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
(2)根据题意结合图形分析发现:由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走等腰三角形的两个边长.
【解答】解:(1)①全等,理由如下:
∵t=1秒,
∴BP=CQ=1×1.5=1.5(厘米),
∵AB=9cm,点D为AB的中点,
∴BD=4.5cm.
又∵PC=BC﹣BP,BC=6cm,
∴PC=6﹣1.5=4.5(cm),
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BDP和△CPQ中,
,
∴△BPD≌△CQP(SAS);
②假设△BPD与△CQP,
∵vP≠vQ,
∴BP≠CQ,
又由∠B=∠C,则只能是BP=CP=3,BD=CQ=4.5,
∴点P,点Q运动的时间t=BP÷1.5=3÷1.5=2(秒),
∴vQ=CQ÷t=4.5÷2=2.25(cm/s);
(2)设经过x秒后点P与点Q第一次相遇,
由题意,得 2.25x=1.5x+2×9,
解得x=24,
∴点P共运动了24×1.5=36(cm).
∴点P、点Q在AC边上相遇,
∴经过24秒点P与点Q第一次在边AC上相遇.
故答案为:24;AC.
22.(2022秋•太康县期末)如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD、BE.
(1)请你找出图中其他的全等三角形;
(2)试证明CF=EF.
【分析】(1)根据Rt△ABC≌Rt△ADE,得出AC=AE,BC=DE,AB=AD,∠ACB=∠AED,∠BAC=∠DAE,从而推出∠CAD=∠EAB,△ACD≌△AEB,△CDF≌△EBF;
(2)先证得△CDF≌△EBF,进而得到CF=EF.
【解答】解:(1)图中其它的全等三角形为:①△ACD≌△AEB,②△DCF≌△BEF;
①∵Rt△ABC≌Rt△ADE,
∴AC=AE,AB=AD,∠BAC=∠DAE,
∵∠BAC﹣∠BAD=∠DAE﹣∠BAD,
∴∠DAC=∠BAE,
在△ADC和△ABE中
,
∴△ADC≌△ABE(SAS);
②在△DCF和△BEF中
∴△CDF≌△EBF(AAS).
(2)∵Rt△ABC≌Rt△ADE,
∴AC=AE,AD=AB,∠CAB=∠EAD,
∴∠CAB﹣∠DAB=∠EAD﹣∠DAB.
即∠CAD=∠EAB.
∴△CAD≌△EAB,
∴CD=EB,∠ADC=∠ABE.
又∵∠ADE=∠ABC,
∴∠CDF=∠EBF.
又∵∠DFC=∠BFE,
∴△CDF≌△EBF(AAS).
∴CF=EF.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2022/8/9
:23.(2022秋•潮安区期末)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
【分析】(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF=BC+CF=BC+AD,将已知代入即可.
【解答】(1)证明:∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等)
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质);
(2)解:∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF(已证),
∴AB=BC+AD(等量代换)
=5+2=7(cm).
24.(2022秋•黄石期末)已知△ABC和△DEF为等腰三角形,AB=AC,DE=DF,∠BAC=∠EDF,点E在AB上,点F在射线AC上.
(1)如图1,若∠BAC=60°,点F与点C重合,求证:AF=AE+AD;
(2)如图2,若AD=AB,求证:AF=AE+BC.
【分析】(1)由∠BAC=∠EDF=60°,推出△ABC、△DEF为等边三角形,于是得到∠BCE+∠ACE=∠DCA+∠ECA=60°,推出△BCE≌△ACD(SAS),根据全等三角形的性质得到AD=BE,即可得到结论;
(2)在FA上截取FM=AE,连接DM,推出△AED≌△MFD(SAS),根据全等三角形的性质得到DA=DM=AB=AC,∠ADE=∠MDF,证得∠ADM=∠EDF=∠BAC,推出△ABC≌△DAM(SAS),根据全等三角形的性质得到AM=BC,即可得到结论.
【解答】证明:(1)∵∠BAC=∠EDF=60°,
∴△ABC、△DEF为等边三角形,
∴∠BCE+∠ACE=∠DCA+∠ECA=60°,
在△BCE和△ACD中
∴△BCE≌△ACD(SAS),
∴AD=BE,
∴AE+AD=AE+BE=AB=AF;
(2)在FA上截取FM=AE,连接DM,
∵∠BAC=∠EDF,
∴∠AED=∠MFD,
在△AED和△MFD中
,
∴△AED≌△MFD(SAS),
∴DA=DM=AB=AC,∠ADE=∠MDF,
∴∠ADE+∠EDM=∠MDF+∠EDM,
即∠ADM=∠EDF=∠BAC,
在△ABC和△DAM中,
,
∴△ABC≌△DAM(SAS),
∴AM=BC,
∴AE+BC=FM+AM=AF.
即AF=AE+BC.
25.(2022春•济南期中)把两个全等的直角三角板的斜边重合,组成一个四边形ACBD以D为顶点作∠MDN,交边AC、BC于M、N.
(1)若∠ACD=30°,∠MDN=60°,当∠MDN绕点D旋转时,AM、MN、BN三条线段之间有何种数量关系?证明你的结论;
(2)当∠ACD+∠MDN=90°时,AM、MN、BN三条线段之间有何数量关系?证明你的结论;
(3)如图③,在(2)的条件下,若将M、N改在CA、BC的延长线上,完成图3,其余条件不变,则AM、MN、BN之间有何数量关系(直接写出结论,不必证明)
【分析】(1)延长CB到E,使BE=AM,证△DAM≌△DBE,推出∠BDE=∠MDA,DM=DE,证△MDN≌△EDN,推出MN=NE即可;
(2)延长CB到E,使BE=AM,证△DAM≌△DBE,推出∠BDE=∠MDA,DM=DE,证△MDN≌△EDN,推出MN=NE即可;
(3)在CB截取BE=AM,连接DE,证△DAM≌△DBE,推出∠BDE=∠MDA,DM=DE,证△MDN≌△EDN,推出MN=NE即可.
【解答】
(1)AM+BN=MN,
证明:延长CB到E,使BE=AM,
∵∠A=∠CBD=90°,
∴∠A=∠EBD=90°,
在△DAM和△DBE中
,
∴△DAM≌△DBE,
∴∠BDE=∠MDA,DM=DE,
∵∠MDN=∠ADC=60°,
∴∠ADM=∠NDC,
∴∠BDE=∠NDC,
∴∠MDN=∠NDE,
在△MDN和△EDN中
,
∴△MDN≌△EDN,
∴MN=NE,
∵NE=BE+BN=AM+BN,
∴AM+BN=MN.
(2)AM+BN=MN,
证明:延长CB到E,使BE=AM,连接DE,
∵∠A=∠CBD=90°,
∴∠A=∠DBE=90°,
∵∠CDA+∠ACD=90°,∠MDN+∠ACD=90°,
∴∠MDN=∠CDA,
∵∠MDN=∠BDC,
∴∠MDA=∠CDN,∠CDM=∠NDB,
在△DAM和△DBE中
,
∴△DAM≌△DBE,
∴∠BDE=∠MDA=∠CDN,DM=DE,
∵∠MDN+∠ACD=90°,∠ACD+∠ADC=90°,
∴∠NDM=∠ADC=∠CDB,
∴∠ADM=∠CDN=∠BDE,
∵∠CDM=∠NDB
∴∠MDN=∠NDE,
在△MDN和△EDN中
,
∴△MDN≌△EDN,
∴MN=NE,
∵NE=BE+BN=AM+BN,
∴AM+BN=MN.
(3)BN﹣AM=MN,
证明:在CB截取BE=AM,连接DE,
∵∠CDA+∠ACD=90°,∠MDN+∠ACD=90°,
∴∠MDN=∠CDA,
∵∠ADN=∠ADN,
∴∠MDA=∠CDN,
∵∠B=∠CAD=90°,
∴∠B=∠DAM=90°,
在△DAM和△DBE中
,
∴△DAM≌△DBE,
∴∠BDE=∠ADM=∠CDN,DM=DE,
∵∠ADC=∠BDC=∠MDN,
∴∠MDN=∠EDN,
在△MDN和△EDN中
,
∴△MDN≌△EDN,
∴MN=NE,
∵NE=BN﹣BE=BN﹣AM,
∴BN﹣AM=MN.
26.(2022春•城关区校级期末)如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
【分析】根据SAS可知:在∠MON的两边上以O为端点截取相等的两条线段,另外两个端点与角平分线上任意一点相连,所构成的两个三角形全等,它们关于OP对称.
(1)根据三角形内角和定理可求∠BAC.∠EFA是△ACF的外角,根据外角的性质计算求解;
(2)根据图1的作法,在AC上截取AG=AE,则EF=FG;根据ASA证明△FCD≌△FCG,得DF=FG,故判断EF=FD;
(3)只要∠B的度数不变,结论仍然成立.证明同(2).
【解答】解:(1)如图2,∵∠ACB=90°,∠B=60°.
∴∠BAC=30°,
∵AD、CE分别是∠BAC和∠BCA的平分线,
∴∠DAC∠BAC=15°,∠ECA∠ACB=45°.
∴∠EFA=∠DAC+∠ECA=15°+45°=60°.
(2)FE=FD.
如图2,在AC上截取AG=AE,连接FG.
∵AD是∠BAC的平分线,
∴∠EAF=∠GAF,
在△EAF和△GAF中
∵
∴△EAF≌△GAF(SAS),
∴FE=FG,∠EFA=∠GFA=60°,
∴∠GFC=180°﹣60°﹣60°=60°.
又∵∠DFC=∠EFA=60°,
∴∠DFC=∠GFC,
在△FDC和△FGC中
∵
∴△FDC≌△FGC(ASA),
∴FD=FG.
∴FE=FD.
(3)(2)中的结论FE=FD仍然成立.
同(2)可得△EAF≌△HAF,
∴FE=FH,∠EFA=∠HFA,
又由(1)知∠FAC∠BAC,∠FCA∠ACB,
∴∠FAC+∠FCA(∠BAC+∠ACB)(180°﹣∠B)=60°.
∴∠AFC=180°﹣(∠FAC+∠FCA)=120°.
∴∠EFA=∠HFA=180°﹣120°=60°,
同(2)可得△FDC≌△FHC,
∴FD=FH.
∴FE=FD.
27.(2022秋•长寿区期末)如图,△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,EB=EC过点E作EF⊥AC于F,EG⊥AD于G.
(1)请你在不添加辅助线的情况下找出一对你认为全等的三角形,并加以证明;
(2)若AB=3,AC=5,求AF的长.
【分析】已知AE平分∠CAD,EF⊥AC,EG⊥AD及公共边AE,则利用AAS判定△EGA≌△EFA;由△EGA≌△EFA可得到EG=EF,AG=AF,根据HL可判定Rt△EGB≌Rt△EFC,从而得到BG=CF,整理可得到2AF=AC﹣AB,从而可求得AF的长.
【解答】解:(1)△EGA≌△EFA(或△EGB≌△EFC).
证明:∵AE平分∠CAD,
∴∠EAG=∠EAF.
又∵EF⊥AC,EG⊥AD,
∴∠EGA=∠EFA=90°.
在△AEG和△EFA中:
∠EAG=∠EAF,∠EGA=∠EFA,AE=AE,
∴△EGA≌△EFA(AAS).
证明:(2)∵AE平分∠CAD且EF⊥AC,EG⊥AD,
∴EG=EF,∠EGB=∠EFC=90°.
在Rt△EGB和Rt△EFC中
.
∴Rt△EGB≌Rt△EFC(HL).
∴BG=CF.(10分)
又∵BG=AB+AG,CF=AC﹣AF,
即AB+AG=AC﹣AF,
又∵△EGA≌△EFA,
∴AG=AF.
∴2AF=AC﹣AB=5﹣3=2.
∴AF=1.
28.(2022秋•呼和浩特期中)如图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,
(1)图中EC、BF有怎样的数量和位置关系?试证明你的结论.
(2)连接AM,求证:MA平分∠EMF.
【分析】(1)先由条件可以得出∠EAC=∠BAE,再证明△EAC≌△BAF就可以得出结论;
(2)作AP⊥CE于P,AQ⊥BF于Q.由△EAC≌△BAF,推出AP=AQ(全等三角形对应边上的高相等).由AP⊥CE于P,AQ⊥BF于Q,可得AM平分∠EMF;
【解答】(1)解:结论:EC=BF,EC⊥BF.
理由:∵AE⊥AB,AF⊥AC,
∴∠EAB=∠CAF=90°,
∴∠EAB+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠BAF.
在△EAC和△BAF中,
,
∴△EAC≌△BAF(SAS),
∴EC=BF.∠AEC=∠ABF
∵∠AEG+∠AGE=90°,∠AGE=∠BGM,
∴∠ABF+∠BGM=90°,
∴∠EMB=90°,
∴EC⊥BF.
∴EC=BF,EC⊥BF.
(2)证明:作AP⊥CE于P,AQ⊥BF于Q.
∵△EAC≌△BAF,
∴AP=AQ(全等三角形对应边上的高相等).
∵AP⊥CE于P,AQ⊥BF于Q,
∴AM平分∠EMF.
29.(2022秋•句容市校级月考)把两个含有45°角的大小不同的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.说明:AF⊥BE.
【分析】可通过全等三角形将相等的角进行转换来得出结论.本题中我们可通过证明三角形BEC和ACD全等得出∠FBD=∠CAD,根据∠CAD+∠CDA=90°,而∠BDF=∠ADC,因此可得出∠BFD=90°,进而得出结论.那么证明三角形BEC和ACD全等就是解题的关键,两直角三角形中,EC=CD,BC=AC,两直角边对应相等,因此两三角形就全等了.
【解答】证明:AF⊥BE,理由如下:
由题意可知∠DEC=∠EDC=45°,∠CBA=∠CAB=45°,
∴EC=DC,BC=AC,又∠DCE=∠DCA=90°,
∴△ECD和△BCA都是等腰直角三角形,
∴EC=DC,BC=AC,∠ECD=∠ACB=90°.
在△BEC和△ADC中
EC=DC,∠ECB=∠DCA,BC=AC,
∴△BEC≌△ADC(SAS).
∴∠EBC=∠DAC.
∵∠DAC+∠CDA=90°,∠FDB=∠CDA,
∴∠EBC+∠FDB=90°.
∴∠BFD=90°,即AF⊥BE.
30.(2022春•雅安期末)如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
【分析】(1)利用线段的垂直平分线的性质即可证明;
(2)①易证BD=AD,可得△ADC≌△BDC,即可求得∠ACD=∠BCD=45°即可解题;
②连接MC,易证△MCD为等边三角形,即可证明△BDC≌△EMC即可解题;
③分三种情形讨论即可;
【解答】(1)证明:∵CB=CA,DB=DA,
∴CD垂直平分线段AB,
∴CD⊥AB.
(2)①证明:∵AC=BC,
∴∠CBA=∠CAB,
又∵∠ACB=90°,
∴∠CBA=∠CAB=45°,
又∵∠CAD=∠CBD=15°,
∴∠DBA=∠DAB=30°,
∴∠BDE=30°+30°=60°,
∵AC=BC,∠CAD=∠CBD=15°,BD=AD,
在△ADC和△BDC中,
,
∴△ADC≌△BDC(SAS),
∴∠ACD=∠BCD=45°,
∴∠CDE=60°,
∵∠CDE=∠BDE=60°,
∴DE平分∠BDC;
②解:结论:ME=BD,
理由:连接MC,
∵DC=DM,∠CDE=60°,
∴△MCD为等边三角形,
∴CM=CD,
∵EC=CA,∠EMC=120°,
∴∠ECM=∠BCD=45°
在△BDC和△EMC中,
,
∴△BDC≌△EMC(SAS),
∴ME=BD.
③当EN=EC时,∠ENC=7.5°或82.5°;当EN=CN时,∠ENC=150°;当CE=CN时,∠CNE=15°,
所以∠CNE的度数为7.5°、15°、82.5°、150°.
相关试卷
这是一份人教版数学八上同步提升训练专题11.6 角度计算的综合大题专项训练(30道)(2份,原卷版+解析版),文件包含人教版数学八上同步提升训练专题116角度计算的综合大题专项训练30道原卷版doc、人教版数学八上同步提升训练专题116角度计算的综合大题专项训练30道解析版doc等2份试卷配套教学资源,其中试卷共90页, 欢迎下载使用。
这是一份人教版数学八上同步提升训练专题11.5 角度计算中的经典模型【八大题型】(2份,原卷版+解析版),文件包含人教版数学八上同步提升训练专题115角度计算中的经典模型八大题型人教版原卷版doc、人教版数学八上同步提升训练专题115角度计算中的经典模型八大题型人教版解析版doc等2份试卷配套教学资源,其中试卷共76页, 欢迎下载使用。
这是一份初中数学人教版(2024)八年级上册14.1.4 整式的乘法精品达标测试,文件包含人教版数学八上同步提升训练专题142整式的乘法十大题型原卷版doc、人教版数学八上同步提升训练专题142整式的乘法十大题型解析版doc等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。










