




所属成套资源:沪教版(2020)数学必修第二册同步课件
沪教版(2020)必修第二册9.2 复数的几何意义获奖课件ppt
展开
这是一份沪教版(2020)必修第二册9.2 复数的几何意义获奖课件ppt,共33页。PPT课件主要包含了课堂练习,课堂小结等内容,欢迎下载使用。
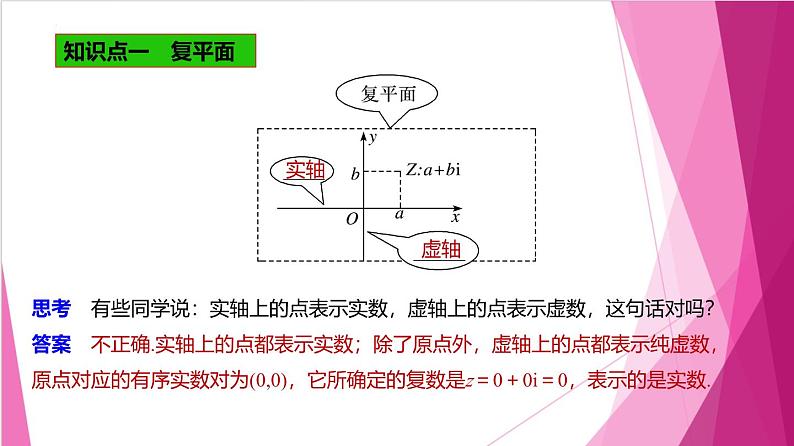
思考 有些同学说:实轴上的点表示实数,虚轴上的点表示虚数,这句话对吗?答案 不正确.实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数,原点对应的有序实数对为(0,0),它所确定的复数是z=0+0i=0,表示的是实数.
知识点二 复数的几何意义
1.复数z=a+bi(a,b∈R) 复平面内的点Z(a,b).2.复数z=a+bi(a,b∈R) 平面向量 .
1.复平面内的点与复数是一一对应的.( )2.复数的模一定是正实数.( )3.若|z1|=|z2|,则z1=z2.( )4.两个复数互为共轭复数,则它们的模相等.( )
例1 已知复数z=(a2-1)+(2a-1)i,其中a∈R.当复数z在复平面内对应的点Z满足下列条件时,求a的值(或取值范围).(1)在实轴上;
一、复数与复平面内的点的关系
解 若z对应的点Z在实轴上,
解 若z对应的点Z在第三象限,
利用复数与点的对应关系解题的步骤(1)找对应关系:复数的几何表示法即复数z=a+bi(a,b∈R)可以用复平面内的点Z(a,b)来表示,是解决此类问题的根据.(2)列出方程:此类问题可建立复数的实部与虚部应满足的条件,通过解方程(组)或不等式(组)求解.
跟踪训练1 在复平面内,若复数z=(m2-m-2)+(m2-3m+2)i(m∈R)的对应点在虚轴上和实轴负半轴上,分别求复数z.
解 若复数z的对应点在虚轴上,则m2-m-2=0,所以m=-1或m=2,所以z=6i或z=0.若复数z的对应点在实轴负半轴上,
二、复数与复平面内的向量的关系
(2)已知复数1,-1+2i,-3i,6-7i,在复平面内画出这些复数对应的向量;
(3)在复平面内的长方形ABCD的四个顶点中,点A,B,C对应的复数分别是2+3i,3+2i,-2-3i,求点D对应的复数.
故点D对应的复数为-3-2i.
复数与平面向量的对应关系(1)根据复数与平面向量的对应关系,可知当平面向量的起点在原点时,向量的终点对应的复数即为向量对应的复数.反之复数对应的点确定后,从原点引出的指向该点的有向线段,即为复数对应的向量.(2)解决复数与平面向量一一对应的问题时,一般以复数与复平面内的点一一对应为工具,实现复数、复平面内的点、向量之间的转化.
A.-5+5i B.5-5iC.5+5i D.-5-5i
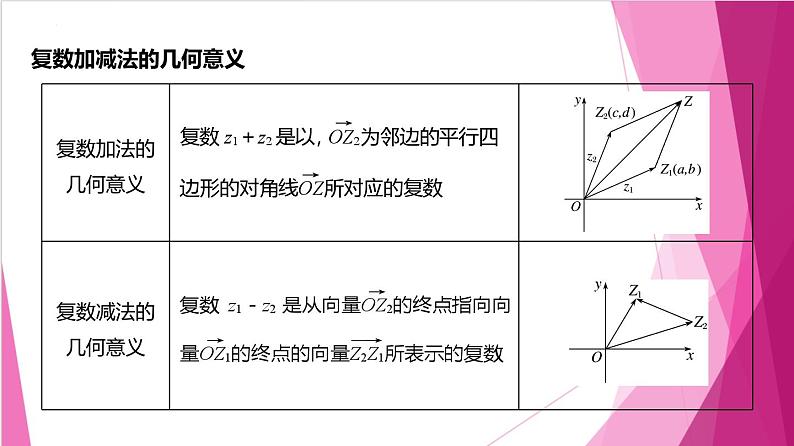
复数加减运算的几何意义
例2 如图所示,平行四边形OABC的顶点O,A,C分别对应的复数为0,3+2i,-2+4i.求:
解 ∵A,C对应的复数分别为3+2i,-2+4i,
向量加法、减法运算的平行四边形法则和三角形法则是复数加法、减法几何意义的依据.利用向量加法“首尾相接”和向量减法“指向被减向量”的特点,在三角形内可求得第三个向量及其对应的复数.注意向量 对应的复数是zB-zA(终点对应的复数减去起点对应的复数).
解 因为ABCD是平行四边形,
而(1+4i)-(3+2i)=-2+2i,
复数加减法几何意义的综合应用
典例 (1)复平面内点A,B,C对应的复数分别为i,1,4+2i,由A→B→C→D按逆时针顺序作▱ABCD,求| |.
解 如图,设D(x,y),F为▱ABCD的对角线的交点,
所以点D对应的复数为z=3+3i,
根据复数加减法的几何意义,
∴∠AOC=30°.同理得∠BOC=30°,∴△OAB为等边三角形,
(1)解决此类问题的关键是由题意正确地画出图形,然后根据三角形法则或平行四边形法则借助复数相等即可求解.(2)复数的几何意义包括三个方面:复数的表示(点和向量)、复数的模的几何意义及复数加减运算的几何意义.复数的几何意义充分体现了数形结合这一重要的数学思想方法,即通过几何图形来研究代数问题.(3)利用图形描述、分析数学问题,建立形与数的联系,提升直观想象的数学核心素养.
例3 (1)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|等于
解析 因为(1+i)x=x+xi=1+yi,
(2)已知复数z满足z+|z|=2+8i,求复数z.
复数模的计算(1)计算复数的模时,应先确定复数的实部和虚部,再利用模长公式计算.虽然两个虚数不能比较大小,但它们的模可以比较大小.(2)设出复数的代数形式,利用模的定义转化为实数问题求解.
跟踪训练3 (1)已知z1=5+3i,z2=5+4i,下列选项中正确的是A.z1>z2B.z1|z2|D.|z1|
相关课件
这是一份高中1复平面与复数的坐标表示获奖教学ppt课件,共20页。PPT课件主要包含了复数的模的几何意义,什么是复平面等内容,欢迎下载使用。
这是一份高中沪教版(2020)1复平面与复数的坐标表示完整版教学课件ppt,共21页。PPT课件主要包含了学习目标,复习引入,情境导入,新课讲解,复数的几何意义1,课本例题,一一对应,复数的几何意义2,2复数的向量表示,补充例题等内容,欢迎下载使用。
这是一份高中数学苏教版 (2019)必修 第二册第12章 复数12.3 复数的几何意义完美版课件ppt,共31页。PPT课件主要包含了复数的几何意义,Za+bi,复数加法的几何意义,复数减法的几何意义等内容,欢迎下载使用。










