高中沪教版（2020）1复平面与复数的坐标表示完整版教学课件ppt

这是一份高中沪教版（2020）1复平面与复数的坐标表示完整版教学课件ppt，共21页。PPT课件主要包含了学习目标，复习引入，情境导入，新课讲解，复数的几何意义1，课本例题，一一对应，复数的几何意义2，２复数的向量表示，补充例题等内容，欢迎下载使用。
1.理解可以用复平面内的点或以原点为起点的向量来表示复数及它们之间的一一对应关系．(重点、难点)2．掌握实轴、虚轴、模等概念．(易混点)3．掌握用向量的模来表示复数的模的方法．(重点)
注：复数如果能比较大小，说明它是实数
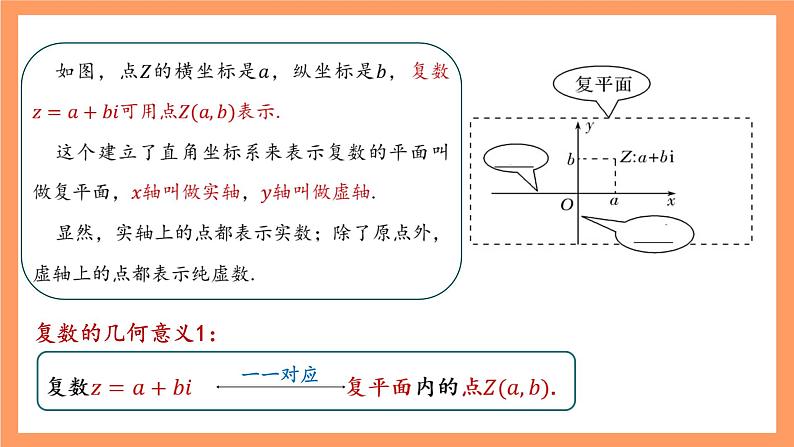
我们知道，实数与数轴上的点一一对应，因此实数可以用数轴上的点来表示，复数有什么几何意义呢？
所以，复数集与平面直角坐标系中的点集之间可以建立一一对应关系，因此可以用点表示复数.
1.复平面与复数的坐标表示
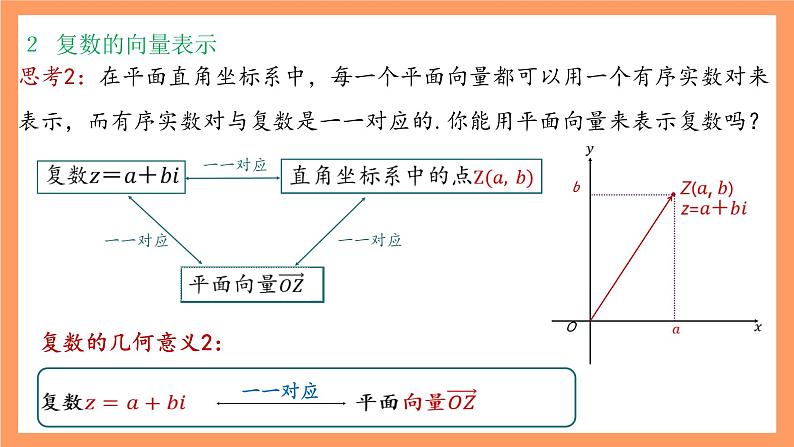
思考2：在平面直角坐标系中，每一个平面向量都可以用一个有序实数对来表示，而有序实数对与复数是一一对应的.你能用平面向量来表示复数吗？
注意，平面上起点不在原点的向量所表示的复数是该向量相应的位置向量所表示的复数．上例说明，这个复数是向量终点对应的复数与起点对应的复数之差．
３ 复数加法的平行四边形法则
我们已经知道向量的加法适用平行四边形法则，在将复数与平面向量建立一一对应后，两个复数的和是否与对应的向量的和一致呢？也就是说，在复平面上是否也可以用平行四边形法则表述复数的加法呢？
——复数与复平面内的点的一 一对应
把点的对应关系转化为实部与虚部应满足的条件.
——复数与复平面向量的一 一对应
当平面向量的起点在原点时，向量的终点对应的复数即为向量对应的复数.
∴ ΔABC是以BC为斜边的直角三角形
对复数和向量的关系理解不透彻，忽略向量平移过程中坐标表示不变.
—— 对复数与向量的关系理解不透彻
解：点A表示的复数是4+3i； 点B表示的复数是3-3i； 点C表示的复数是-3+2i； 点D表示的复数是-3-3i； 点E表示的复数是5； 点F表示的复数是-2； 点G表示的复数是5i； 点H表示的复数是-5i.
1. 说出图中复平面内各点所表示的复数(每个小方格的边长为1).
2. 已知在复平面内，描出表示下列复数的点. (1) 2＋5i；(2) －3＋2i ；(3) 2－4i；(4) －3－i；(5) 5 ；(6) －3i.
2．请你说说复数的几何意义？