









所属成套资源:【新课标大单元】浙教版初数八年级下册课件+教案+大单元整体教学设计
浙教版(2024)八年级下册2.4 一元二次方程根与系数的关系(选学)精品教学课件ppt
展开这是一份浙教版(2024)八年级下册2.4 一元二次方程根与系数的关系(选学)精品教学课件ppt,共30页。PPT课件主要包含了教学目标,复习回顾,探究新知,课堂练习,课堂总结,作业布置,知识技能类作业,必做题,选做题,综合实践类作业等内容,欢迎下载使用。
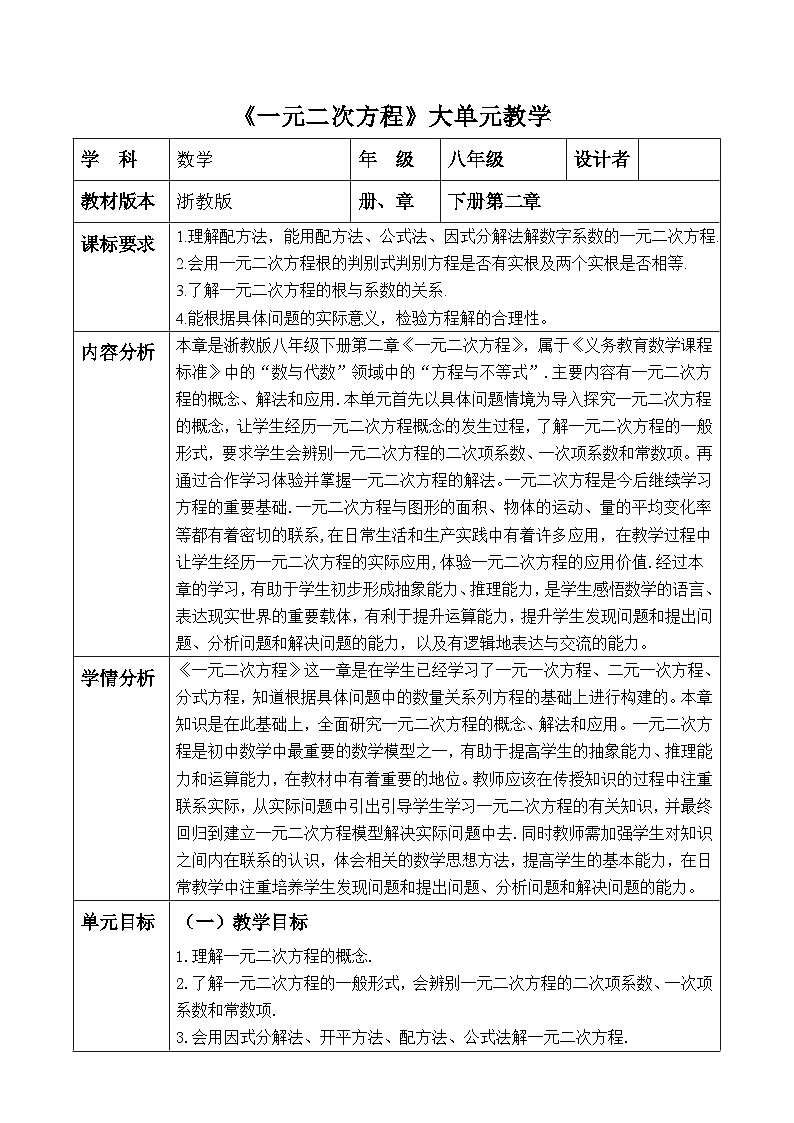
一元二次方程根与系数的关系是“浙教版八年级数学(下)”第二章第四节的内容。本节课的主要内容是探究一元二次方程根与系数的关系,让学生经历一元二次方程根与系数的关系的发现过程,带领学生证明一元二次方程根与系数的关系,要求学生会运用一元二次方程根与系数的关系简化有关一元二次方程根的运算. 一元二次方程根与系数的关系在一元二次方程虽然是选学内容,但是它的内容具有灵活性、应用广泛性、条件放缩性等,有利于锻炼培养学生的逻辑思维能力、灵活解决问题能力等,在教材中有着非常重要的地位和作用.
1.经历一元二次方程根与系数的关系的发现过程.2.了解一元二次方程根与系数的关系及其证明.3.会运用一元二次方程根与系数的关系简化有关一元二次方程根的运算.4.提高分析问题、解决问题的能力及逻辑推理能力.
思考:这些方程的两根之和与两根之积和方程的系数a,b,c有什么联系?
思考:你能证明一元二次方程的根与系数的关系吗?
如果一个一元二次方程的两个根是x1, x2(二次项系数为1),你能写出这个方程吗?
1.下列4个方程中,其中两根互为倒数的是( )A.x2-3x+1=0 B.2x2-3x+1=0 C.x2-3x+2=0 D.x2-3x+3=0
1.若两实数a,b满足a+b=-3,ab=2,则以a,b为根的一元二次方程可以是( )A.x2-3x+2=0 B.x2+3x+2=0 C.x2-3x-2=0 D.x2+3x-2=0
2.若一个等腰三角形的一边为4,另外两边为x2﹣12x+m=0的两根,则m的值为( )A.32B.36C.32或36D.不存在
已知关于x的方程kx2-2(k+1)x+k-1=0有两个不相等的实数根.(1)求k的取值范围;(2)是否存在实数k,使此方程的两个实数根的倒数和等于1? 若存在,求出k的值;若不存在,说明理由.
已知关于x的方程kx2-2(k+1)x+k-1=0有两个不相等的实数根.(2)是否存在实数k,使此方程的两个实数根的倒数和等于1? 若存在,求出k的值;若不存在,说明理由.
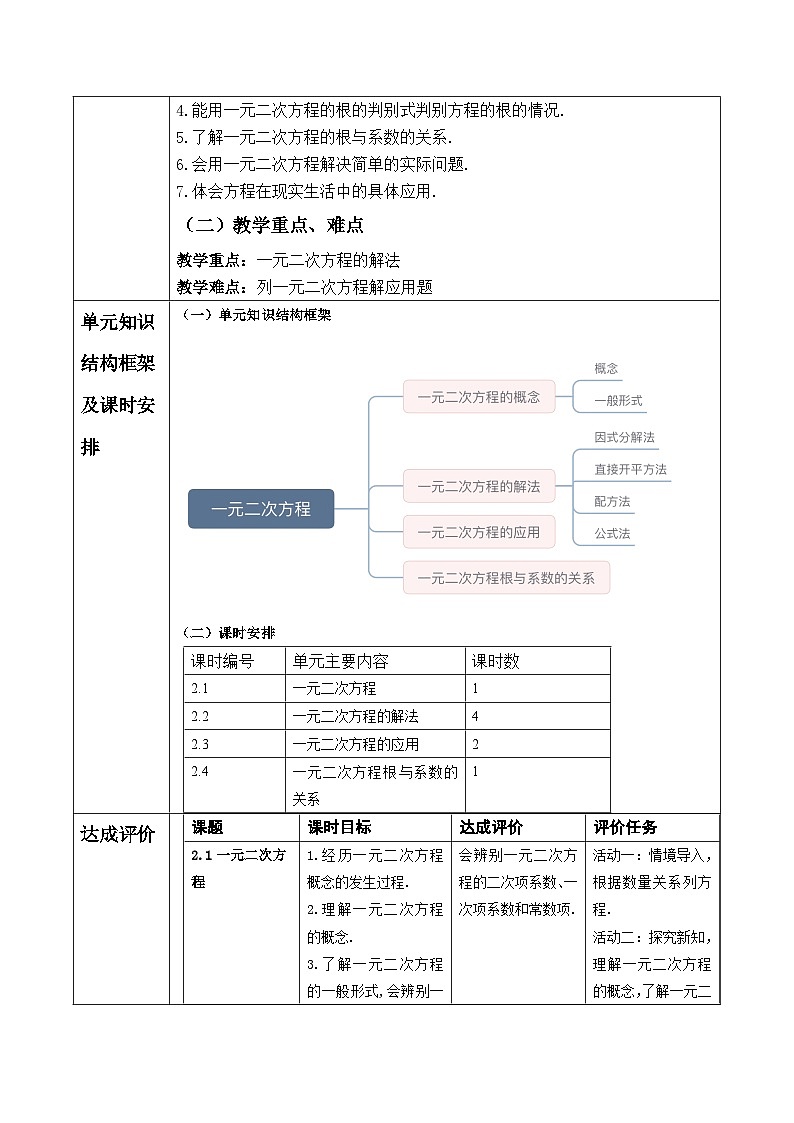
一元二次方程的根与系数有什么关系,它的推论有什么?
1.等腰三角形的一条边长为2,另两边m,n是关于x的一元二次方程x2﹣6x+k﹣1=0的两根,则k的值为( )A.9B.10C.9或10D.8或10
若x1、x2是关于x的一元二次方程x2﹣2(m+1)x+m2+5=0的两个实数根.(1)若(x1﹣1)(x2﹣1)=19,求m的值;(2)已知等腰△ABC的一边长为7,若x1、x2恰好是△ABC另外两边的边长,求这个三角形的周长.
解: (1)根据题意得:x1+x2=2(m+1),x1x2=m2+5,由(x1﹣1)(x2﹣1)=19,整理得:x1x2﹣(x1+x2)+1=19,把x1+x2=2(m+1),x1x2=m2+5代入x1x2﹣(x1+x2)+1=19得:m2+5﹣2(m+1)+1=19,整理得:m2﹣2m﹣15=0,解得:m1=﹣3(不合题意,舍去),m2=5(符合题意),即m的值为5,
若x1、x2是关于x的一元二次方程x2﹣2(m+1)x+m2+5=0的两个实数根.(2)已知等腰△ABC的一边长为7,若x1、x2恰好是△ABC另外两边的边长,求这个三角形的周长.
解:若等腰△ABC的腰长为7,把x=7代入方程x2﹣2(m+1)x+m2+5=0得:49﹣14(m+1)+m2+5=0,解得:m1=4,m2=10,若m1=4,则原方程为:x2﹣10x+21=0,解得:x1=7,x2=3,
续:△ABC三边为7,7,3(符合题意),若m2=10,则原方为:x2﹣22x+105=0,解得:x1=7,x2=15,△ABC三边为7,7,15(不合题意,舍去),若等腰△ABC底长为7,则Δ=[﹣2(m+1)]2﹣4(m2+5)=8m﹣16=0,
续:解得:m=2,原方程为:x2﹣6x+9=0,解得:x1=x2=3,△ABC三边为3,3,7(不合题意,舍去),综上可知:△ABC三边为7,7,3,周长为:7+7+3=17,即这个三角形的周长为17.
相关课件
这是一份数学八年级下册5.3 正方形完美版教学ppt课件,共30页。PPT课件主要包含了教学目标,复习导入,探究新知,课堂练习,课堂总结,作业布置,矩形的性质有什么,菱形的性质有什么,知识技能类作业,必做题等内容,欢迎下载使用。
这是一份初中数学浙教版(2024)八年级下册5.2 菱形精品教学课件ppt,共30页。PPT课件主要包含了教学目标,复习导入,探究新知,课堂练习,课堂总结,作业布置,菱形的概念是什么,知识技能类作业,必做题,选做题等内容,欢迎下载使用。
这是一份初中浙教版(2024)第五章 特殊平行四边形5.2 菱形精品教学ppt课件,共30页。PPT课件主要包含了教学目标,复习导入,探究新知,课堂练习,课堂总结,作业布置,知识技能类作业,必做题,选做题,综合实践类作业等内容,欢迎下载使用。














