

人教版(2024)七年级上册(2024)5.1 方程教案
展开
这是一份人教版(2024)七年级上册(2024)5.1 方程教案,共7页。
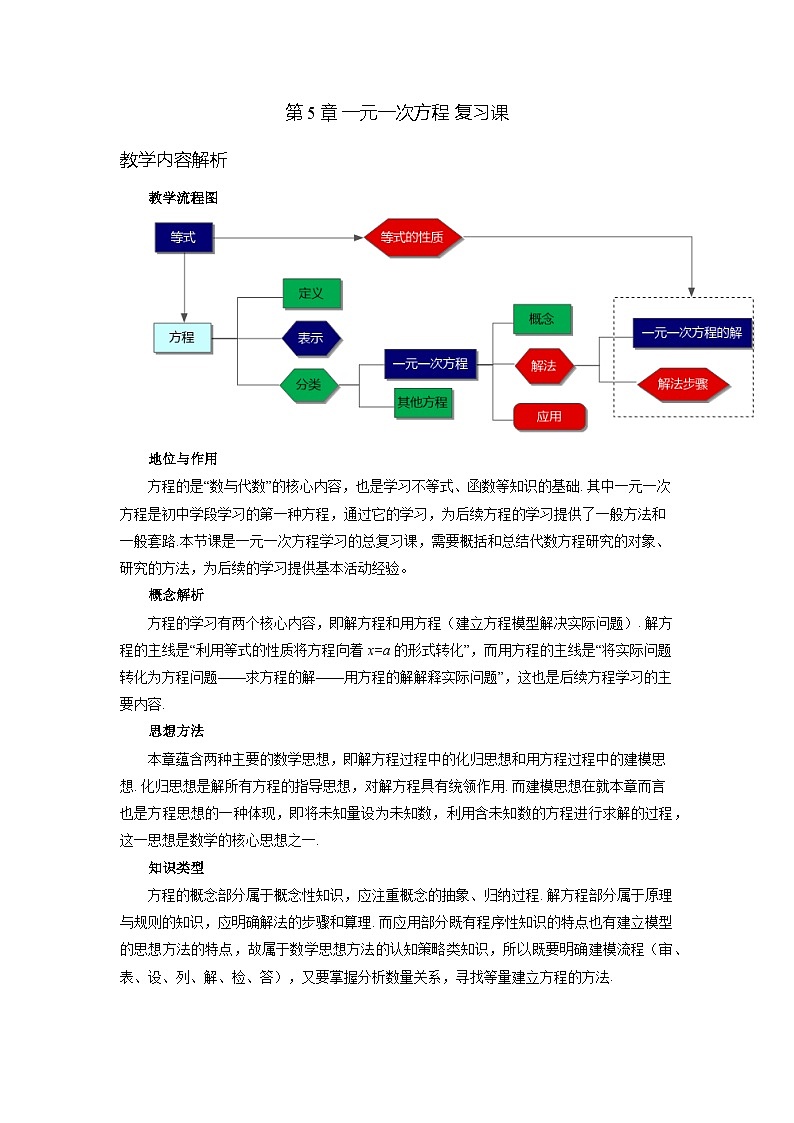
教学流程图
地位与作用
方程的是“数与代数”的核心内容,也是学习不等式、函数等知识的基础. 其中一元一次方程是初中学段学习的第一种方程,通过它的学习,为后续方程的学习提供了一般方法和一般套路.本节课是一元一次方程学习的总复习课,需要概括和总结代数方程研究的对象、研究的方法,为后续的学习提供基本活动经验。
概念解析
方程的学习有两个核心内容,即解方程和用方程(建立方程模型解决实际问题). 解方程的主线是“利用等式的性质将方程向着 x=a 的形式转化”,而用方程的主线是“将实际问题转化为方程问题——求方程的解——用方程的解解释实际问题”,这也是后续方程学习的主要内容.
思想方法
本章蕴含两种主要的数学思想,即解方程过程中的化归思想和用方程过程中的建模思想. 化归思想是解所有方程的指导思想,对解方程具有统领作用. 而建模思想在就本章而言也是方程思想的一种体现,即将未知量设为未知数,利用含未知数的方程进行求解的过程,这一思想是数学的核心思想之一.
知识类型
方程的概念部分属于概念性知识,应注重概念的抽象、归纳过程. 解方程部分属于原理与规则的知识,应明确解法的步骤和算理. 而应用部分既有程序性知识的特点也有建立模型的思想方法的特点,故属于数学思想方法的认知策略类知识,所以既要明确建模流程(审、表、设、列、解、检、答),又要掌握分析数量关系,寻找等量建立方程的方法.
教学重点
本节课的教学重点:一元一次方程知识体系及学习脉络.
教学目标解析
教学目标:
1.了解一元一次方程的整章知识体系.
2.了解学习方程类知识的一般套路.
3.通过对整章知识的整体梳理,体会其中蕴含的数学思想方法.
目标解析:
达成目标1的标志是:能按学习的先后顺序列出本章所学知识点,能画简单的结构图表示它们之间的关系.
达成目标2的标志是:能列举出学习方程的一般套路,即“概念—解法—应用”;总结方程有关概念的学习,体会概念的抽象过程和概括方法;总结方程的解法学习,体会解方程的化归目标和一般划归方法;总结列方程解决应用问题的学习,体会“审设列解答”等应用步骤及相关方法.
达成目标3的标志是:通过对本章知识的整体感知和梳理,体会解方程中蕴含的化归思想和应用问题中蕴含的建模思想.
教学问题诊断分析
具备的基础
通过本章的学习,学生初步掌握了一元一次方程有关的概念、解法和应用,但由于学习的顺序问题,学生对这些知识是逐步认识的,所以对知识的认识带有一定的片面性.
与本课目标的差距分析
在本课的学习中,学生需通过对整章知识的梳理,认识知识间的内在联系,并从整体的角度去认识整章知识,并强化对知识中所蕴含的思想方法的认识,需要学生从碎片化的知识中脱离出来,站在更高的角度去审视知识,并对学生的归纳、梳理能力有一定的要求.
存在的问题:
学生是第一次学习方程,第一次通过建立方程模型解决实际问题。因此可能存在的问题是学生对于代数方程研究的对象和研究的方法不会从整体上加以认识,对于一些原理和方法理解不够到位,运算能力不足导致解题错误,具体问题中找不到等量关系等,这些都是造成学生学习困难的障碍。
应对策略:
针对以上问题,本课应特别注重以下方面:在梳理知识点的环节,应注意以典型例题为载体,通过问题引领知识的学生的知识梳理,并借助结构图的形式强化知识的内在联系;在思想方法的总结环节,还应以典型例题为载体,通过问题引导学生自我总结、自主归纳,教师适当补充、完善.
教学难点
本课的教学难点:对本章知识的整体认识.
教学支持条件分析
运用思维导图工具,引导学生回顾学习过程,逐渐构建本章的知识结构图。通过希沃授课助手等交互平台,充分展露学生的思维过程,在互动交流中完成对本意知识和方法的复习.
教学过程设计
课前检测
请利用思维导图,按学习的先后顺序列举本章所学的内容,并标注每个内容中主要学习的概念、性质和方法.
设计意图:检查学生通过对本章的学习对所学知识的掌握程度,如学生不能列举出基本知识点或列举不完整,可在课前安排学生查阅教材,补充完整.
新课学习
1.问题引领 梳理提升
问题1 举例说明方程与等式的关系以及一元一次方程的特征.
师生活动设计:教师提出问题,学生思考并回答,学生间互相补充,教师引领归纳:1. 方程是等式,但是含有未知数的等式;2. 一元一次方程的特征:只含一个未知数,未知数的最高次为1次,等号的两边都是整式.
追问:我们一般从什么角度对方程进行分类?
师生活动设计:教师追问,学生思考并回答,教师启发学生归纳:对于整式方程,一般按照所含未知数的个数(元)和含未知数项的次数(次)的角度进行分类.
本环节中,教师应重点关注:
(1)学生对方程概念的掌握情况;
(2)学生对整式方程分类的概括能力.
设计意图:在学生掌握一元一次方程概念的基础上,引领学生认识方程的上位概念—等式,及整式方程的分类,使学生在知识体系中认识知识,认识它的上位知识、同类知识,并了解分类原则.
问题2 解方程,并结合解方程的过程说明每一步骤的依据.
师生活动设计:教师出示问题,学生思考并回答.教师提示,学生补充,引导学生归纳出解方程的步骤:去分母(等式的性质),去括号(乘法分配律),移项(等式的性质),合并同类项(乘法分配律),系数化为1(等式的性质).
追问:你能概括一下解一元一次方程的过程吗?
师生活动设计:教师追问,学生尝试概括,互相补充,得到解方程的一般思路:即运用等式性质和运算律,根据方程的具体特点,通过灵活变形将方程逐步化简,最后变为 x=a (已知数)而得解.
本环节中,教师应重点关注:
(1)学生对解方程步骤及其原理的掌握程度;
(2)学生对解方程的一般思路的概括能力.
设计意图:在学生会应用解法解方程的基础上,进一步使学生认识解法步骤的理论依据,应用步骤的指导思想,使学生“知其然亦知其所以然”.
2.例题引领,认识升华
问题3 分析情境,回答问题:一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70 km/h,卡车的行驶速度是60 km/h,客车比卡车早1h经过B地.A,B两地间的路程是多少?
设 A,B两地间的路程是x km,
(1)客车由A到B所用的时间是______________h,卡车由A到B所用的时间是______________h;
(2)由于客车比卡车早1h经过B地,可列方程为______________.
(3)你能说说用字母表示数、列含字母的算式和列方程的区别和联系吗?
师生活动设计:教师提出问题,学生思考回答,教师引导学生归纳:从应用的顺序上看,用字母表示数是基础,之后进一步可以用含字母的算式表示问题中的量,当我们发现相等关系,并用等号将含字母的算式联系起来后,就成为了方程. 但从属性而言,三者分别属于数、式、方程,不应混于一谈.
本环节中,教师应重点关注:
(1)学生对列方程过程的掌握程度;
(2)学生对“用字母表示数、列含字母的算式和列方程的区别和联系”的认识与概括能力.
设计意图:在学生会用字母表示数,会列含字母的算式表示量,并发现相等关系列方程的基础上,以问题引领学生明确三者之间的区别,认识它们的联系,指导学生更明确的运用这三个对象解决问题.
问题4 根据题意列出方程.
(1)某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?设前年购买计算机x台,则可列方程为:______________.
(2)一艘船从甲码头到乙码头顺流而行,用了2 h;从乙码头返回甲码头逆流而行,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的平均速度.设船在静水中的平均速度为x km/h,
则可列方程为:______________.
(3)某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母.1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?设应安排狓名工人生产螺钉,则可列方程为:______________.
师生活动设计:教师提出问题,学生分析解决并回答,互相讨论评价.
追问1:你能说说以上问题中的关键相等关系吗?
师生活动设计:教师提问,师生共同归纳出以结论:
(1)中的关键相等关系是“总量=部分和”;
(2)中的关键相等关系是“顺流航行与逆流航行的路程相等”;
(3)中的关键相等关系是“1个螺钉需要配2个螺母”即“螺母数是螺栓数的2倍”.
追问2:你能再举些例子并说明问题中的关键相等关系吗?
师生活动设计:教师提问,学生讨论、回答、交流.
本环节中,教师应重点关注:
(1)学生对基本应用问题的掌握情况;
(2)学生能否自主举例说明问题中的关键相等关系.
设计意图:“关键相等关系”是列方程解决应用问题的核心所在,以例题引领学生思考、发现、归纳问题中的关键相等关系,并启发学生自主归纳在解决过的问题中,不同情境中的关键相等关系,借此加深学生对关键等量的认识,加强学生对关键等量的重视.
3.绘制图形,系统认知
问题5 请用知识结构图将你在本章学习的知识联系起来.
师生活动设计:教师出示问题,学生操作并小组交流,学生展示交流,反思调整,教师点评.
本环节中,教师应重点关注:
(1)学生能否合理安排各知识点的位置,合理关注知识点之间的联系;
(2)学生能否通过本课的学习适当关注思想与方法层面的知识.
设计意图:在复习知识之后,让学生通过绘制知识结构图对知识有一个整体的认识,将知识梳理为一个完整的体系.
课堂小结
问题6 结合下面的知识结构图,回顾本课内容,回答以下问题:
(1)在本章中,我们分别研究了一元一次方程的哪些方面内容?
(2)我们是怎么研究的?
师生活动设计:教师提问,学生归纳并回答.
本环节中,教师应重点关注:学生对知识的掌握程度,学生对知识的梳理归纳能力.
设计意图:总结提升.
目标检测设计
1.已知是关于x的方程的解.那么a的值是( ).
A. 4 B. 3 C. 2 D. 1
2.已知下列方程:①;②;③;④;⑤.其中一元一次方程有______________,(填序号)你能写出一个二元二次方程吗?______________.
3.解下列方程.
(1);(2).
4.某校九年级学生由学校出发去体育馆参加活动,一部分同学骑自行车先走,过了20分钟后,其余同学乘汽车出发,结果他们同时到达.若骑车同学的速度为15千米/时,汽车的速度是30千米/时,则学校与体育馆距离有多远.
5.一家游泳馆每年6~8月出售夏季会员证,每张会员证80元,只限本人使用,凭证购入场卷每张1元,不凭证购入场卷每张3元. 试讨论并回答:
(1)什么情况下,购会员证与不购证付一样的钱?
(2)什么情况下,购会员证比不购证更合算?
(3)什么情况下,不购会员证比购证更合算?
相关教案
这是一份数学第五章 一元一次方程5.2 解一元一次方程教案及反思,共12页。教案主要包含了教学目标,教学设计等内容,欢迎下载使用。
这是一份初中数学人教版(2024)七年级上册(2024)5.2 解一元一次方程教学设计,共11页。教案主要包含了教学目标,教学设计等内容,欢迎下载使用。
这是一份初中数学人教版(2024)七年级上册(2024)5.2 解一元一次方程教学设计,共11页。教案主要包含了教学目标等内容,欢迎下载使用。










