





苏科版(2024)八年级上册5.2 平面直角坐标系优质课件ppt
展开如何确定直线上点的位置?
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2. 反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了.
如何确定平面上点的位置呢?
5.2.1平面直角坐标系
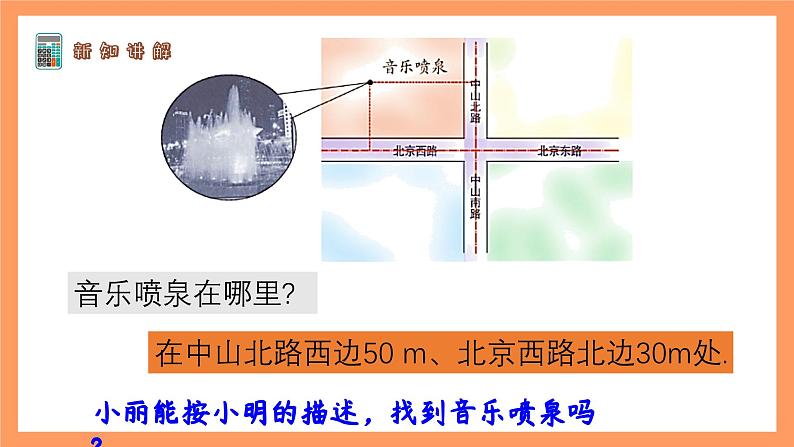
在中山北路西边50 m、北京西路北边30m处.
小丽能按小明的描述,找到音乐喷泉吗?
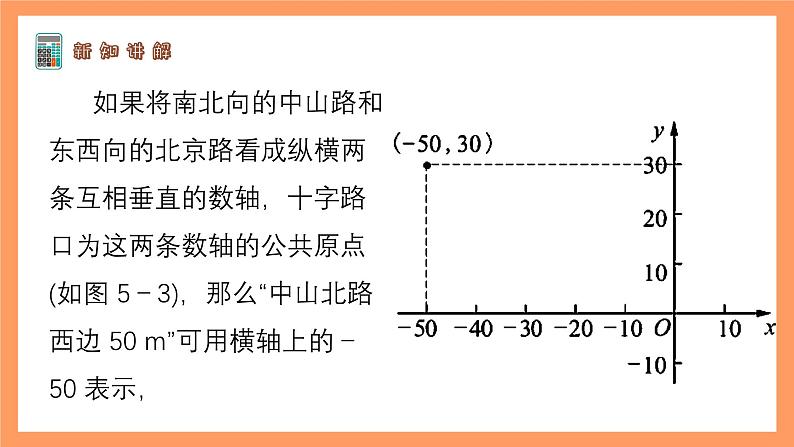
如果将南北向的中山路和东西向的北京路看成纵横两条互相垂直的数轴,十字路口为这两条数轴的公共原点(如图 5-3),那么“中山北路西边 50 m”可用横轴上的-50 表示,
“北京西路北边30m”可用纵轴上的+30 表示,音乐喷泉的位置可以用有序实数对(-50,30)来描述.
知识点 1 平面直角坐标系
平面内两条互相垂直的数轴构成平面直角坐标系,简称为直角坐标系.
水平的数轴称为x轴或横轴,向右为正方向, 铅直方向的数轴称为y轴或纵轴,向上为正方向, 两轴的交点 O 是原点.
1. 平面直角坐标系的两条数轴共原点,且互相垂直; 2. 一般情况下两条坐标轴的单位长度是相等的,在有些实际问题中,两条坐标轴的单位长度可以不相等,但在同一坐标轴上的单位长度必须相等.
下列选项中,平面直角坐标系的画法正确的是 ( )
辨识平面直角坐标系的“四要素”: 1. 两条数轴; 2. 共原点; 3. 单位长度一致; 4. 互相垂直.注意:一般取向上、向右为正方向.
在平面直角坐标系中,用有序实数对(a,b)描述一个点的位置如果将这点记为点 P,那么它的位置可以这样确定: 如图 5-4,过轴上表示实数 a 的点画 x 轴的垂线,过 y 轴上表示实数 b 的点画 y 轴的垂线,这两条垂线的交点即为点 P .
如果 Q 是平面直角坐标系中的一点,你能确定与它相对应的有序实数对吗?
与点Q相应的有序实数对是(m,n).
知识点 2 点的坐标
在平面直角坐标系中,一对有序实数可以确定一个点的位置:反过来,任意一点的位置都可以用一对有序实数来表示. 这样的有序实数对叫做点的坐标.
例如,在图 5-4 中,点P的坐标为(a,b),其中a称为点P的横坐标,b称为点 P 的纵坐标,横坐标写在纵坐标的前面.
点的坐标通常与表示该点的大写字母写在一起,如 P(a,b)、Q(m,n).
(1) 平面直角坐标系内的任意一点,都有唯一的一个有序实数对(点的坐标)与它对应.(2) 任意一个有序实数对(点的坐标)在平面直角坐标系内都有唯一的一点与它对应.
平面直角坐标系内的点与有序实数对的一一对应关系
例1 在平面直角坐标系中,画出下列各点: A (4,1), B(-1,4), C (-4,-2),D (3,-2), E (0,1),F(-4,0).
解: 如图 5-5,过轴上表示4的点画x轴的垂线,过y轴上表示 1的点画 y 轴的垂线,两条垂线的交点为 A(4,1). 同样地,可画出点 B、C、D、E和F.
在如图所示的直角坐标系中,M,N 的坐标分别为( )A. M(2,- 1),N(2,1)B. M(- 1,2),N(2,1)C. M(- 1,2),N(1,2)D. M(2,- 1),N(1,2)
例2 写出图中点 A、B、C 的坐标.
解: 如图,过点A画x 轴的垂线,得点 A的横坐标-4,过点 A 画y轴的垂线,得点 A的纵坐标 3,于是点 A的坐标为(-4,3).
同样地,可得点B、C的坐标分别为(-3,-2)、(1,-3).
知识点 3 象限
如图,两条坐标轴将平面分成的4 个区城称为象限,按逆时针顺序分别记为第一、二、三、四象限. 坐标轴不属于任何象限.
1. 第一象限的点的坐标有什么特点?其他象限的点呢?
第一象限的点的横坐标与纵坐标都为正数;第二象限的点的横坐标为负数,纵坐标为正数;第三象限的点的横坐标与纵坐标都为负数;第四象限的点的横坐标为正数,纵坐标为负数.
2. 坐标轴上的点的坐标有什么特点?
x 轴上的点的横坐标为任意实数,纵坐标为 0;y轴上的点的横坐标为0,纵坐标为任意实数.
已知点P 的坐标为(a+3,b-1). (1) 若点P 在x 轴上,则b=_________; (2) 若点P 在第四象限,则a 的取值范围为 _______, b 的取值范围为 ________.
1. 分别写出图中点 A、B、 C 的坐标.
解:A (4,5), B (-5,-3), C (3,-4).
2. 在平面直角坐标系中画出下列各点, 并指出它们分别在第几象限. A (2,4), B (-2.5,3), C (-3,-2), D (1.5,-3.5).
解:如图所示点A 在第一象限,点 B 在第二象限,点C在第三象限,点 D在第四象限.
平面直角坐标系的三要素: (1) 两条数轴; (2) 互相告直; (3) 公共原点.
2. 第一、二、三、四象限内点的坐标的符号依次 为(+,+),(-,+),(-,-),(+,-).
3.x轴上的点纵坐标为0,y轴上的点横坐标为0.
4. 建立坐标系常用的方法有: (1)以图形上的某已知点或线段的中点为原点; (2)以图形上某线段所在直线为x 轴(或y 轴); (3)利用图形的轴对称性以对称轴为x 轴(或y 轴).
数学苏科版(2024)5.2 平面直角坐标系优质ppt课件: 这是一份数学苏科版(2024)<a href="/sx/tb_c100316_t3/?tag_id=26" target="_blank">5.2 平面直角坐标系优质ppt课件</a>,共31页。PPT课件主要包含了学习目标,思考与探索,尝试交流,-85,-111,-8-3,-12-8,3-6,例题讲解,讨论交流等内容,欢迎下载使用。
苏科版(2024)八年级上册5.2 平面直角坐标系获奖ppt课件: 这是一份苏科版(2024)八年级上册<a href="/sx/tb_c100316_t3/?tag_id=26" target="_blank">5.2 平面直角坐标系获奖ppt课件</a>,共36页。PPT课件主要包含了学习目标,第四象限,第一象限,第二象限,第三象限,知识回顾,新知探索,A′-35,B′-10,C′-50等内容,欢迎下载使用。
初中数学苏科版(2024)八年级上册第五章 平面直角坐标系5.2 平面直角坐标系公开课课件ppt: 这是一份初中数学苏科版(2024)八年级上册<a href="/sx/tb_c100316_t3/?tag_id=26" target="_blank">第五章 平面直角坐标系5.2 平面直角坐标系公开课课件ppt</a>,共27页。PPT课件主要包含了学习目标,知识回顾,尝试交流,向右为正方向,向上为正方向,两轴的交点O是原点,概念学习,探索交流,例题讲解,坐标平面上的点等内容,欢迎下载使用。













