人教版（2024）七年级上册1.2.4 绝对值教案

这是一份人教版（2024）七年级上册1.2.4 绝对值教案，共5页。教案主要包含了问题引入，剖析概念，新知运用，深入理解等内容，欢迎下载使用。
课程基本信息
课例编号
2020QJ07SXRJ008
学科
数学
年级
七
学期
秋季
课题
1.2.4绝对值一
教科书
书名：义务教育教科书数学七年级上册
出版社：人民教育出版社 出版日期：2019 年7 月
教学人员
姓名
单位
授课教师
史方圆
北京市第十三中学分校
指导教师
教学目标
教学目标：从数和形两方面理解绝对值的意义，会求有理数的绝对值；
教学重点：求有理数的绝对值.
教学难点：绝对值的概念.
教学过程
时间
教学环节
主要师生活动
一、问题引入
二、剖析概念
三、新知运用
四、深入理解
四、总结反思：
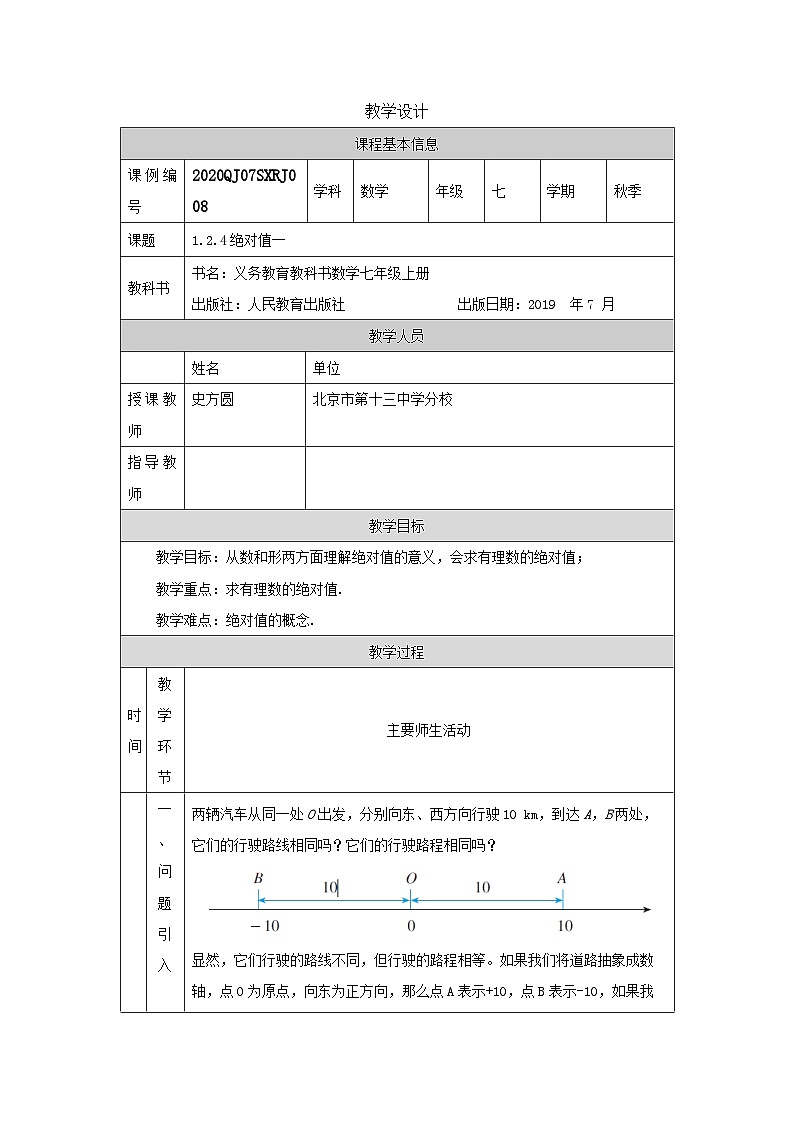
两辆汽车从同一处O出发，分别向东、西方向行驶10 km，到达A，B两处，它们的行驶路线相同吗？它们的行驶路程相同吗？
显然，它们行驶的路线不同，但行驶的路程相等。如果我们将道路抽象成数轴，点O为原点，向东为正方向，那么点A表示+10，点B表示-10，如果我们不考虑方向，只考虑路程，即点A与点B到原点O的距离都是10，这个距离就是我们这节课要学习的概念：绝对值。
一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，用这样的符号来表示，记作a。
上图中，点A与点B分别表示10和-10，它们与原点的距离都是10个单位长度，所以10和-10的绝对值都是10，即10=10，-10=10。再看上图，点O表示的数是0，那么0的绝对值等于多少呢？由于点O是原点，它与原点距离是0，所以0的绝对值等于0，即|0|=0.
现在请同学们用刚刚学习的绝对值的概念，尝试完成下面的练习。
练习 写出下列各数的绝对值。
6，-8，-3.9，52，-211, 100, 0
解：因为6在原点右侧,到原点的距离是6个单位长度,所以6的绝对值是6，即|6|=6;-8在原点左侧,到原点的距离是8个单位长度,所以-8的绝对值是8，|-8|=8;
同理可得,-3.9的绝对值是3.9 ；52的绝对值是52 ;-211的绝对值是211 ;100的绝对值是100;0的绝对值是0。请同学们尝试自己用符号语言来描述这四个绝对值。
上述各数的绝对值，与原数有什么关系？
首先，|6|=6，发现正数6的绝对值等于它本身。|52|=52，正数52的绝对值等于它本身；|100|=100，正数100的绝对值等于它本身，由此我可以得出结论：一个正数的绝对值是它本身。
其次，我们再来看：|-8|=8，它表明-8的绝对值是8，根据上节课学习的知识，我们知道8和-8是互为相反数的，所以我们得到结论：-8的绝对值是它的相反数8，类似的，因为|-3.9|=3.9，所以-3.9的绝对值是它的相反数3.9；因为|-211|=211，所以-211的绝对值是它的相反数211，由此我可以得出结论：一个负数的绝对值是它的相反数。正数与负数我们都考虑完了，还差谁呢？对，还有0.我们看到：0的绝对值是0。
由于有理数分为正数，负数和0，结合数轴，我们就可以得到如下结论：
（1）一个正数的绝对值是它本身；
（2）一个负数的绝对值是它的相反数；
（3）0的绝对值是0.
符号表示：
例1.计算：
（1）|-125|；（2）|+23|；（3）|-3.5|；（4）|23|；（5）|-32|；（6）|0|
按照求一个有理数的绝对值的方法，我们知道要求一个数的绝对值，首先需要判断这个数是正数，负数还是0，然后再按照这个方法具体求就可以了。
解：（1）-125是负数，它的绝对值应是它的相反数，所以|-125|=-（-125）=125；
（2）+23是正数，它的绝对值是它本身，所以|+23|=23；
（3）-3.5是负数，它的绝对值应是它的相反数， |-3.5|=-(-3.5)=3.5
（4）|23|=23 ；（5）|-32|=-（-32）=32；（6）|0|=0
通过上面的练习，请同学们思考下面的问题：
（1）一个数的绝对值会是负数吗？为什么？
比如说有没有绝对值等于－2的数？显然没有，因为距离不能是负数；
同样因为距离不能为负，所以没有一个数的绝对值是负的。
（2）不论有理数a取何值，它的绝对值总是什么数？
绝对值的性质：有理数a的绝对值总是非负数。
符号表示：|a|≥0
（3）互为相反数的两个数的绝对值有什么关系？
表示一对相反数的两个点虽然分别在原点两侧，但它们到原点的距离是相等的．所以互为相反数的两个数的绝对值相等．
例2. 判断下列说法是否正确：
（1）符号相反的数互为相反数；（×）
（2）一个数的绝对值越大，表示它的点在数轴上越靠右；（×）
（3）一个数的绝对值越大，表示它的点在数轴上离原点越远。（√）
（4）当a≠0时，|a|总是大于0。（√）
例3. 判断下列各式是否正确：
（1）|5|=|-5|；（2）-|5|=|-5|；
现在，我们比较熟悉绝对值的概念了，请同学们先思考，再回答下面的问题：
绝对值等于它本身的数有哪些？
绝对值等于它本身的数包含正数和0，正数与0我们统称为非负数，所以，绝对值等于它本身的是非负数。
（2）绝对值等于它的相反数的数有哪些？
同学们会马上说出负数，只有负数吗？其实0的绝对值也可是它的相反数，
所以，绝对值等于它的相反数是数是负数和0.
例4. 填空：
（1）若|a|=2, 则a= ±2 若|x|=|y|, 则: x = y 或 x =- y .（2）若|a|=a 则a ≥ 0; 若|a|=-a, 则a ≤ 0;
总结反思：
一、知识汇总：
1.绝对值的概念：一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作a，
2.绝对值的求法：（1）一个正数的绝对值是它本身；
（2）一个负数的绝对值是它的相反数；
（3）0的绝对值是0.
符号表示：
二、数学思想：
（1）在得到绝对值定义的过程中，借助了数轴这个工具帮助我们直观的理解绝对值定义，这体现了数形结合的思想；
（2）（在总结、概括求一个有理数的绝对值的方法时，首先需要判断这个数是正数，负数还是0，体现了分类讨论的思想；
（3）符号意识。上述两个过程我们都采用数学的符号来表示，以体现其表示数学符号的简洁性，在今后的数学学习中，我们还将会大量地用数学符号表示数学的定义、法则、结论等。