沪科版数学九上 23.2.1 《解直角三角形 》课件

这是一份沪科版数学九上 23.2.1 《解直角三角形 》课件，共25页。

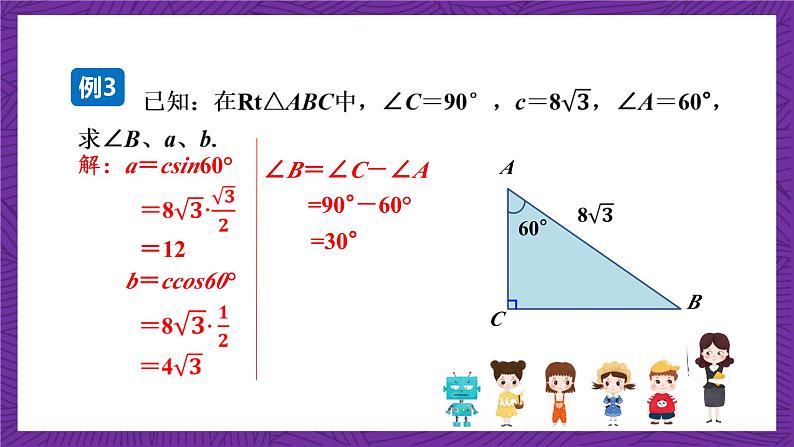
沪科版数学九年级上册使学生理解直角三角形的五个元素的关系．会运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形．直角三角形的解法．三角函数在解直角三角形中的灵活运用．教学目标直角三角形ABC中，∠C＝90°，a、b、c、∠A、∠B这五个元素间有哪些等量关系呢？(2)三边之间关系a2＋b2＝c2(勾股定理)；(3)锐角之间的关系∠A＋∠B＝90°.旧知回顾 如图，在Rt△ABC中，∠C＝90°，∠B＝42°6'，c=287.4,解这个直角三角形(精确到0.1).∴a＝c cosB＝287.4×0.7420≈213.3 . ∴b＝c sinB＝287.4×0.6704≈192.7 . ∠A＝90º－∠B＝90º－42º6′＝47º54′ . 已知一边及一锐角解直角三角形例1探究新知  在Rt△ABC中，  当∠B= 30°∠A=90°－∠B= 90º－30º＝60º.例2已知两边解直角三角形 解：a＝csin60° ＝12b＝ccos60° ∠B＝∠C－∠A=90°－60°=30° 例31.在如图的Rt△ABC中，根据AC＝2.4，斜边AB＝6，你能求出这个直角三角形的其他元素吗？解：∵AB2=AC2+BC2  ≈5.5  ∴∠A≈66°∵∠A+∠B=90°∴∠B=90°－∠A=90°－66°=24°随堂练习 解：∠B＝90°－30°＝60°         ∵∠A＝45°，∴∠B＝90°－45°＝45° 根据以上探究，解直角三角形有哪些类型？试填写下表  ∠B＝90°－∠A；a＝c·sinA，b＝c·cosA  事实上，在直角三角形的六个元素中，除直角外，如果再知道两个元素（其中至少有一个是边），这个三角形就可以确定下来，这样就可以由已知的两个元素求出其余的三个元素．直角三角形中已知的元素，求出所有未知元素的过程，叫做解直角三角形． 已知如图，在△ABC中，∠B＝45°，∠C＝60°，AB＝6，求BC的长(结果保留根号)．∴BC＝BD＋CD解：作AD⊥BC于D， AD＝AB·sinB   ＝6×sin45°      例4构造直角三角形解决问题 如图，在△ABC中，∠B=30°，∠C=45°，AC=2，求BC.解：过点 A作 AD⊥BC于D.在△ACD中，∠C=45°，AC=2， 在△ABD中，∠B=30°  例5解 如图作AB边上的高CD. 在△ABC中，∠A= 55°b=20cm，c=30cm，求三角形的面积S△ABC(精确到0.1).∵CD＝AC·sinA＝bsinA ， ∵∠A=55°b=20cmc=30cm时，   ≈245.8(cm2) 在Rt△ACD中，例6  当△ABC为钝角三角形时，如图①，∵AC=13，∴BC=BD-CD=12-5=7；∴AD=BD=ABcosB=12∴由勾股定理得CD=5例7 ∴BC的长为7或17.当△ABC为锐角三角形时，如图②，∴BC=BD+CD=12+5=17.∵AC=13，∴AD=BD=ABcosB=12∴由勾股定理得CD=5  解：作CD⊥AB于D，  ∵在Rt△CDB中，    60°1 10 D C    在Rt△BCD中，∠B＝45°，  解：∵AD是边BC上的高，AD＝12， ∴AB＝15， ∴DC＝BC－BD＝14－9＝5；解：∵E是斜边AC的中点，∴DE＝EC，∴∠EDC＝∠C，  （1）三边之间的关系a2+b2=c2（勾股定理） 在解直角三角形的过程中，一般要用到下面一些关系：（2）两锐角之间的关系∠A+∠B=90°（3）边角之间的关系      本课小结